星载飞轮双状态隔离用变刚度摩擦阻尼器

刘国勇，侯永涛，2，刘海平*，赵鹏鹏，朱冬梅

(1.北京科技大学 机械工程学院，北京 100083；2.中国兵器工业第二○八研究所， 北京 102202)

1 引 言

卫星在轨工作时，飞轮和控制力矩陀螺输出的微振动是影响其指向精度、稳定度和成像质量的主要干扰源之一[1-2]。为有效抑制微振动对星载高精度有效载荷的影响，众多学者对飞轮微振动的形成机理及其工作机制进行了大量研究[3-6]。

目前，已有很多针对星载飞轮的振动抑制研究。其中，魏展基提出了一种主动和被动隔振相结合的多段折臂梁构型的飞轮隔振平台[1]；刘海平等利用欧拉屈曲梁并联线性弹簧构建一种非线性能量阱[7]，实现了对飞轮输出微振动的宽频抑制；虞自飞等设计了一种适用于卫星飞轮等主要振源的振动抑制的隔振与吸振联合减振系统[8]，其他飞轮减隔振技术还包括多频段动力吸振器[9]、被动阻尼减振器[10]、Bipod strut被动隔振器[11]、液体阻尼隔振器[12]等。

现有减隔振装置中，虽然主动隔振的效果更好，但是由于其设计复杂，可靠性低，所以应用并不广泛[13]。被动减隔振装置虽然在轨工作阶段能有效抑制飞轮输出的微振动，但由于卫星在轨工作阶段和主动发射阶段的载荷差异较大，常规满足在轨工作阶段微振动抑制需求的减隔振装置在主动发射阶段大量级载荷激励下会产生较大的变形，引起被控制设备剧烈的摇晃[14]。为解决这个问题，目前广泛采用的办法是为每个隔振装置安装一套锁定装置，在发射阶段锁紧，入轨后解锁，这无疑会带来一系列负面影响，如附加质量大、可靠性低、系统复杂、火工解锁时瞬态冲击载荷的影响等。

变刚度摩擦阻尼器可适应不同载荷条件，通过调整其设计参数，可以同时兼顾不同的减隔振要求。在变刚度摩擦阻尼器研究方面，彭凌云提出了分别能够实现三角形滞回曲线、双旗帜滞回曲线和双线性滞回曲线的向心式摩擦阻尼器[15]；李澈设计了一种能够实现“狗骨型”滞回曲线的变刚度摩擦阻尼器[16]。但是，以上研究主要集中于建筑抗震领域。

综合上述文献关于变刚度摩擦阻尼器的设计方法，本文提出一种可以同时有效控制卫星在主动发射阶段和在轨工作阶段载荷条件下飞轮动态响应的双状态变刚度摩擦阻尼器。根据变刚度摩擦阻尼器的结构特点，建立相应的动力学模型，并分别给出力传递率和绝对位移传递率评价其不同激励条件下的减隔振性能；最后，通过物理试验验证了所建理论模型及计算结果的有效性。

2 变刚度摩擦阻尼器模型

针对星载飞轮在主动发射阶段和在轨工作阶段所受不同类型的载荷条件，提出一种变刚度摩擦阻尼器，使其在两种载荷激励下表现出不同的刚度和阻尼输出特性，可对飞轮的动态响应实现有效控制。在轨工作阶段，飞轮受自身电磁激励、机械加工精度、旋转不平衡等因素影响产生微振动，变刚度摩擦阻尼器需要具有较小的输出刚度保证有效隔振频率且利用迟滞阻尼抑制其响应，以满足微振动抑制要求。在主动发射阶段，受运载火箭点火影响传递到飞轮安装界面的动载荷较大，因而需要安装在飞轮和基础结构之间的变刚度摩擦阻尼器提供的连接刚度较大，避免其动态位移过大；此外，利用迟滞阻尼抑制其响应幅值以保护飞轮结构不发生失效甚至破坏。

综合在轨工作阶段和主动发射阶段飞轮所处力学环境条件，提出一种变刚度摩擦阻尼器如图1所示。其中，预紧弹簧具有预压缩量，小位移时输出的摩擦阻尼力恒定；当位移增大，端盖将限制定位挡板的移动，压缩弹簧被压缩，从而输出摩擦力也增加，位移越大，摩擦阻尼力越大。加载时，输出力为摩擦阻尼力与弹簧恢复力之和；卸载时，输出力为压缩弹簧恢复力与摩擦阻尼力之差。

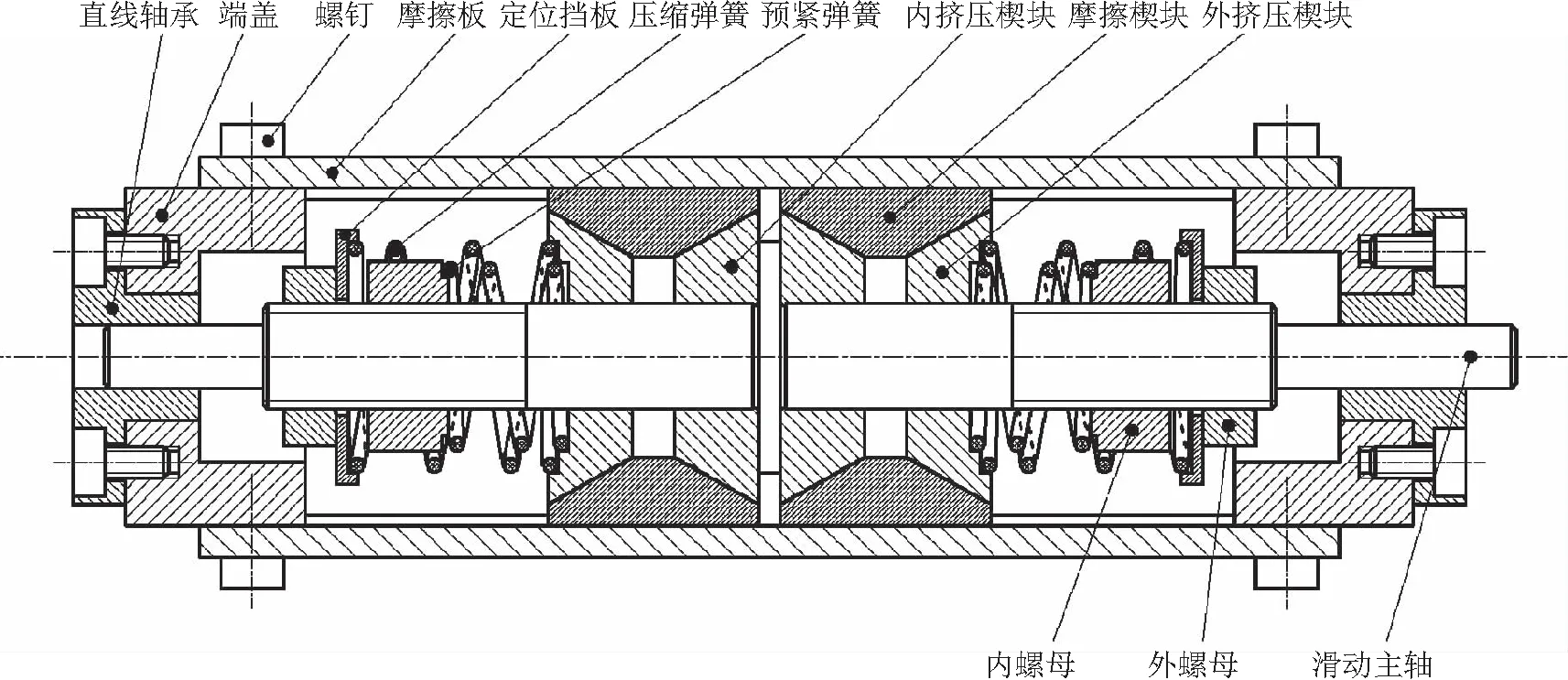
图1 变刚度摩擦阻尼器结构示意图

变刚度摩擦阻尼器的滞回特性曲线，也称为“双尾翼”型滞回曲线如图2所示。其中，u1为摩擦阻尼器平直段位移，um为最大位移；k1为上坡段刚度系数，k3为下坡段刚度系数，k0为过渡刚度系数；f0为起滑力，f1为上坡段最大出力。

在轨工作阶段，飞轮输出微振动幅度较小，摩擦阻尼器的位移小于u1，迟滞阻尼较小；主动发射阶段，飞轮所受大量级动载荷影响，摩擦阻尼器位移大于u1，将进入斜坡段，随着位移增大，迟滞阻尼也随之增大，进而可以防止阻尼器滑动位移过大。

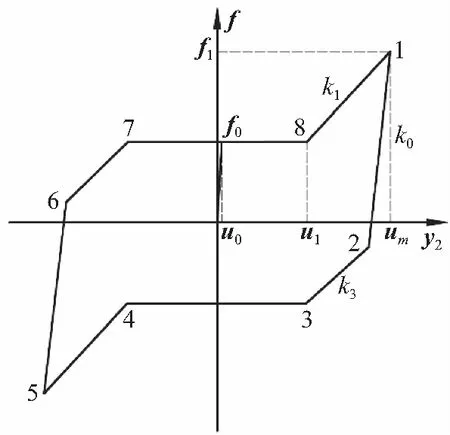
图2 滞回曲线Fig.2 Hysteresis curve

由于“双尾翼”型滞回曲线的强非线性特征，导致隔振系统动力学方程的频响结果求解困难。考虑摩擦力f关于位移具有周期性，故可将摩擦力f展开成Fourier级数形式。变刚度摩擦阻尼器位移y2用三角函数表示为：

(1)

将滞回曲线分段表示：

(2)

(3)

式中：

分段积分法进行Fourier级数展开。对式(3)中摩擦力f的表达式利用分段积分法进行一阶Fourier级数展开，可以得到式(4)：

(4)

式中α和β是关于位移幅值um的函数：

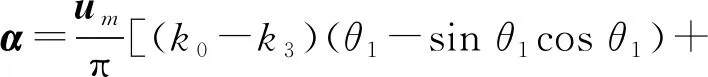
3隔振系统传递特性

3.1 在轨阶段力传递率

建立星载飞轮变刚度摩擦阻尼器系统在轨阶段力学模型如图3所示。

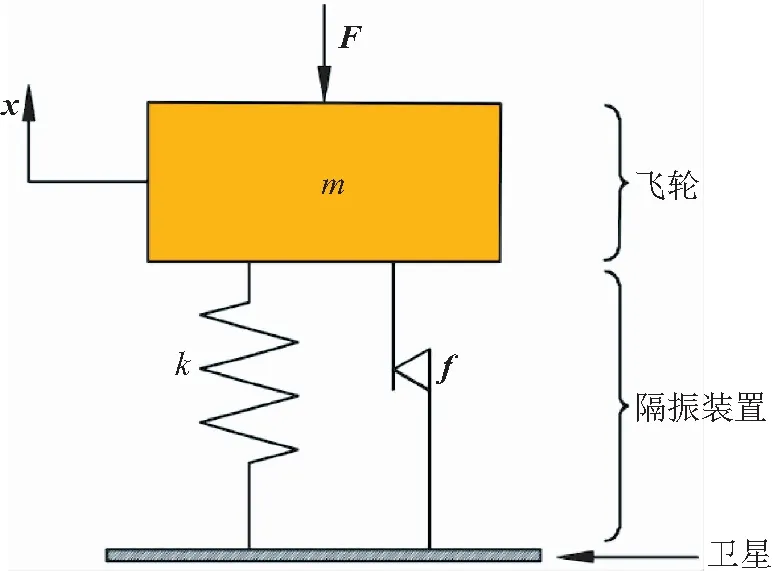
图3 在轨阶段隔振系统力学模型Fig.3 Mechanical model of isolating system on-orbit phase

其中：m为飞轮质量，k为并联弹簧刚度，x为飞轮位移，f为变刚度摩擦阻尼器输出力，F为飞轮扰振，建立隔振系统运动微分方程为：

(5)

引入以下变量：

(6)

利用谐波平衡法，假设飞轮质量位移响应为：

x=xmsin(ωt+φ).

(7)

将式(5)展开后，等式两侧谐波项sinωt和cosωt的系数相等，展开整理后得到以下方程组：

(8)

由飞轮质量传递到卫星基础的力传递率为：

(9)

根据实际飞轮参数，选定星载飞轮变刚度摩擦阻尼器各部分设计参数如表1所示。

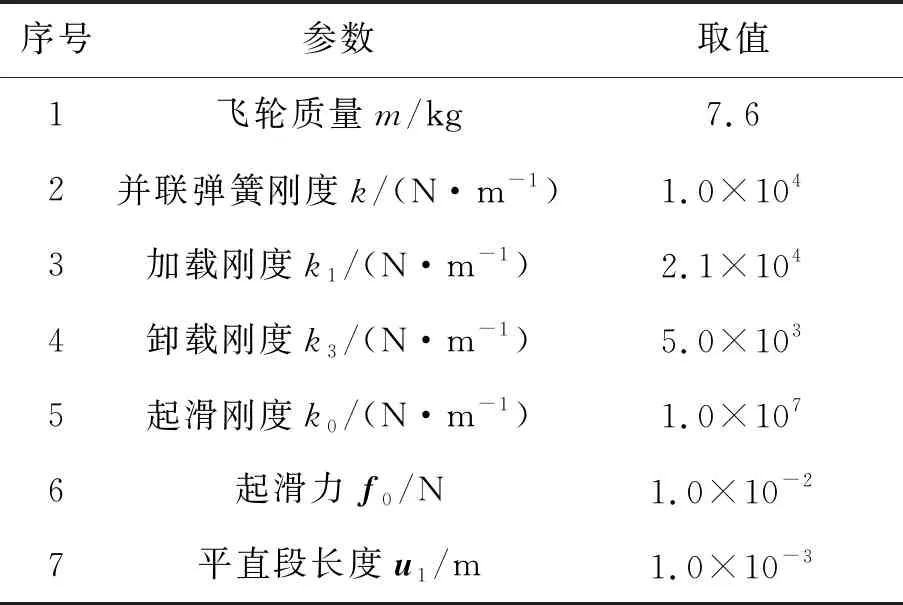
表1 设计参数值Tab.1 Design parameter values

简谐激励下得到隔振系统的力传递率曲线如图4所示。为了便于对比，图中还给出安装变刚度摩擦阻尼器前系统的力传递率曲线。

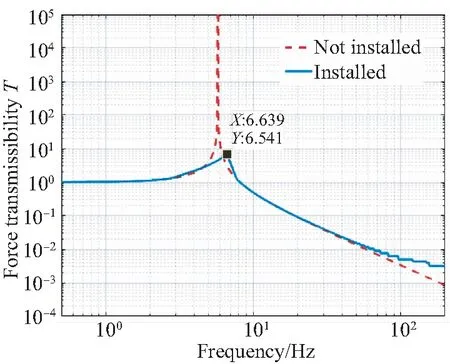
图4 力传递率曲线Fig.4 Force transmissibility curves

3.2 发射阶段绝对位移传递率

建立主动发射阶段星载飞轮变刚度摩擦阻尼器力学模型如图5所示。其中，a为发射阶段动载荷，其他参数与第3.1节在轨阶段力学模型相同。对比两种力学模型区别在于激励方式不同，在轨阶段力学模型为力激励，主动发射阶段力学模型为位移激励。建立主动发射阶段星载飞轮变刚度摩擦阻尼器运动微分方程为：

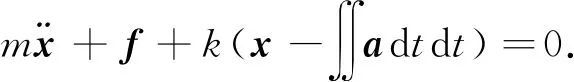
(10)

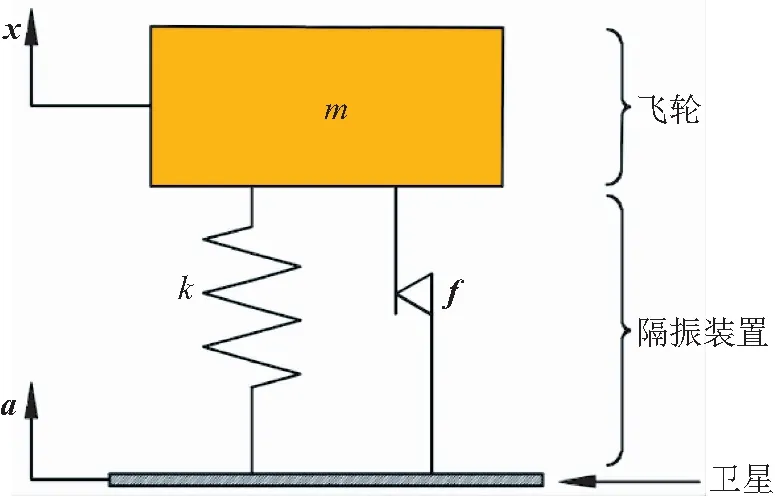
图5 发射阶段隔振系统力学模型Fig.5 Mechanical model of isolating system in launching phase

发射阶段动载荷a用正弦函数表示：

a=amsinωt.

(11)

引入以下变量：

根据谐波平衡法，假设相对位移：

y=x-u=ymsin(ωt+φ).

(12)

解得关于位移幅值ym和相位φ的非线性方程组：

(13)

由基础传递到飞轮质量的绝对位移传递率为：

(14)

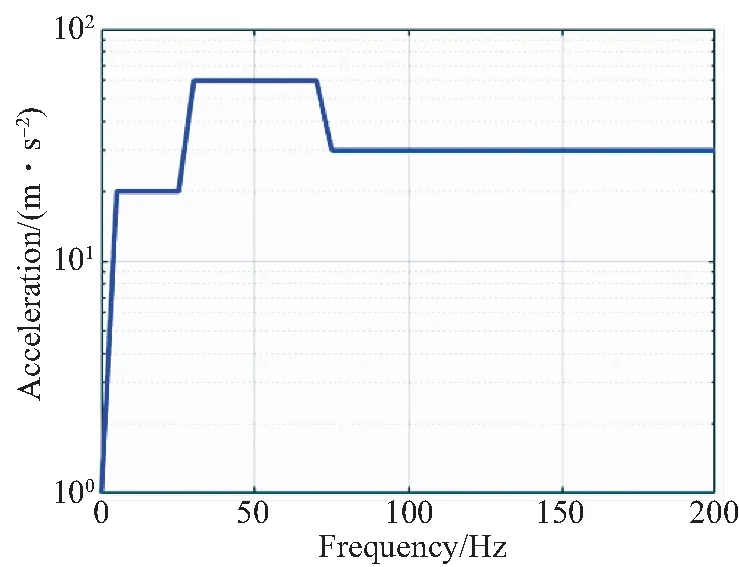
图6 发射阶段动载荷Fig.6 Dynamic load in launching phase

根据参考文献[12]给出主动发射阶段输入载荷条件如图6所示。图7给出计算得到隔振系统的绝对位移传递曲线。为了便于对比，图中给出未安装变刚度摩擦阻尼器系统的绝对位移传递曲线。

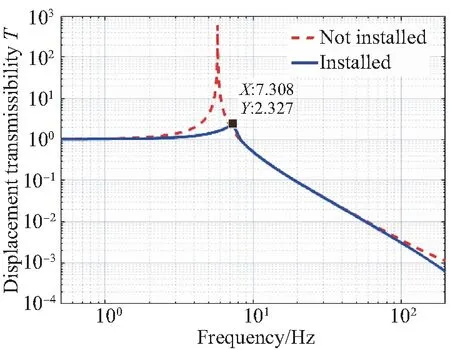
图7 绝对位移传递曲线Fig.7 Absolute displacement transmissibility curves

4 试验验证

为了验证所建理论模型和解析结果的正确性，开展并完成变刚度摩擦阻尼器力学性能测试。根据激励方式不同，分别完成基础激励和力激励传递特性测试如图8和图9所示。其中，基础激励分别采集激励位置和配重处的加速度响应，由于频域加速度响应和位移响应的传递率幅值相同，故此处可以采用实测加速度传递率评估隔振系统的绝对位移传递率特性。

图8 基础激励传递率测试状态Fig.8 Test of transmissibility under base excitation

图9 力激励传递率测试状态Fig.9 Test of transmissibility under force excitation

不同激励状态对应实测传递特性曲线如图10和图11所示。

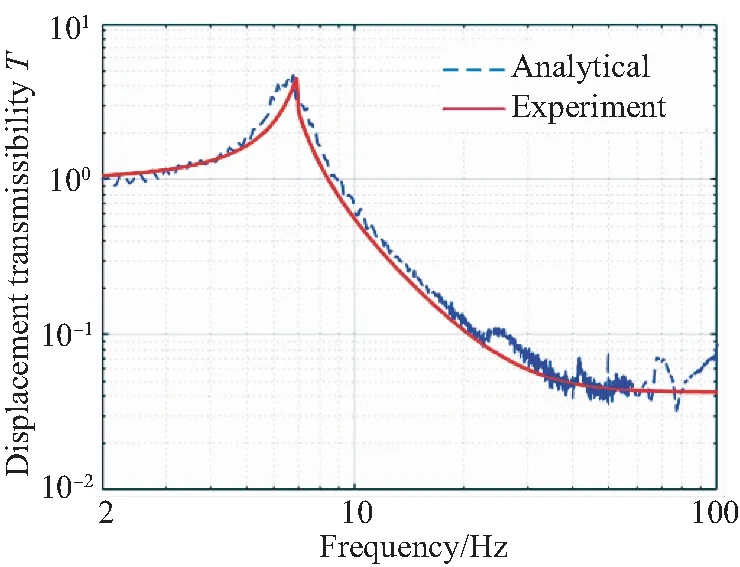
图10 绝对位移传递率曲线Fig.10 Absolute displacement transmissibility curves

图11 力传递率曲线Fig.11 Force transmissibility curves

为了便于对比，图中给出不同激励状态对应解析计算结果。由图11可见，在10 Hz以下低频范围，解析解和实测曲线一致性较好；随着频率增加，受中高频段试验件局部振动模态的影响实测曲线呈现若干谐振峰，而且减隔振效果变差；相比解析解，理论模型在中高频段的预测精度变差。

5 结 论

本文以抑制星载飞轮在轨工作阶段姿态调整过程中输出微振动和主动发射阶段由火箭经卫星本体结构传递给飞轮的动态载荷为目标，提出一种“双尾翼”型变刚度摩擦阻尼器，并进行了理论分析和试验验证。理论分析表明：安装变刚度摩擦阻尼器可有效抑制主动发射阶段和在轨工作阶段系统的动态响应，将系统绝对位移传递率和力传递率谐振频率峰值减小为6.5和2.3。结合试验实测数据证明安装变刚度摩擦阻尼器系统动力学模型有效，解析解正确。