基于分形理论的古典园林滨水岸线形态研究

徐彤 顾至欣

摘要：分形理论是对自然界不规则实体进行描述的重要方法，对研究以“师法自然”为特色的我国古典园林滨水驳岸设计有重要的启发意义。研究在阐释分形理论概念与计算方法的基础上，应用Fractalyse软件分析我国古典园林与城市公园岸线形态的计盒维数，应用SPSS19.0软件对相关变量进行相关性分析与非参数检验，发现古典园林滨水岸线计盒维数与水城面积并无显著相关性，古典园林和城市公园滨水岸线差异性也不明显。研究结论质疑了城市公园滨水岸线不如古典园林丰富生动的惯性思维，也为未来古典园林研究提供了新的思路。

关键词：分形理论;古典园林;滨水景观;驳岸;形态

中图分类号：TU986 文献标识码：A 文章编号：1674-9944（2020）03-0059-03

1 引言

风景园林水景的营造历史由来已久，世界各地园林的出现伊始几乎都伴随着“水”元素的应用，而其中中国古典园林在“治山理水”方面的成就可谓首屈一指。不论是对自然真山真水的园林化，如杭州西湖、北京颐和园昆明湖、济南大明湖等，还是对于自然山水场景在小尺度环境中的转译，如苏州拙政园、环秀山庄中的水景等，“理水”始终是中国传统园林营造中最为重要的内容之一[1]。理水之造形全在驳岸，古典园林滨水岸线的设计手法，源于自然界的湖、潭、湾、瀑等，强调对驳岸进行曲折变化的处理，因地制宜，因时制宜，用树木、建筑等稍加点缀，使湖岸景致更加优美多变，但绝对不是对自然水体进行生硬模仿或简单浓缩，而是对自然水体作抒情写意的再创造，大多取其意境的联想[2]。当下古典园林滨水岸线形态研究，多从观察者的主观视角出发，提出景与情、虚与实、动与静、因与借、真与假、有限与无限等感受体验，缺乏量化的理论分析支持，也没有办法将古典园林滨水岸线与城市公园滨水岸线进行定量比较，不利于古典园林理水研究的深入开展。研究引入曼德布罗特分形理论，尝试分析古典园林滨水岸线分形维数与水域面积的关系，同时对比分析古典园林滨水岸线与城市公园古典园林滨水岸线的形态差异，希望能为古典园林滨水岸线形态研究提供新的思路。

2 分形研究的理论基础

分形理论由数学家曼德布罗特于1973年提出的[3]，分形几何是一门以不规则自然形态为研究对象的几何学。在传统的欧式几何中，自然界中复杂实休与现象总是习惯性地被概括成常见的几何图形，而分形几何则可以直接研究它的内在规律并将其量化，是一种描述自然实体的新方法[4]。其中分形维数是对复杂物休结构的量化表达，是描述不规则线段形态的重要参数。当下分形理论已广泛应用于城乡规划的区域规划、总体规划以及建筑设计中，而且分形理论对于古典园林空间[5～7]、古典园林岸线研究也取得了一定进展[8，9]。

分形具有以非整数维形式充填空间的形态特征。通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”，即具有自相似的性质。分形理论的最基本特点是用分数维度的视角和数学方法描述和研究客观事物，也就是用分形分维的数学工具来描述研究客观事物。它跳出了一维的线、二维的面、三维的立体乃至四维时空的传统藩篱，更加趋近复杂系统的真实属性与状态描述，更加符合客观事物的多样性与复杂性。

2.1 分形维数

分形维数是量化分形体的基础，分形维数是指将一个整体划分为N个大小和形态完全相同的小图形，每个小图形的线段长度是原图形r倍。式（1）中D。代表分形维数，简称为分维，N（r）为小图形的数量;1/r为每个小图形的线段长度。分形维数是对分形体细部与层次变化的量化反映，也是本文研究滨水岸线分布特征的主要参数。

2.2 计盒维数

分形维数的计算方法较多，在对滨水岸线提取与计算中选择较为常用的计盒维数法。滨水岸线是一个部分与整休相似的线性结构，可以使用计盒维数模型提取并量化其自相似性与复杂性。计盒维数的定义提示了一种测量分形的方法。取边长为r的小盒子，把分形覆盖起来。由于分形内部有各种层次的空洞和缝隙，有些小盒子会是空的。数有多少盒子不是空的，把这个数目记为N（r）。然后缩小盒子的尺寸ε，所数得的N（r）自然要增大。在双对数坐标纸上画出In N（r）对Inr的曲线，其直线部分的斜率就是此分形对象的计盒维数[10]，公式如式（1）。

3 研究案例与方法

3.1 研究案例

以蘇州壶园、环秀山庄、留园、陆宅半园、狮子林、网师园、怡园、艺圃、拙政园等9个古典园林滨水岸线为研究对象，同时调研南京百家湖、南京莫愁湖、南京玄武湖、南京南湖、苏州金鸡湖、苏州东沙湖、苏州尹山湖、无锡蠡湖、镇江塔影湖等9个城市公园滨水岸线进行对比研究。

3.2 研究方法

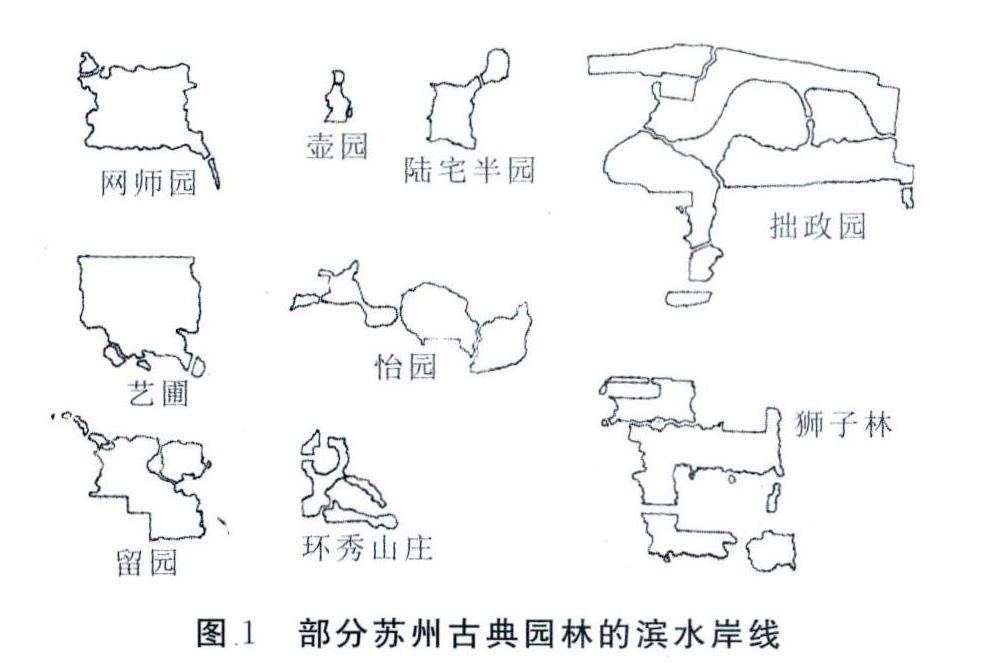
研究首先参考刘敦祯《苏州古典园林》中壶园、环秀山庄、留园、陆宅半园、狮子林、网师园、怡园、艺圃、拙政园等9个古典园林的平面图，结合实地考察修正后，利用Auto CAD软件绘制其滨水岸线，并测量其面积（图1）。同时以百度地图为底图，利用Auto CAD软件绘制南京百家湖、南京莫愁湖、南京玄武湖、南京南湖、苏州金鸡湖、苏州东沙湖、苏州尹山湖、无锡蠡湖、镇江塔影湖等9个城市公园滨水岸线。

将绘制的滨水岸线导入Fractalyse软件，运行boxanalysis，得到滨水岸线的计盒维数。研究根据滨水岸线的来源将其划分为“古典园林”和“城市公园”两种类型，将面积、计盒维数等2个变量数据分别输入SPSS19.0软件进行统计学分析。①相关性分析是研究现象之间是否存在某种依存关系的统计方法。研究对面积、计盒维数指标变化进行相关性分析，从而探讨古典园林滨水岸线形态与水域面积的关系。②独立样本T检验是检验两组非相关样本数据差异性的方法。研究将分析“古典园林”和“城市公园”两种类型滨水空间计盒维数的差异，以探究其中的规律。

4 分析结果

4.1 古典园林滨水岸线形态与水域面积相关性分析

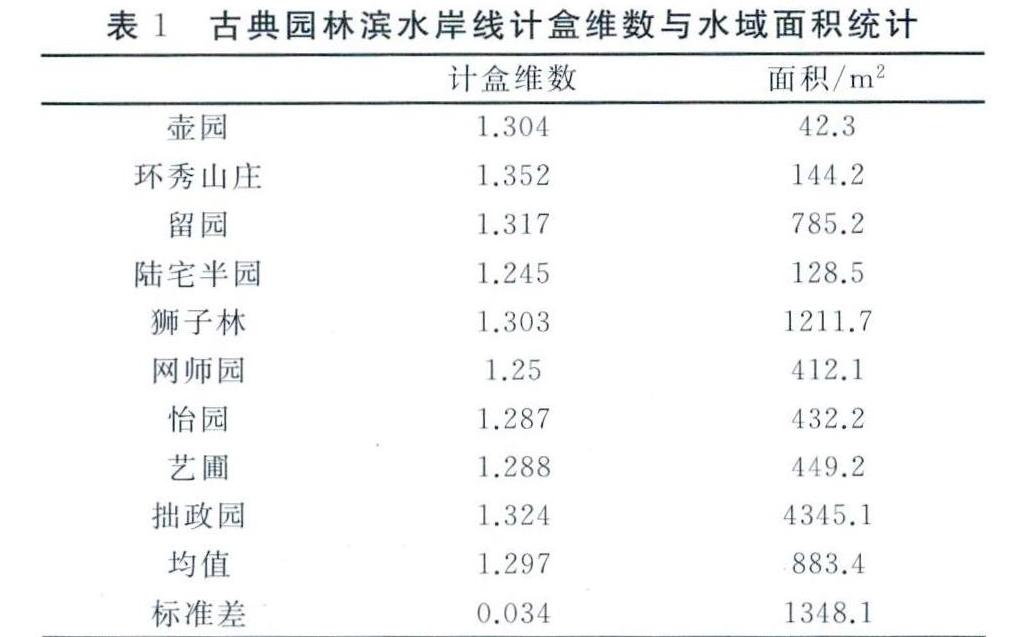
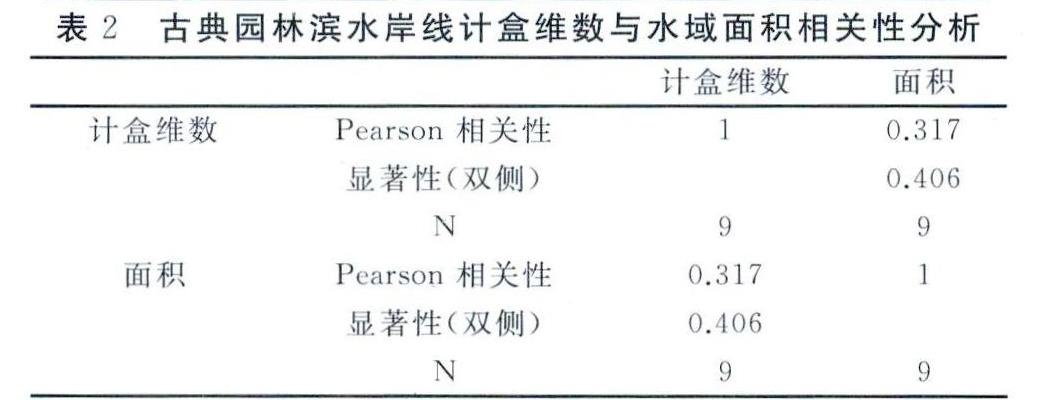
为验证古典园林滨水岸线形态与水域面积的关系，研究应用以上方法对滨水岸线计盒维数与面积进行了测量，测量表面苏州古典园林滨水岸线平均计盒维数1.30，平均面积883.39m²，古典园林滨水岸线间计盒维数差异不大，但水域面积差异较大（表1）。进而采用SPSS19.0软件进行相关性分析。设定显著性水平a=0.05，在相关性不显著的原假设下，发现古典园林滨水岸线计盒维数与水域面积的检验显著性Sig.值为0.406，大于0.05，故肯定原假设，说明两者相关性并不显著（表2）。

4.2 古典园林和城市公园滨水岸线差异性分析

首先，统计古典园林和城市公园滨水岸线的计盒维数（表3），发现古典园林滨水岸线计盒维数（1.297）略大于城市公园滨水岸线计盒维数（1.247）。其次，应用软件进行Levene检验，设定显著性水平α=0.05，在方差齐性的原假设下，计盒维数变量检验值Sig.值为0.00，小于0.05，因此认为数据不服从正态分布，对不呈正态分布的分组数据应进行Kolmogorov-Smirnov非参数检验（图2）。检验结果表明，Sig.值为0.124，大于0.05，在两组数据不存在显著差异的原假设下，故肯定原假设，认为古典园林和城市公园滨水岸线的分形特点没有显著差异。

5 结论与讨论

分形维数的基本思想是分形维数越大，图像的细节越丰富，图像的形状越不规则[11，12]。传统研究认为“小中见大”是中国古典园林的重要特色，而古典园林的驳岸设计也讲究曲折迁回，在较小的范围内形成非常丰富的景观层次与变化。李早提出古代造园家十分注重水型、岸畔的设计，“延而为溪，聚而为池”，利用水面的开合变化，形成不同水体形态的对比与交融，池岸形态丰富，有贴水石矶、亭台水榭、亲水草坡、陡崖堑路及夹涧石谷等多种变化[13]。龚志红认为传统城市公园驳岸设计过于单一化，缺乏亲切宜人、变化丰富的活动场所[14]。胡小冉认为岸线是塑造人工湖几何轮廓的决定因素，但现代城市公园的驳岸设计并没有完全继承我国古典园林设计的优良传统，部分公园滨水区岸线表现的较为呆板、僵直[15]。如果将这两种观点结合在一起，那么古典园林的水池驳岸的分形维数应该显著高于城市公园水域，而古典园林水池面积越小，驳岸边界也应该越丰富。然而，这些观点并没有被本次的调查所支持。古典园林与城市公园的水岸线分形维数没有显著差异，说明我国古典园林与城市公园的驳岸设计有着异曲同工之妙，同时我们调查的城市公园大都围绕天然湖泊设计而成，并不是我们印象中的呆板、僵直，相反很多城市公园的水岸线形式也很丰富。研究结论一方面肯定了我国的公园水景设计，另一方面也恰恰印证了我国古典园林“师法自然”，仿造天然湖泊的理水特色。

当然，本研究的研究案例有限，调查的变量也仅仅局限在面积与岸线分形维数，对比调查的分组也仅仅是古典园林与城市公园，分组与案例代表性论证仍不充分。但这种尝试却是一种有益的探索，通过分形理论来再认识我们的古典园林，发现在定性研究中难以探索的规律，或者被研究者主观印象所曲解的思想。未来，在进一步测算古典园林中的假山轮廓、天际线、建筑轮廓等要素分形维数的基础上，可以探讨其与景观美感度、游客体验等指标之间的关系，也有利于深入分析中西方园林设计差异，以期为新时期我国古典园林研究的推陈出新提供新的思路。

参考文献：

[1]张晋.可持续水设计视角下对于中国古典园林理水的几点思考[J].中国园林，2016（8）：117-122.

[2]周保良.中国古典园林水景理法及其在城市公园中的应用研究[D].邯郸：河北工程大学，2017.

[3]Mandelbrot BB.The Fractal Geometry of Nature.[M].NY：W.h.Freeman，1983：468.

[4]Arlinghaus SI.，Arlinghaus WC.The Fractal Theory of CentralPlace Geometry：a Diophantine Analysis of Fractal Generators forArbitrary L？schian Numbers[J].Geographical Analysis，1989，21（2）：103～121.

[5]Lu S.Hidden orders in Chinese gardens：Irregular fractalstructure and its generative rules[J].Environment & Planning BPlanning & Design，2010，37（6）：1076～1094..

[6]冯艳，田芃，田朝阳.中国传统园林的分形几何美学——对西方的欧氏几何美學的反叛[J].华中建筑，2016（1）：11-15..

[7]田朝阳.陈晶晶，闫一冰.中国园林的分形同构[J].华南理工大学学报（社会科学版），2015（4）：77～83.

[8]李海英.中国古典园林的分形美研究[D].哈尔滨：东北林业大学，2008.

[9]陆邵明.分形叙事视野下江南传统园林的空间复杂性解析——以醉白池为例[J].城市发展研究，2013（6）：160～165.

[10]孙博玲.分形维数（Fractal dimension）及其测量方法[J].东北林业大学学报，2004，32（3）：116-119.

[11]蒋书文，姜斌，李燕，等.磨损表面形貌的三维分形维数计算[J].摩擦学学报，2003，23（6）：533～536..

[12]杨彦从，彭瑞东，周宏伟.三维空间数字图像的分形维数计算方法[J].中国矿业大学学报，2009（2）：251-258.

[13]李早.中国古典园林理水的现代启思[J].中国园林，2004，20（12）：33～36..

[14]龚志红.城市公园人工湖驳岸设计研究[D].长沙：中南大学，2012.

[15]胡小冉.城市综合公园人工湖驳岸及亲水景观的改造与设计[D].杨凌：西北农林科技大学，2016.

收稿日期;2019-12-30

作者简介：徐彤（1987-），女，工程师，研究方向为风景园林规划设计。

通讯作者：顾至欣（1985-），男，副教授，研究方向为风景园林规划设计。