车车通信CBTC系统区间追踪间隔研究
2020-08-03胡云卿耿宏亮
郑 艺,胡云卿,耿宏亮,孙 野,沈 涛,孙 可
(1. 湖南中车时代通信信号有限公司 北京分公司, 北京 100079;2. 中车株洲电力机车研究所有限公司,湖南 株洲 412001)
0 引言
国内城市轨道交通信号系统技术在不断更新,从传统的基于通信的列车自动控制(communication based train control,CBTC)系统[1]发展到互联互通CBTC系统[2],再发展为全自动无人驾驶CBTC系统[3]。随着通信技术和控制技术的发展,基于车车通信的CBTC系统逐渐发展,近几年,部分列控系统供应商及相关研究机构开始对基于车车通信的CBTC系统进行相关研究设计[4-8]并取得了显著成果。
城市轨道交通信号系统中的列车追踪间隔模型一直是信号领域的研究热点之一,如何优化列车追踪间隔更是研究的重点和难点问题之一。文献[9]提出了通过优化紧急制动距离、优化司机在站台确认信号的时间和优化紧急保障制动率这3种措施来优化列车追踪间隔。文献[10]提出了基于调整站台限速的列车追踪间隔优化算法。文献[11]提出了通信延迟条件下的CBTC列车追踪间隔非线性规划计算方法。
车车通信CBTC系统具有扁平化架构、低时延、接口少等特点,为优化列车追踪间隔提供了新的可能性。本文首先对车车通信CBTC系统的列车追踪原理以及区间追踪间隔时间进行概述,介绍当前工程应用上的经典列车区间追踪间隔模型,继而提出了一种基于车车通信CBTC系统的列车追踪间隔模型并进行仿真分析。
1 车车通信CBTC系统列车追踪原理
在车车通信CBTC系统中,由于前行列车与后续列车建立有直接的“车-车”无线通信链路,前行列车通过该无线通信链路将本列车的当前位置等关键信息传输给后续列车,后续列车根据收到的前行列车数据进行移动授权的计算,以此保证在最不利情况下也不会发生追尾事故。基于车车通信的CBTC系统列车追踪原理示意如图1所示。
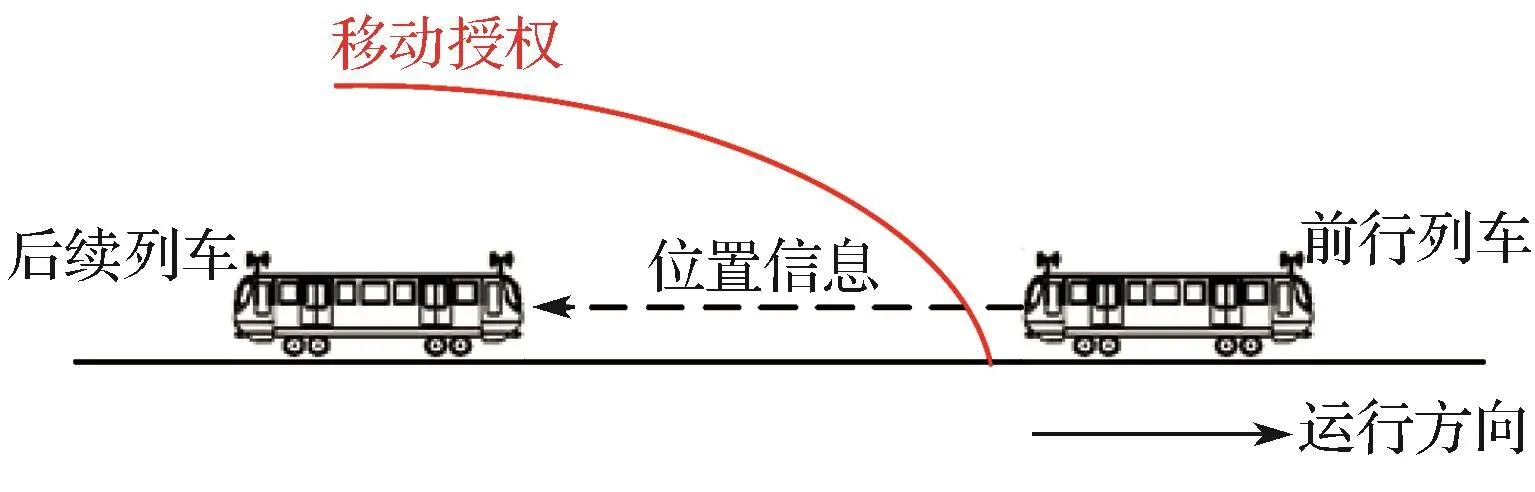
图1 车车通信CBTC系统列车追踪原理Fig.1 Train tracking principle of CBTC system based on train-train communication
列车追踪间隔是指前行列车与后续列车通过同一位置时的时间间隔,是评价CBTC系统的重要性能指标之一。追踪间隔的大小影响轨道交通系统的列车运营密度,直接影响着运输效率。列车追踪间隔主要分为正线追踪间隔和折返追踪间隔两类,其中正线追踪间隔又分为区间追踪间隔和站台区域追踪间隔。本文主要讨论基于车车通信的CBTC系统的区间追踪间隔时间。
2 列车区间追踪间隔模型优化
当前工程化过程中常用的追踪间隔模型主要为绝对追踪模式的追踪间隔模型。该模型只关注前车当前时刻的位置信息,不考虑前车的制动距离。绝对追踪模式示意如图2所示。
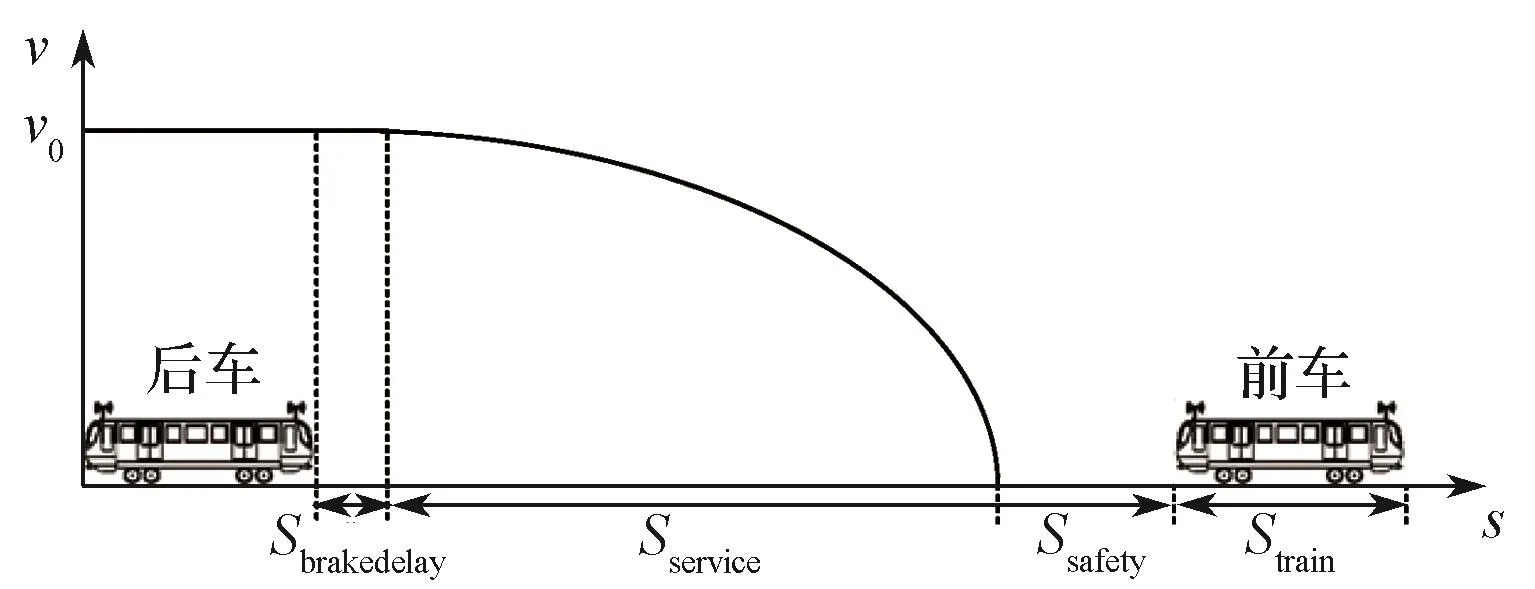
图2 列车绝对追踪模式示意Fig.2 Schematic diagram of train absolute tracking mode
绝对追踪模式的追踪间隔距离Sheadway可以表示为

式中:Sbrakedelay——制动施加延迟的过程中后车走行距离;Sservice——后车实际施加制动后由初始速度v0制动到零速的行驶距离;Ssafety——后车目标停车点与前车后端之间的安全距离;Strain——前车长度。
若v0(s)表示追踪列车在追踪过程中任意位置上的自动驾驶速度,对追踪距离取微元ds,且经过ds的距离耗时为dt,则有


绝对追踪模式的列车区间追踪间隔模型只考虑了当前时刻的前车位置信息,即假设前车在区间运行状态为静止,但是在正常运营情况下,前车一般为运动状态;同时,追踪列车得到的前车位置信息存在通信延迟,即追踪列车获取到的前车位置是发生通信延迟前的前车位置,这两个因素使采用绝对追踪间隔模型的列控系统运输效率较低。为此,针对车车通信CBTC系统,将从这两个方面进行优化。
2.1 考虑前车运行状态的追踪模型优化
车车通信CBTC系统可以直接通过车车通信实时获取前车的运行状态信息,因此可以通过考虑前车运动状态,进一步缩短追踪间隔距离。优化后的追踪模型原理示意如图3所示,其中黑色车辆表示制动前的位置,蓝色车辆表示制动到零速后列车位置。
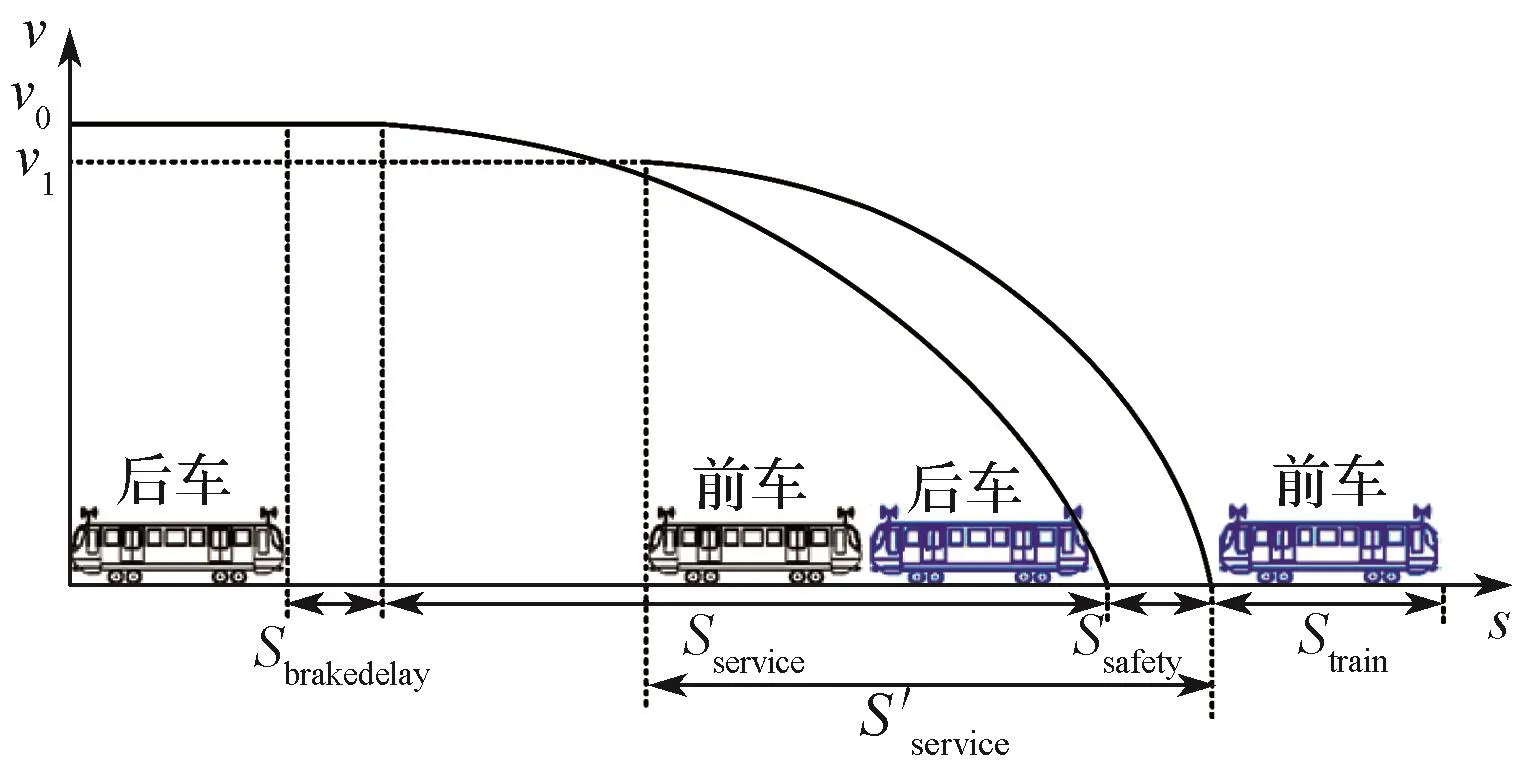
图3 考虑前车运行状态的列车追踪模型示意Fig.3 Schematic diagram of train tracking model considering running state of the preceding vehicle
列车区间追踪间隔距离将被修正为

式中:S′service——前车由初始速度v1制动到零速的制动距离。
假设前后两列车的制动减速度在制动过程中保持恒定,则Sservice和S′service可以分别表示为


式中:v0——后车施加制动前的初始速度;v1——前车施加制动前的初始速度;a0——后车的制动减速度;a1——前车的制动减速度。
考虑前车运动状态的追踪间隔模型的追踪间隔时间计算公式同式(3),其中Sheadway经过修正后其值更小,列车区间追踪间隔时间因此降低。
2.2 考虑通信时延的追踪模型优化
通信延迟在CBTC系统中不可避免,这就造成了追踪列车得到的前车运行状态信息是通信延迟前的,在收到信息的时刻前车运行状态已经发生了改变,从而影响了线路运行效率。优化后的考虑通信时延的列车追踪间隔模型示意如图4所示,其中灰色列车表示追踪列车获得的通信时延发生后的前车位置,此刻前车实际应处于图中的黑色前车所示的位置,前车当前速度用v1表示。

图4 考虑通信延迟的列车追踪模型示意Fig.4 Schematic diagram of train tracking model considering communication delay
考虑通信延迟后的列车区间追踪间隔距离计算公式被修正为

式中:Sdelay——通信时延的时间内前车行驶的距离。
假设通信时延取值为Δt,则在通信时延Δt的时间内,前车行驶距离Sdelay为

式(8)中,v1(t)表示前行列车在追踪过程中任意时刻的自动驾驶速度,通过积分可得通信时延过程中列车的运行距离。
3 仿真结果及分析
根据上文的研究分析,通过对经典的区间列车追踪间隔模型进行优化,研究设计了一种新的列车区间追踪间隔模型。通过对传统追踪间隔模型和本文提出的追踪间隔模型的差异进行比较及定性分析得出,采用该模型可以进一步减少区间列车追踪间隔时间,提高线路运营效率。
采用Matlab仿真软件分别对传统列车区间追踪间隔模型和本文提出的列车区间追踪间隔模型进行仿真,并且对仿真数据进行定性和定量分析,相关参数如表1所示。

表1 系统仿真参数Tab.1 System simulation parameters
图5示出目前广泛使用的绝对追踪模型的区间列车追踪间隔时间模型仿真结果。追踪间隔时间与列车运行速度的关系类似于反抛物线,当速度过低或较高时,追踪间隔时间都较大。可以看到,当列车以45 km/h左右的速度运行时,列车的追踪间隔时间约为29.5 s,达到最优值。
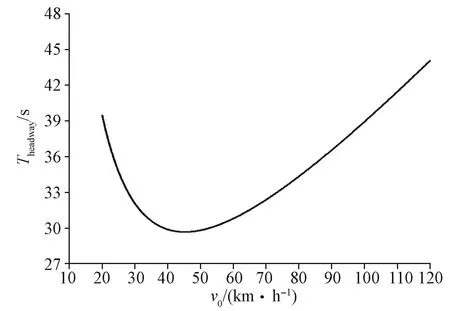
图5 绝对追踪模型的区间追踪间隔曲线Fig.5 Interstation tracking interval curve of the absolute tracking model
图6 示出本文提出的车车通信CBTC系统区间列车追踪间隔模型的仿真结果。可以看出,前行列车与追踪列车速度相等时,区间追踪间隔最优;若前行列车速度低于追踪列车速度时,追踪间隔时间会增大,例如,当追踪列车速度为50 km/h时,前列车分别以50 km/h,40 km/h,37.5 km/h,30 km/h这4种速度值运行时,追踪间隔时间分别为14.6 s, 17.7 s, 18.5 s, 20.9 s。因此保证运营列车在区间时速度相近,有利于缩短追踪间隔时间。
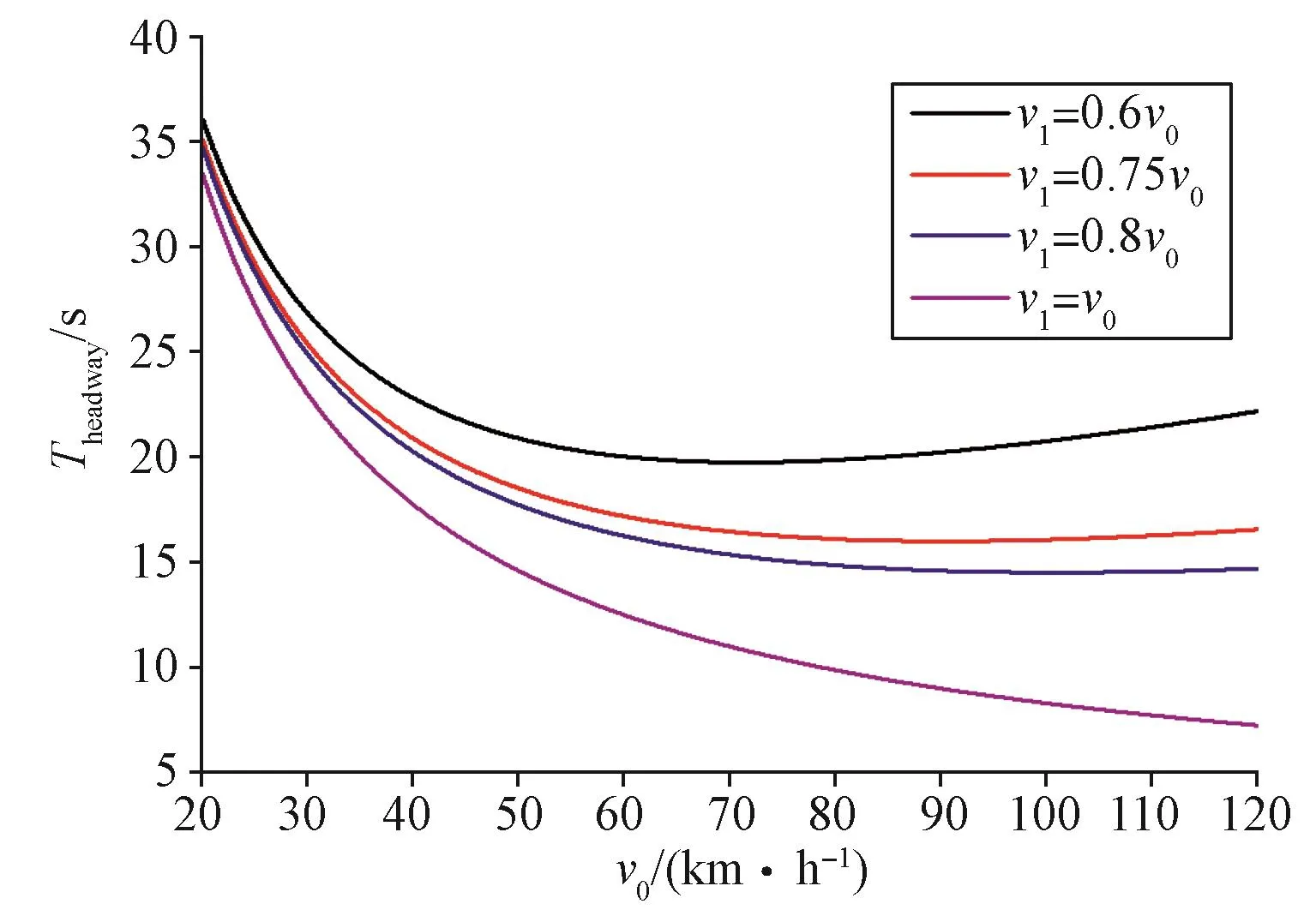
图6 车车通信CBTC系统区间追踪间隔曲线Fig.6 Interstation tracking interval curve of CBTC system based on train-train communication
通过比较图5与图6,可以看出本文提出的区间追踪间隔模型在相同条件下,能有效缩短列车追踪间隔时间,从而提升线路运行效率。
4 结语
本文在基于车车通信的CBTC系统基础上,针对该系统的追踪原理,提出了一种考虑前行列车运行状态和通信时延的区间追踪间隔模型,并通过计算机仿真的方法,详细分析了区间追踪间隔。仿真结果表明,该模型能够有效缩短列车追踪间隔时间,提升系统运输效率。后续还需要深入研究基于车车通信的列车编队运行、虚拟重联的列车追踪间隔模型,这将会更大程度地缩短追踪时间、提升线路运能。
