一种基于三阶角度观测器的旋转变压器解码算法

余 康，郭志大，陈 磊，陈建明，周 成，刘 旺

（株洲中车时代电气股份有限公司， 湖南 株洲 412001）

0 引言

旋转变压器（简称“旋变”）是一种电磁式传感器，可以精确测量转子位置。与光学编码器相比，旋变具有坚固耐用、抗振动、适用温度范围广等优点，被广泛应用于新能源汽车的电驱动系统中。旋变的信号解码电路复杂，一般需要采用价格昂贵的专用芯片（如AD2S1200，AD2S1210等）进行解码，成本高且电路设计复杂，难以被广泛用于对成本有严格要求的场合[1]。本文提出一种旋变软件解码方式，其能省去昂贵的解码芯片，同时具有较高的解码精度和较好的动态响应性能，在新能源汽车领域具有非常好的应用前景。

1 旋变软件解码

1.1 旋变工作原理

新能源汽车电驱动系统通常采用旋变来获取电机转子角度位置。旋变是一种绝对角度信号传感器，目前常用的旋变，其一次侧绕组和二次侧绕组均位于定子上，两个二次侧定子绕组机械错位90°。旋变转子的特殊设计使得二次侧所耦合的电压随转轴角位置的变化而发生正弦变化。旋变工作原理如图1所示。图中，R1和R2表示旋变激励信号输入端；S1和 S3表示旋变正弦输出端； S2和S4表示旋变余弦输出端；θ为转子角度。

图1 旋变原理示意Fig. 1 Schematic diagram of resolver

旋变激励信号为

旋变两个定子绕组输出信号为

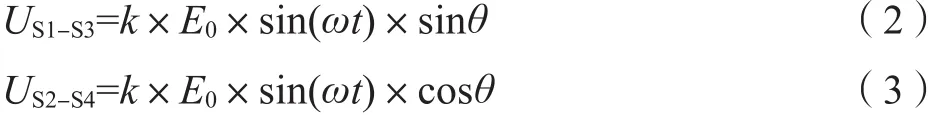
式中：k——旋变电压比；E0——励磁电压幅值；ω——激励信号角频率。

旋变激励信号与两个定子绕组输出信号的关系如图2所示。

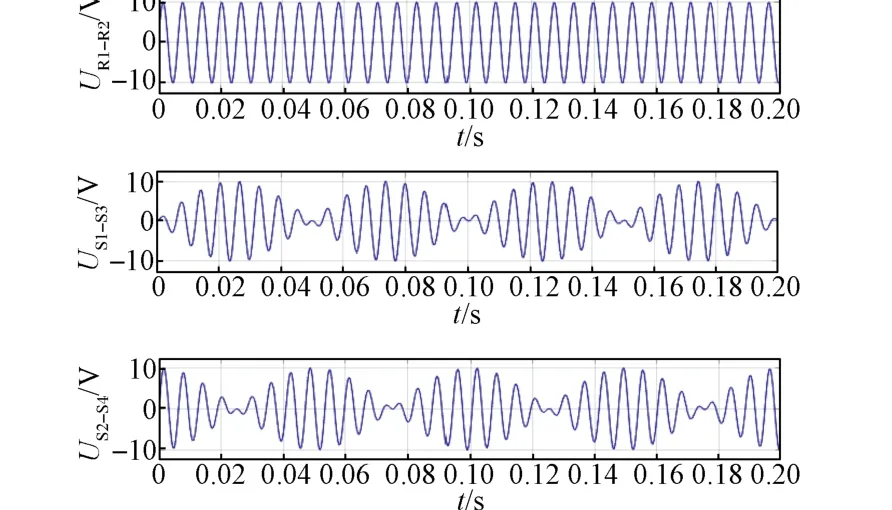
图2 旋变输入、输出信号Fig. 2 Input and output signals of resolver

1.2 旋变软件解码原理

旋变输出信号中既包含转子角度信息又有激励信号高频分量信息。为解码转子轴角信息，滤除激励信号高频分量信息，采取如下方法：以激励信号频率作为采样频率、在输出信号中激励信号分量幅值最大的时刻进行采样，即sin(ωt)=1，则采样后的旋变输出信号为

式中：Uadc1——旋变正弦输出端采样时刻信号；Uadc2——旋变余弦输出端采样时刻信号。

可见，采样后的旋变信号只包含转子角度信息。如此即可采用微控制单元（microcontroller unit, MCU）对旋变输出信号进行采样，并将采样后的正、余弦信号输入至角度跟踪观测器中，由角度跟踪观测器得到角度和速度信息，从而实现旋变的软件解码。

1.3 旋变软件解码系统设计

旋变软件解码系统结构如图3所示。MCU的PWM引脚输出10 kHz方波信号，经硬件电路调理放大后变为10 kHz正弦波输入到旋变的激励端。MCU的ADC1和ADC2通道对旋变输出信号进行采样并将采样值输送至角度跟踪观测器中，通过角度跟踪观测器得到平滑的角度与速度信息。

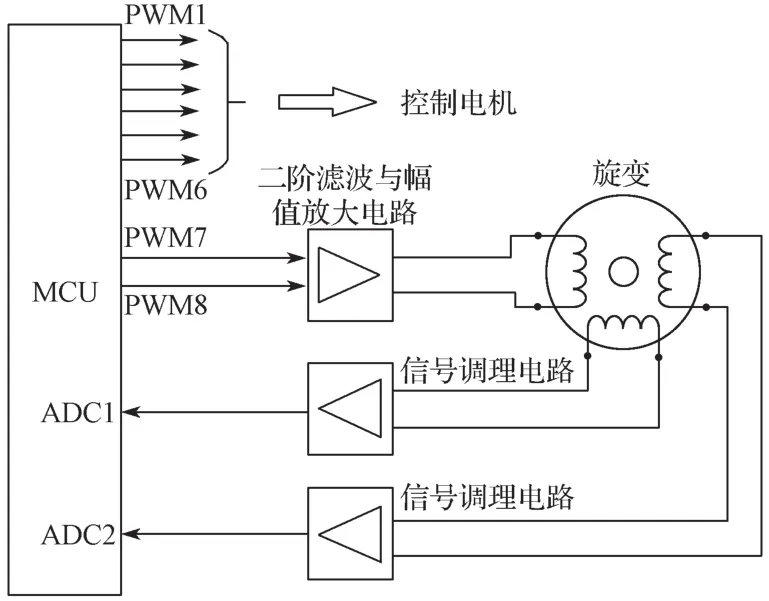
图3 旋变软件解码系统Fig. 3 Software-decoding system of resolver

为了补偿硬件电路滤波带来的延时，包括旋变激励信号滤波延时以及旋变输出信号调理带来的延时，以确保在sin(ωt)=1时刻进行采样，每次上电初始化过程中需要对激励信号的相位进行校准，以保证采样时刻的正确。具体方法如下：AD的采样时刻保持不变，通过调整激励信号的PWM相位进行校准；每微调一次激励信号的PWM相位，记录下ADC1和ADC2的采样值；对激励信号PWM相位进行N次微调，找出N次微调中ADC1与ADC2平方和最大时所对应的相位，将该相位作为后续激励信号PWM的相位即可。激励信号PWM相位校准过程如图4所示，其中i用于记录相位调整的次数。

图4 PWM相位校准过程Fig. 4 PWM phase calibration process

正常情况下，旋变输出信号幅值相等，相位相差90°， ADC1和ADC2采样值的平方和为常数，因此可以利用此特性对旋变信号进行故障监控。将旋变信号正常幅值的平方和作为标定量存入到MCU中并与旋变信号采样值平方和进行对比，从而实现旋变信号的故障检测[2]。比如，旋变的某一路输出信号出现断线故障，则对应通道的ADC采样值变为0，两个ADC采样值的平方和出现周期波动，当该值小于某一阈值时，则判断为断线故障。断线故障阈值的设置需从最大故障判断时间和故障判断灵敏度这两个方面进行综合考虑。

2 三阶角度跟踪观测器解码算法

采样后的旋变正弦和余弦信号可直接通过反正切计算得到角度信息，再通过角度微分运算得到速度信息。由于旋变输出信号中一般含有噪声和高次谐波，直接反正切计算得到的角度值波动很大，不可被直接使用。为了得到平滑可用的角度信息，一般采用角度跟踪观测器来解算角度和速度信息[1,3-4]。目前主流的旋变解码专用芯片（如AD2S1200）采用二阶角度跟踪观测器来解算角度与速度信息[5]。二阶角度观测算法在加速度响应上存在稳态误差，因此在电机快速加减速时存在误差较大的现象。鉴于此，本文设计了一种三阶角度观测器来解算角度与速度信息，其优点是加速度响应稳态误差为零。

2.1 原理分析

三阶角度跟踪观测器原理如图5所示[6]。当跟踪角度Ψ与实际角度θ偏差ζ很小时，存在ζ=sin(θ-Ψ)≈θ-Ψ。

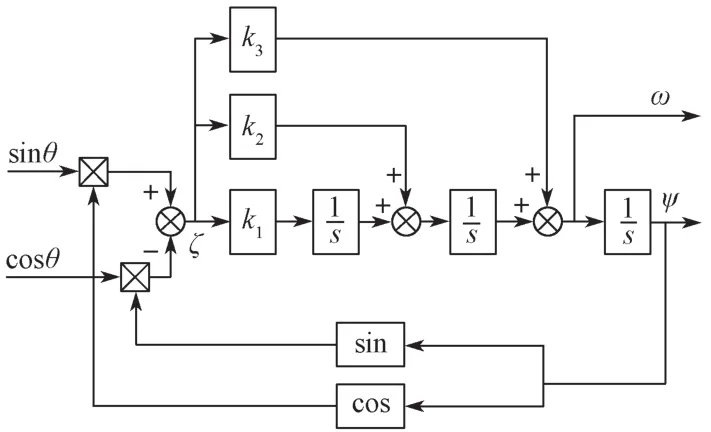
图5 三阶角度跟踪观测器原理Fig. 5 Principle of third-order angle tracking observer

角度跟踪观测器的闭环传递函数为

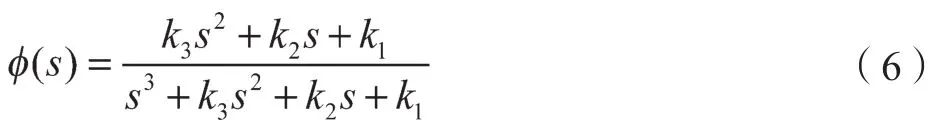
式中：k1,k2,k3——角度跟踪观测器的调节参数。

由劳斯-赫尔维茨稳定判据可得，该三阶系统稳定的充要条件为

该闭环传递函数存在3个极点。在系统稳定的前提下，3个极点要么为3个负实数极点，要么是一个负实数极点和一负实部的共轭复数极点对。考虑一般情形，将闭环系统传递函数写成如下标准形式：

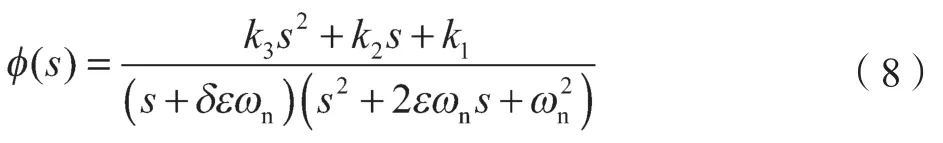
式中：δ——负实极点位置调节系数；ε——阻尼比；ωn——固有频率。

由此可得

将式（9）～式（11）代入式（7），可得：当δ＞0且ε＞0时，系统都是稳定的。

2.2 参数选择与优化

利用参数δ可调节负实数极点到虚轴的距离。一般将系统的主导极点配置为负实部的共轭极点对，则负实数极点与虚轴的距离应远大于共轭极点对到虚轴的距离，因此一般取δ≥10。通过合理地配置零极点位置，可获得最佳的系统性能。图6给出了不同参数对阶跃响应的影响情况。可以看出，超调量与调节时间之间存在矛盾，因此角度跟踪观测器参数取值需要综合考虑调节时间与超调量。

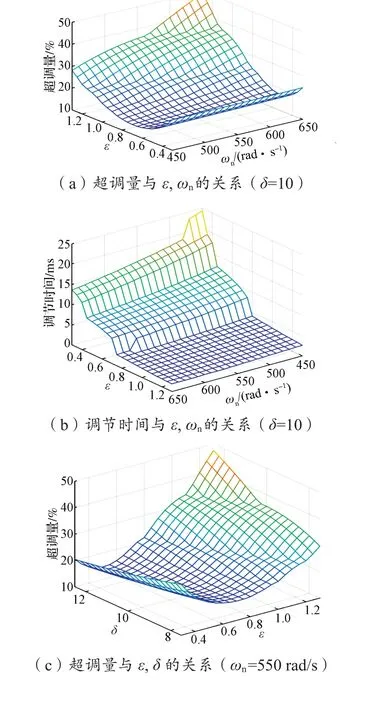
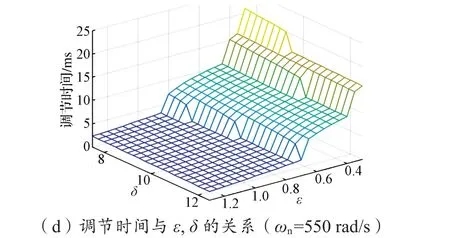
图6 阶跃响应下参数对超调量、调节时间的影响Fig. 6 In fl uence of parameters on overshoot and adjustment time under step response

2.3 动态响应仿真

综合考虑三阶角度跟踪观测器的系统带宽、超调量与调节时间后，选取如下控制参数：ωn=556 rad/s，ε=0.85，δ=10.7。由此得到三阶角度跟踪观测器90°阶跃响应、加速度(10 000 rad/s2)响应以及角度突变动态测试的仿真曲线（图7～图9）。图9示出角度突变时动态响应仿真波形：在0.5 s时刻，给定角度从180°突变到135°；约经过4 ms后，跟踪角度基本与给定角度重合，即动态响应时间为4 ms左右，可见三阶角度跟踪观测器可以很好地跟踪给定角度。

图7 90°阶跃响应仿真波形Fig. 7 Simulation response curve of the observer in the case of 90°step

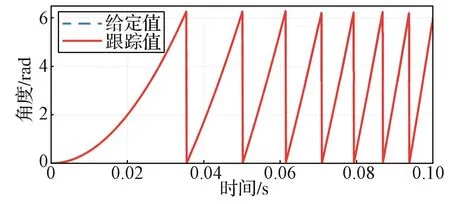
图8 加速度为10 000 rad/s2时响应仿真波形Fig. 8 Simulation response curve of the observer as acceleration is 10 000 rad/s2

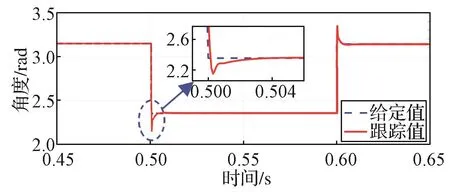
图9 角度突变动态响应仿真波形Fig. 9 Simulation dynamic response curve of the observer in the case of angle mutation

3 实验结果

为了验证三阶角度跟踪观测器旋变软件解码算法的正确性，设计了一种基于MPC5643的电驱动控制系统。其中旋变部分既保留了传统的硬件解码电路（AD2S1210），又增加了基于三阶角度跟踪观测器的软件解码电路，并在电机轴上安装了两个型号一样的旋变传感器（4对极）。受实验设备惯性的限制，现实的实验环境中很难模拟出几十度角度的阶跃，因此对旋变软件解码的验证分两阶段进行：第一阶段为单板测试，主要目的是测试三阶角度跟踪观测器的动态性能；第二阶段为系统台架测试，主要目的是测试旋变软件解码系统的整体性能指标。

3.1 单板实验

在单板测试阶段，采用程序编程模拟给定角度的方式对角度跟踪观测器算法进行验证。程序给定角度值和算法输出值被存储在预定的数据缓存区中，测试结束后通过CAN总线将数据发送到上位机进行分析。图10示出90°阶跃响应实验波形，其调节时间在4 ms左右，超调量20%左右，与仿真结果一致。图11示出角加速度为10 000 rad/s2时的响应实验波形，可以看出，角加速度跟踪误差在±0.001 rad/s2左右。图12示出角度突变测试实验波形，在25 ms时刻，角度从180°突变到90°，4 ms内跟踪上给定角度值，可见角度跟踪观测器的动态响应时间在4 ms左右，与仿真结果相一致。由图10～图12可以看出，单板测试波形与仿真波形基本一致。

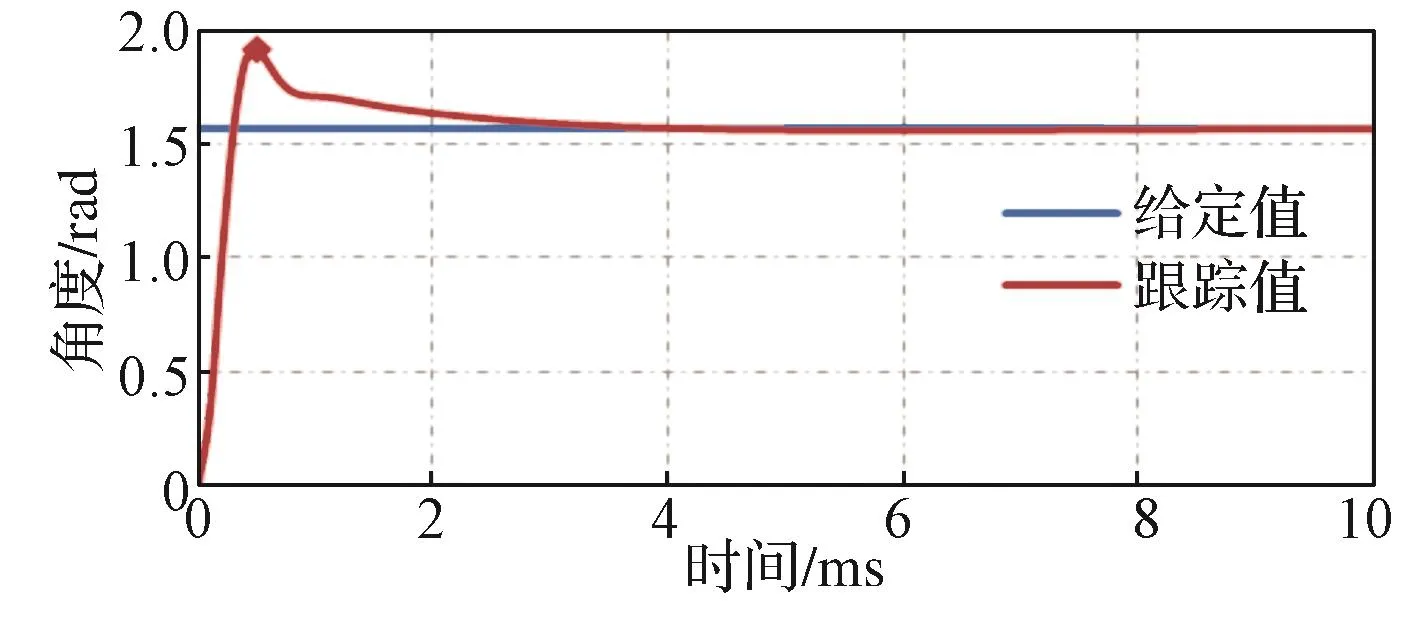
图10 90°阶跃响应实验波形Fig. 10 Experimental response curve of the observer in the case of 90°step

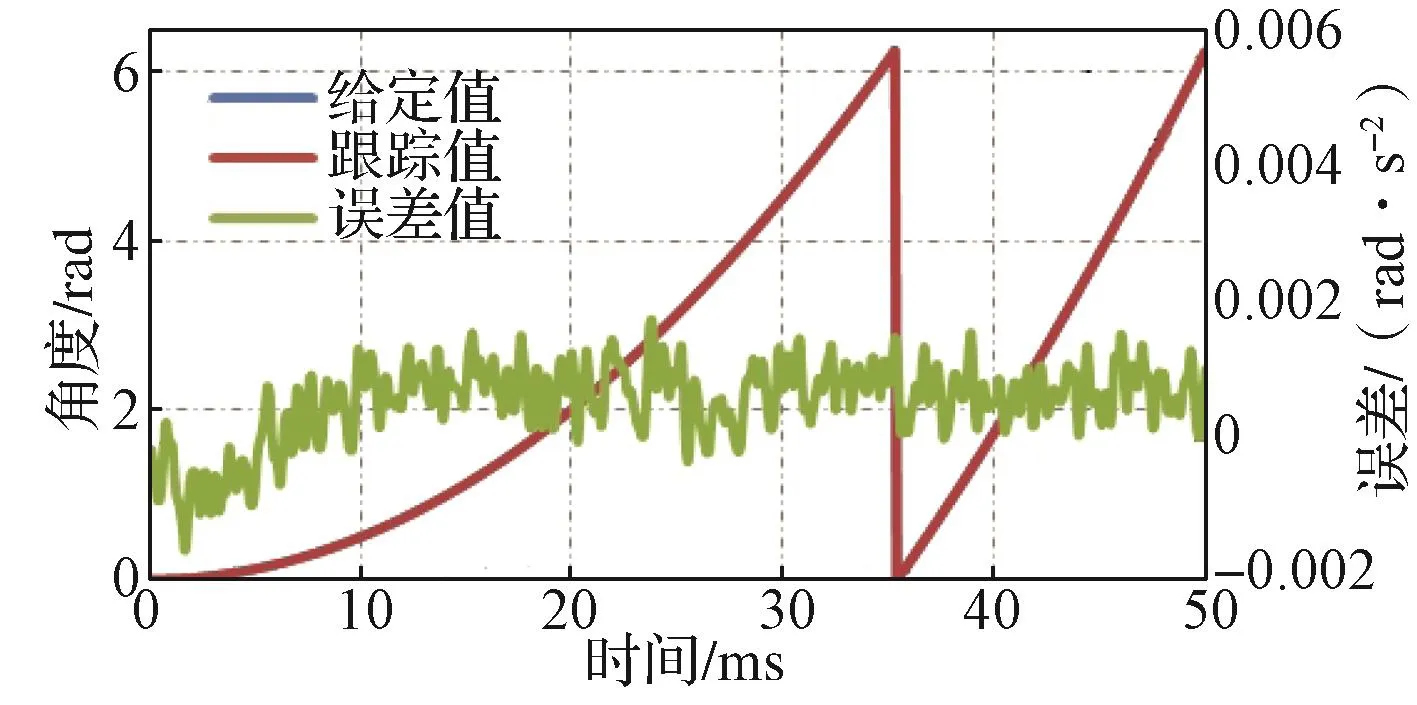
图11 加速度为10 000 rad/s2的响应实验波形Fig. 11 Experimental response curve of the observer as acceleration is 10 000 rad/s2

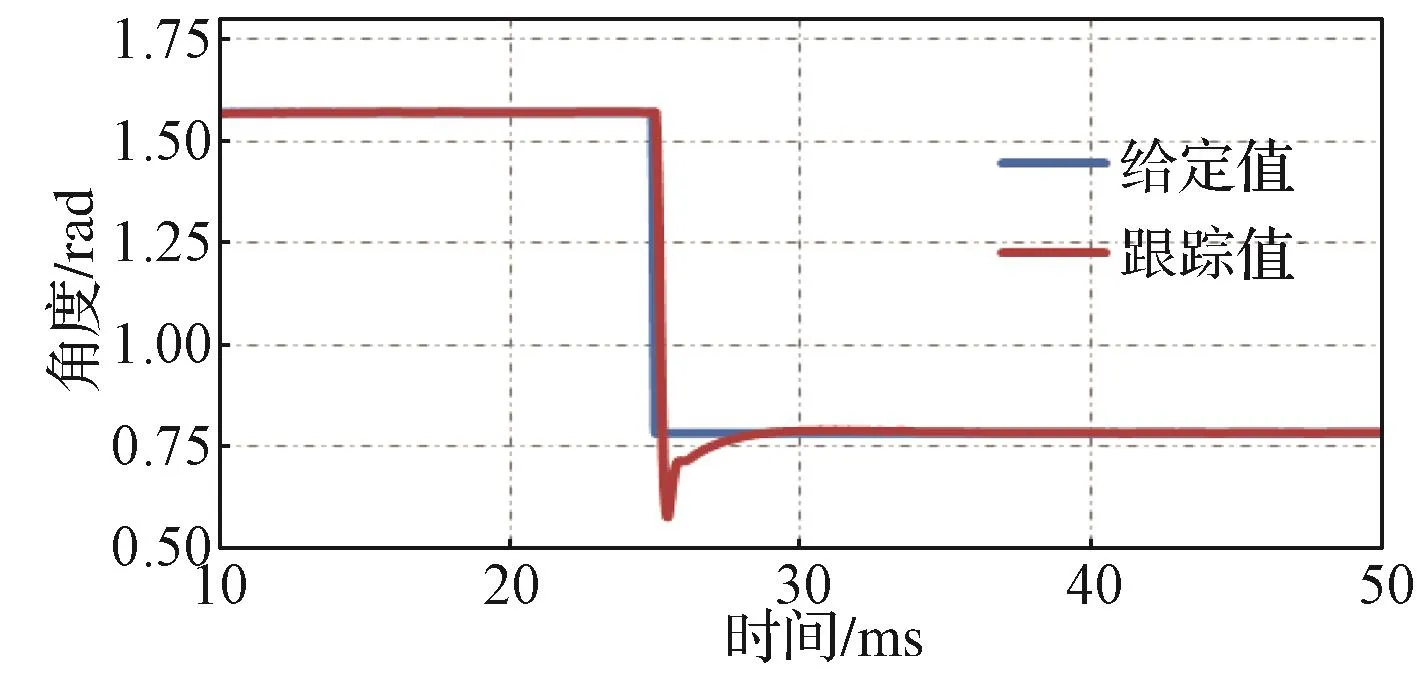
图12 角度突变测试实验波形Fig. 12 Experimental curves of the angle mutation dynamic response

3.2 系统台架测试

在系统测试阶段，对比测试了传统的旋变硬件解码与软件解码两种解码方式。实验台架测试平台如图13所示。测试过程中，通过上位机下发指令对硬件解码数据和软件解码数据进行存储，存储完毕后将数据发送给上位机进行分析。将测试数据整理后得到图14～图15的实验波形。从实验波形来看，软件解码输出角度与硬件解码输出角度间的误差基本在±1.0°内。该角度误差还包含了两个旋变机械位置的安装误差。两种解码方式下电机的外特性曲线高度一致，说明软件解码方式完全可以满足工程实际要求。

图13 台架测试平台Fig. 13 System test platform

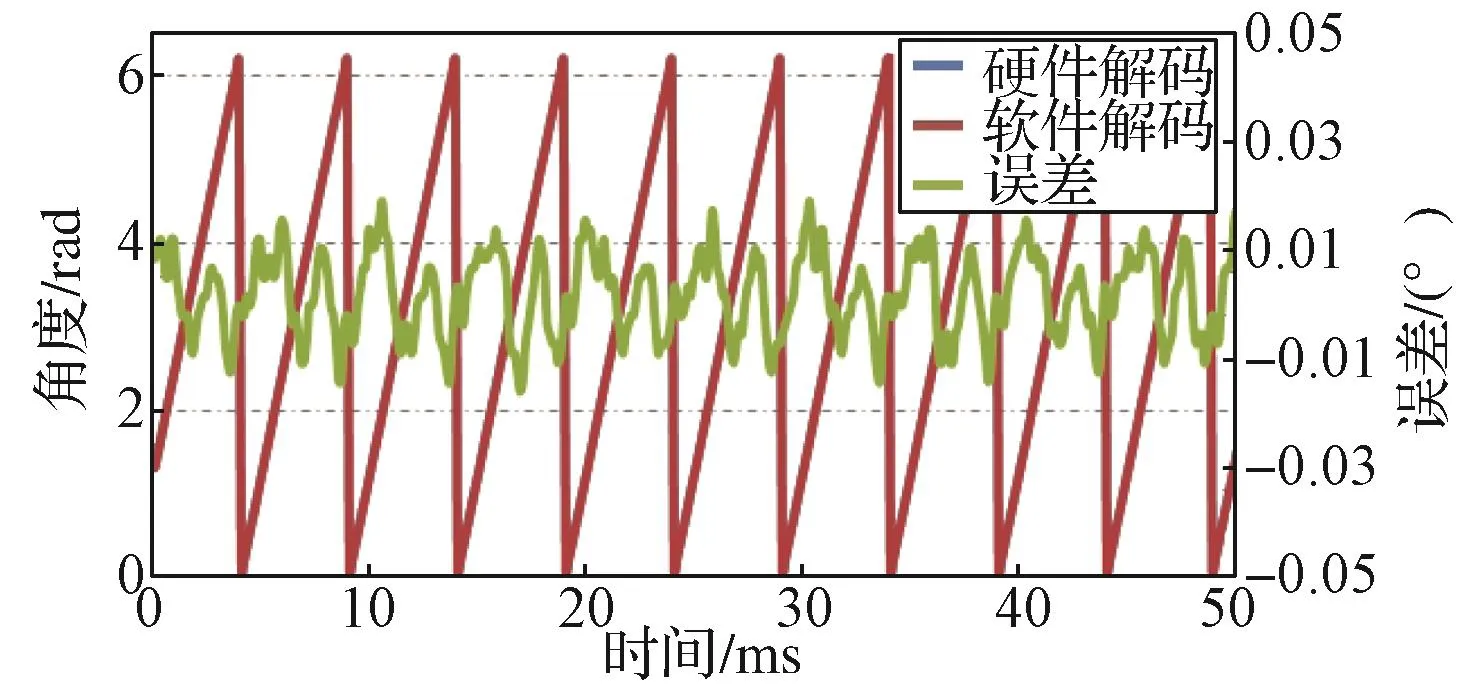
图14 转速3 000 r/min时的软件解码与硬件解码角度Fig. 14 Software-decoding angle and hardware-decoding angle of resolver as speed is 3 000 r/min

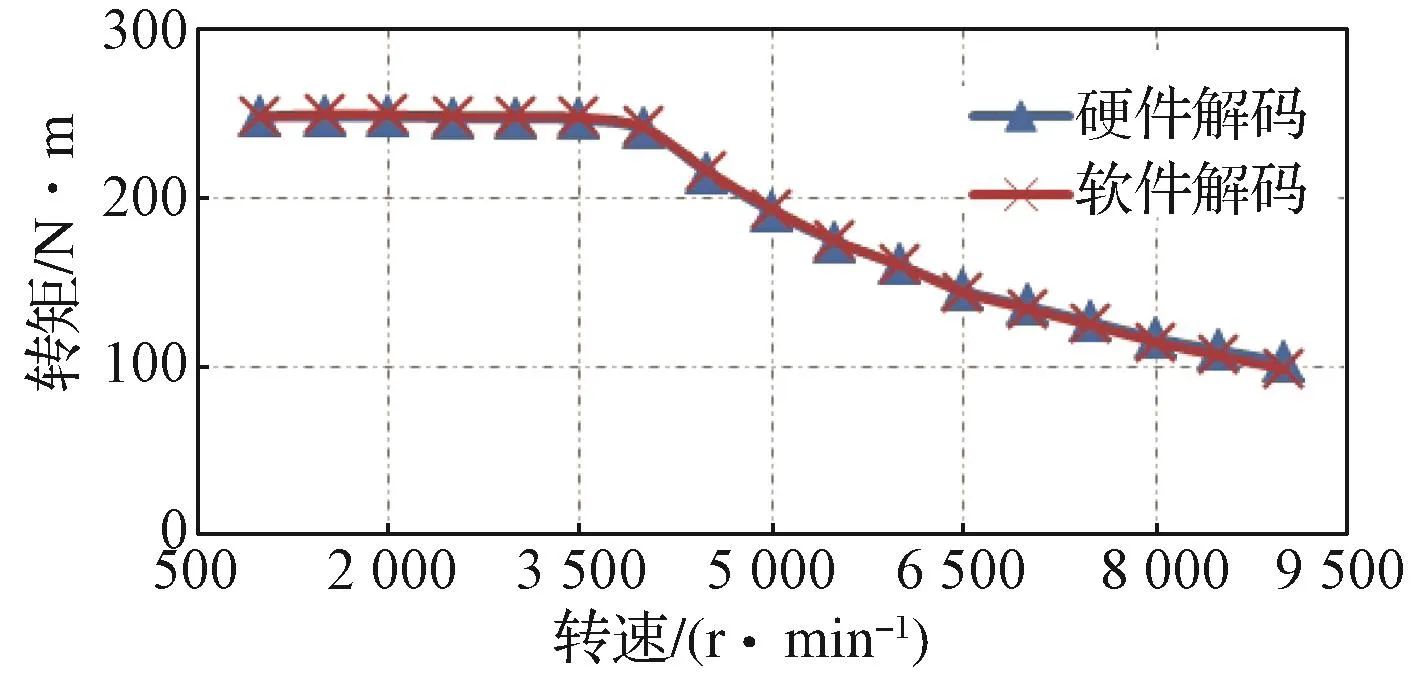
图15 软件解码与硬件解码下电机机械特性曲线Fig. 15 Mechanical characteristic curves with of motor softwaredecoding and hardware-decoding

4 结语

本文研究了基于三阶角度跟踪观测器的旋变软件解码算法，设计了基于该算法的旋变软件解码系统。仿真及实验测试结果表明，该解码系统具有较高的准确度，输出角度与硬件解码的相比偏差在±1.0°范围内，能够替代硬件专用解码芯片，从而节省系统成本，具有较高的工程应用价值。为了进一步提高旋变软件解码的性能，下一步将对故障诊断以及信号异常下的角度跟踪等方面进行研究。