积累活动经验 发展数学思维

文/中山市石岐高家基小学 黄建光

《全日制义务教育数学课程标准(实验稿)》在基本理念中明确指出，使学生“获得广泛的数学活动经验”。这是我国第一次将对经验的认知纳入了数学教学和数学学习之中。《数学课程标准(2011年版)》进一步将其纳入课程目标的“四基”之中，即“基础知识、基本技能、基本思想、基本活动经验”。这种递进式的变化，使我们认识到了“经验”对学生的学习，尤其对学生数学水平的提升和数学思维能力发展的重要性。作为小学数学一线教师，应注重学生基本活动经验的积累，让学生在活动中发展思维，增长智慧。

一、直观展示教具，唤起认知经验

【教学片段一】

1.请同学们回忆平方厘米、平方分米、平方米等面积单位的大小并汇报。学生一边汇报教师一边展示相应面积单位的正方形纸板。

2.学生回忆公顷与平方千米的大小。

3.进一步建立公顷、平方千米这两个土地面积单位与平方米之间的联系：1公顷=( )平方米；1平方千米=( )平方米。学生继续观察1平方米的正方形纸板，然后自由想象：1公顷有10000个这样的1平方米纸板这么大，1平方千米有1000000个这样的1平方米纸板这么大。

通过展示1平方米、1平方分米、1平方厘米的正方形纸板，让学生再一次理解面积的概念，感知它们的大小，进一步形成表象。如何让学生进一步感知公顷和平方千米的大小呢？关键是要与平方米建立联系，通过观察1平方米的正方形纸板，让学生对公顷和平方千米这两个面积单位建立更清晰的表象。

二、组织探究活动，动手解决问题

【教学片段二】

1.复习已学过的图形(长方形和正方形)的面积计算方法。

2.出示金钟水库平面图(如图1)，抛出问题：如何测量金钟水库的面积？(学生各抒己见)

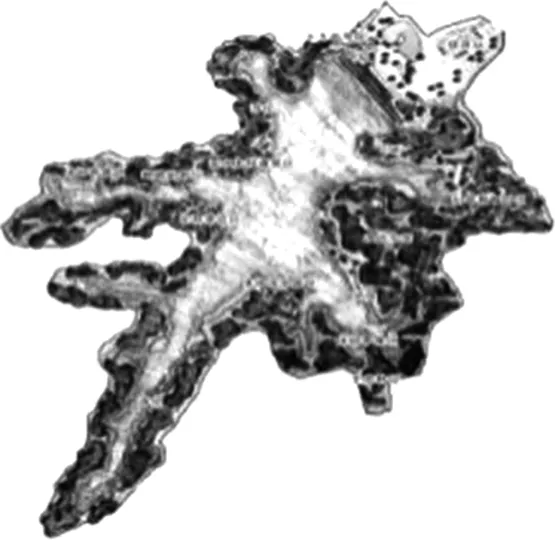
图1 金钟水库平面图

生1：参照求长方形和正方形面积公式的推导过程，把金钟水库的平面图切成一样大小的小块，数数有多少小块，再想办法求出每一小块的大小，就可以知道整个金钟水库的面积了。

生2：不可行，你看，金钟水库的边都是弯弯曲曲的，怎么可能切得一样大小的小块？

生3：可以把它切成一块块小正方形。虽然它的边弯弯曲曲，但我们可以把每一小块近似地看成正方形就可以了。

3.出示老师切割好的金钟水库平面图(如图2)，并提出问题：所有小正方形的面积之和，与金钟水库的面积相等吗？

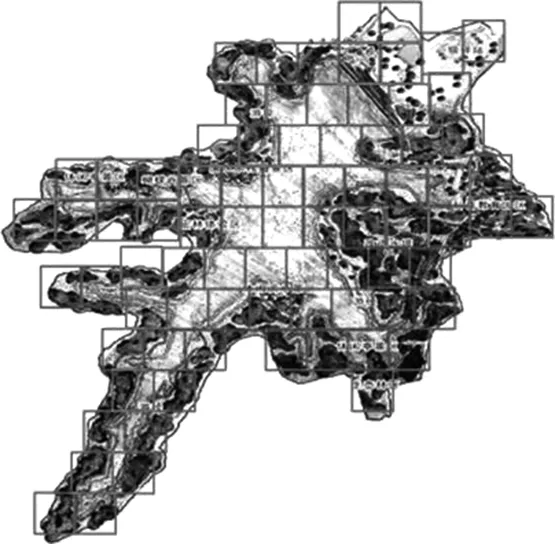
图2 切割好的金钟水库平面图

生1：不相等。你看，在平面图的周围，有些地方没有算进去。而有些地方不属于金钟水库的，却算到小正方形里面去了。

生2：但是与金钟水库的面积非常接近。少算了的面积与多算了的面积基本上差不多。所以所有小正方形的面积之和大约等于金钟水库的面积。

4.请同学数一数一共有多少块小正方形(学生的答案有78、80、81、82等)

5.有没有更简便的方法准确地计算出一共有多少个小正方形呢？

生：可以把他们的位置重新摆一摆，看看能不能摆成一个大的长方形或者正方形。这样就不用数得那么辛苦了。

6.学生分小组进行操作活动，并计算出一共有80个小正方形。

7.以拼成长10格，宽8格的长方形为例(如图3)，根据老师给出的数据计算面积。

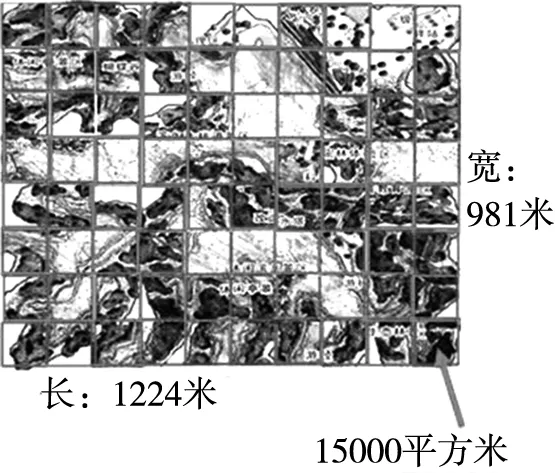
图3

1224×981≈1200000(平方米)

15000×80=1200000(平方米)

8.引导学生单位换算：1200000平方米=120公顷=1.2平方千米。

9.学生谈感受。

生1：金钟水库真的好大啊！

生2：我在金钟水库走一圈，都几乎累坏了。整个金钟水库才只有1平方千米多一点。这1平方千米该有多大呀！

生3：我现在大概能想象出1公顷和1平方千米有多大了。

生4：我现在大概知道1平方千米到底有多大了。就是差不多整个金钟水库这么大。

生5：原来不规则图形的面积还可以这样计算！

……

在复习环节，学生已经建立了公顷与平方米、平方千米与平方米之间的联系。但是这两个单位对于学生来说依然很抽象。本环节，通过一系列的活动，让学生了解金钟水库的面积，知道金钟水库的面积是120公顷或者1.2平方千米，最后通过与金钟水库的对比，进一步感知1公顷和1平方千米的大小。另外，学生三年级学习长方形和正方形的面积时，就是通过切割的方法得到长方形和正方形面积计算公式的。因此，有一部分学生很容易就想到利用切割的方法来求金钟水库的面积。同时，教材在五年级安排了平行四边形、三角形和梯形的面积、估计不规则图形的面积，在六年级安排了圆的面积，这些图形的面积计算方法都需要利用转化思想或估算的方法。本环节把不规则的金钟水库平面图转化成长方形或者正方形，对转化的思想起到渗透的作用，为日后自主学习多边形的面积计算打下坚实的基础。

本节课授课前，教师先让家长周末带学生到金钟水库游玩，让学生在户外活动中充分感知金钟水库的大小。在课堂教学中，教师通过设置有趣的课堂活动，给予学生足够的时间和空间探索如何测量金钟水库的面积，通过动手拼一拼、算一算和汇报等活动，一步步地引导学生如何测量金钟水库的面积，让学生进一步积累“把一个图形转化成已学图形来求面积”的经验，发展学生的数学思维，感受转化数学思想的应用。

“儿童的智慧在他的手指尖上。”只有学生不断地积累丰富的数学活动经验，在活动中不断展现学生思维的过程，学生才能在以后的学习中更积极主动地思考，探索新知识才能更加得心应手。