高中教师资格考试高等代数试题分析与教学思考

程晓亮，付 泽，郑 晨

目前，除内蒙古、新疆、西藏等少数几个省市的师范生外，其他省市的师范生和非师范生均需通过全国统一的教师资格考试这一必要条件，才能获得教师资格证书，从事教师职业.全国教师资格统考由笔试和面试两部分组成，普通高中数学教师笔试考三个科目，即综合素质、教育知识与能力和数学学科知识与教学能力，三科均合格才可以参加面试.就笔者所在单位参加考试和所了解的情况看，三个科目中数学学科知识与教学能力通过率相对较低.这一科目笔试包含数学学科知识、课程知识与教学知识等方面，而数学学科知识不仅涉及数学专业基础课中的数学分析、高等代数、解析几何、概率论与数理统计等内容，也涉及其他课程的基础内容与思想方法.现对2014 年—2019 年全国教师资格考试数学学科知识与教学能力科目中出现的高等代数题目加以统计分析，以期在课程建设与教学改革方面得到一些启示.

1 高等代数题目的统计分析

1.1 数学学科知识与教学能力试卷整体情况

全国教师资格考试数学学科知识与教学能力科目的考试时间为120 分钟，满分150分，考试形式为闭卷.试卷由选择题、简答题、解答题、论述题、案例分析题、教学设计题六种题型组成，其题目数与分值情况大致如下：选择题8 道，每小题5 分，共40 分；简答题5道，每小题 7 分，共 35 分；解答题 1 道，共 10分；论述题 1 道，共 15 分；案例分析题 1 道，共20 分；教学设计题 1 道，共 30 分 .整张试卷中，论述题、案例分析题、教学设计题考查课程知识与教学知识，选择题和简答题中也有部分内容涉及课程知识与教学知识；考查数学学科知识的题型主要是选择题、简答题和解答题，题目分数占比约为40%.

1.2 试卷中高等代数内容统计分析

2014 年—2019 年全国教师资格考试数学学科知识与教学能力科目，共计11 套试卷，其中有28 道题目考查了高等代数内容.高等代数课程的知识点总体可以分为：多项式、行列式、线性方程组、矩阵、二次型、线性空间、线性变换、欧氏空间等［1-3］.在 11 套试卷中，矩阵考查次数最多，共考查7 次；其次是对线性方程组的考查，共考查6 次；对线性变换共考查5 次；对多项式、线性空间、二次型、欧几里得空间以及行列式的考查为1～3 次.除此以外，通过对11 套试卷的统计可知，在教师资格考试中高等代数考查的试题类型为以下三种：单项选择题、简答题和解答题.具体如图1 所示.

图1 11 套试卷中题型与题目数统计

从图1 可以看出，多项式仅以选择题的形式考查2 次；行列式仅以选择题的形式考查1次；线性方程组考查形式分别为选择题和简答题，各考查3 次；矩阵以选择题的形式考查3 次，以简答题的形式考查4 次；二次型仅以选择题的形式考查2 次；线性变换以选择题的形式考查5 次；线性空间的考查形式为选择题、简答题和解答题，各考查1 次，而且这是11 套试卷中唯一一道以解答题形式考查的知识点；最后是欧几里得空间分别以选择题和简答题的形式各考查1 次.由此可见选择题和简答题是历年的必考题型，其中选择题考查学生的基础知识和运算能力；简答题考查学生的分析问题和解决问题的能力；虽然在11套试卷中，解答题仅考查一次，但考查的是学生综合运用的能力.

11 套试卷中所考查的各知识点的分值情况统计如图2 所示.

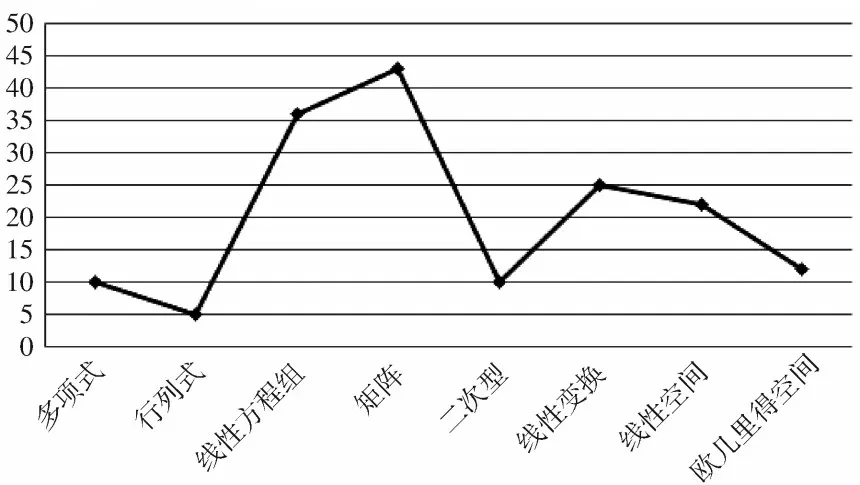
图2 各知识点与分值情况统计

从图2 可以看出，矩阵考查的分值最高；其次是线性方程组；排在第三位的是线性变换.

高等代数内容总体知识点又可以分为各个具体知识点，其知识点类型分为定义、公式与法则、定理及其应用.11 套试卷考查定义12次、考查公式与法则6 次、考查定理及其应用7 次.可见教师资格考试不仅考查学生对基础定义和重要概念的理解、考查学生对高等代数中重要的公式法则和定理的掌握、更重要的是考查学生对数学思想方法的掌握和综合运用的能力.

2 试卷中高等代数典型问题解题分析

2.1 概念性问题解题分析

2018 年上半年高中数学教师资格考试，数学知识与教学能力科目中简答题第9 题为高等代数问题，考查在什么条件下，一个二阶矩阵存在逆矩阵，并求出其逆矩阵.

该题目考查的是矩阵可逆的定义以及求矩阵的逆矩阵的方法，即求逆矩阵的公式.解题的关键首先是掌握逆矩阵的定义及其等价条件.方阵可逆等价于其行列式不为零，等价于其行向量（列向量）组线性相关，等价于其特征值均不为零，等等.由此可见，这里蕴含着高等代数中的诸多关键性概念.另外，当一个矩阵可逆时，求其逆矩阵的方法也不唯一，这里由逆矩阵与伴随矩阵之间的关系，很容易求出逆矩阵.只从能够解题的角度来看，该问题就是考查了矩阵可逆的定义、二阶行列式的定义、伴随矩阵的定义及利用其求逆矩阵的公式，属于着重考查概念的问题.具体解答程序：利用行列式不为零得出矩阵存在逆的条件，再利用伴随矩阵的定义求出伴随矩阵，最后由逆矩阵与伴随矩阵之间的关系求出逆矩阵.

2.2 定理性问题解题分析

2016 年下半年高中数学教师资格考试，数学学科知识与教学能力科目中简答题第10题：叙述一般的非齐次线性方程组有解的充要条件；并求一个含有四个未知元，三个方程的非齐次线性方程组的通解.

一般的线性方程组有解的充要条件是系数矩阵的秩与其增广矩阵的秩相同，当然，据此齐次线性方程组必然有解，并且有无穷多组解.为了求出一般非齐次线性方程组的通解，只需要找出该线性方程组的一个特殊解以及导出组的全部解，进而需要求出对应的齐次线性方程组的基础解系，以此表示出其所有解.这里考查的是线性方程组有解的判定定理、非齐次线性方程组与其导出组的解之间的关系定理以及解线性方程组的方法.属于考查基本定理以及求解公式范畴.具体解题程序：首先对非齐次线性方程组的增广矩阵进行初等行变换，得出与其同解的简化方程，求出一个特解；再求出对应的齐次方程组的基础解系；最后表示出原方程组的通解.

基于对国家教师资格考试中高等代数内容的统计与分析，为切实提高课程的教学质量，对高等代数课程的教学需要进行一些反思.

3 高等代数课程的教学思考

高等代数是所有数学教育专业都需要开设的一门基础课，一般在大学的第一、第二两个学期开课，每周 4 学时左右［4-5］.作为第一学期开设的课程，学生一般需要转换学习的方式方法，来适应课程的学习.根据国家教师资格考试中针对高等代数课程的内容及特点，在教学中需要关注以下两个问题.

3.1 联系初等数学深化基础知识的教学

《普通高中数学课程标准（2017 版）》中明确指出，数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是数学学习和应用的过程中逐步形成和发展的［6］.高等代数所体现的核心素养包括：数学抽象、逻辑推理、数学运算、数据分析.核心素养这一概念对数学教育提出了更高的要求，课程改革需要不断地应对时代的挑战.高等代数是初等数学中代数知识的推广和一般化，是在具体的代数结构的基础上得出的公理化的论述，也就是从个性中提炼出来的共性.在课程教学改革实践中，不仅要挖掘初高等代数知识体系方面的联系，更要挖掘数学思想方法、数学观念方面的联系［7］.绘制知识结构框图与思维导图，展示初高等代数知识和思想方法的整体结构、体现新旧知识之间的联系、凸显数学学科核心素养.在此基础上，使学生更加深刻的理解新知识的本质和规律.

高等代数是中学数学的深入和提升，它不仅解释了许多中学数学中没能解释清楚的问题.例如，线性方程组理论、多项式的根及因式分解理论等，而且还以中学数学中所涉及的平面向量、实数为例，引入了向量空间、数环、数域，进而引入了欧氏空间等代数系统.因此，教学中可以充分考虑中学数学所学，循序渐进的引导学生认识知识与思想方法的一般化过程，进而再利用高等代数的观点和方法来指导学生的中学数学的学习.中学代数讲过简单线性方程组的解法，高等代数中讨论一般线性方程组有解的判断及其解法，可以利用初等代数的具体例子详细演示一般化过程，降低新知识学习的难度.同时，在学习了一般有限维欧氏空间等高等代数知识后，再去考虑中学数学中二维平面和三维空间的向量及其各种运算、坐标系与坐标轴、长度以及各种角度问题时，便非常清晰明了.引导学生将大学知识与中学知识串联起来，站在更高的层次去看待中学的知识，顺利实现思维方式和学习方法的过渡与转变.利用高等代数的理论、方法和观点去剖析中学数学的方法和问题，深刻理解中学数学有关知识内容的来龙去脉.

3.2 结合知识体系的构建加强解题训练

数学学科具有高度的抽象性，严密的逻辑性.数学学科知识与教学能力科目中的高等代数试题在充分体现学科特点的前提下，将高等代数知识进行整合，结合教材选取有代表性的母题进行演变，全面考查高等代数基本的定义、性质、定理及应用，强调各知识之间的内在联系，充分的检测学生的计算能力、逻辑推理能力、综合分析能力等数学能力，而不是孤立的考查某一种能力［8］.同时还涉及到对高等代数的思想方法的考查，高等代数的数学思想包括：抽象性思想、公理化思想、一般化思想、初等变换的思想、辩证思维的思想、关系映射反演思想等.教学中不仅要注重让学生理解概念的背景，定理的推理过程及应用，更应该使其掌握高等代数的思想方法以及某些现实来源；不仅要重计算，更要重理论；不仅要重解题，更要重应用.在遵循数学学科特性的基础上，通过不断地分析、综合、运算、判断、推理，将数学学科核心素养与高等代数的教学有机融合，指引着教育模式和学习方式的根本性转变［9］.只有综合而全面地学习和理解才能真正的培养学生的抽象思维，提高逻辑推理能力，养成应用意识，提升数学素养.

通过前面的分析可以知道，矩阵、线性方程组和线性变换这三个知识点无论是在题目数量、题型还是分值统计等方面考查的居多，如果对高等代数的知识体系比较了解，就可以理解这些题目出现的必然性.因此在加强解题实践的过程中，应该侧重引导学生构建高等代数知识体系，深化对高等代数课程的认识，从而进一步提升解决问题的能力，形成良性循环.

4 结语

数学学科知识与教学能力科目中数学学科知识这部分，往往通过考查学生应用知识的能力，来考查学生的学科知识素养.其中，高等代数的内容相对抽象，与其他科目特别是解析几何交叉融合.通过国家教师资格统一考试是从事教师职业的“敲门砖”，同时，考试的通过率也反观了高等师范院校的教育教学质量.高等代数是数学专业一门重要的基础课程，任课教师应该关注国家教师资格考试中高等代数所考查的内容，以此作为一个切入点，思考如何进行教学改革，才能提高教学效果，促进学生长远发展.