基于数据拟合方法的电池剩余放电时间模型研究

高继文

自普兰特1859 年发明铅酸蓄电池以来，其广泛用于军事、日常生活等各个方面.铅酸电池放电过程中，在持续不变的电流强度下，电池的电压变化呈现出一定的规律性，电压随着放电时间的增加而不断下降，直到降至一个固定数值，称之为最低额定保护电压，记为Um，且Um=9.0 V.当电池被充满电后，开始让它放电，随着时间变化电压也会相应变化的趋势关系称之为该电池的放电曲线.文章将电池在现阶段能够持续供电的时间以及放电到保护电压所需的时间作为探讨的主要对象，其中提供的相关电池数据来源于相同批次，当其出厂时以不同的电流进行相关放电测试研究，相同的电池在不同的衰减状态下，再以相同的电流从充满电状态起，对其放电进行相关记录.并需要解决以下问题：

其一，已给出相同的生产批次电池放电测试情况，请根据相关信息建立其放电曲线，再利用建立的放电曲线数学模型，当电压为9.8 V 时，分别以30.0 A，40.0 A，50.0 A，60.0 A和70.0 A 不同的电流强度放电，求其相应的剩余放电时间是多少.

其二，试以20.0～100.0 A 任意一个恒定的电流强度下，构建相应的放电曲线数学模型，同时利用MRE 值对模型的精度进行评估.当电流强度I=55.0 A 时，绘制其放电曲线图.

其三，同一个铅酸电池在不同衰减状态下，以相同的电流强度从充满电开始，观察记录其放电状态，在已提供的衰减状态3 下，试着讨论预测电池的剩余放电时间（文中提到的3 个衰减状态及相关数据均来自于2016 年全国大学生数学建模竞赛C 题及附件数据）.

1 模型的建立

因为机器所需的电源如果发生故障，需要有后备的电池提供电源供给，但是如果在实际工作中没有预先发现备用蓄电池问题，这些疏忽都将导致无法挽回的损失.因此，检测蓄电池健康运行状态是整个行业的重点研究方面之一［1］.

1.1 放电曲线的多项式模型

利用已有数据，提取电流强度与放电时间的相关数据，列出9 个电流强度值与分别对应的放电时间关系表，如表1 所示.

表1 电流强度与放电时间变化表

显然，基于表1 的数据变化，可得出电流强度与放电时间的一一对应关系，绘制出散点图，如图1 所示，从而可直观地看到放电时间的变化情况.

根据对应关系，容易得出结论：随着电流强度逐渐增大，放电时间逐渐减小.通过已给数据，同一个批次的电池出厂时，用不同的电流强度进行放电测试，考虑到起始阶段电池电压稳定性不够，所以对30 min 后的电压情况进行研究更具有代表性.综合比较后利用三次函数模型进行拟合，利用EXCEL 画出相应的放电曲线图，如图2 所示.

图1 电流强度与放电时间变化图

图2 电池电压与时间变化的放电曲线

从图2 可以看出，不同的电流强度下，电池电压会逐渐降低，不断接近额定的最低保护电压，同时放电时间也不断增加.通过拟合的方法，容易得出电池电压U关于放电时间t的多项式数学模型，模型如下：

其中：ai(i=0,1,2,3)为相关系数.

结合图2，在不同的电流强度下，对电池电压与时间进行拟合，可以得出9 个三次函数多项式回归方程，在此不一一列出.

1.2 MRE（平均相对误差）模型

由MRE定义，建立如下模型：

根据平均相对误差的定义，可知放电曲线在低压段的质量决定了电池放电时间的精度.考虑到电池放电曲线的采样，在相同时间间隔下，电压不高阶段的样本点相对较稀.所以已有数据中从Um开始最大间隔小于等于0.005 V，从中总计提取电压的样本点个数为231 个［2］.

根据公式（1）可得，当I=80.0 A，构建时间T与电压u的三次函数多项式模型，即：

其中：ki(i=0,1,2,3)为相关系数，u为电压.

当I=80.0 A 时，所对应的三次函数为：

从数据中可以看出，Um开始按不大于0.005 V 的最大间隔，一共提取231 个电压的样本点，即设N=231，当I=80.0 A 时，MRE=0.006 51.按照相同的计算方法，不同的电流强度所对应的MRE值，如表2 所示.

表2 不同电流强度对应的MRE 值

1.3 电池剩余放电时间模型

由模型（3）易知，时间T与电压u的三次多项式模型，即T(u)=k3u3+k2u2+k1u+k0，（其中ki，i= 1，2，3 为相关系数），恒定电压下，在以不同电流强度通电状态下，可以求解相应的剩余放电时间，求解模型如下：

在电压恒定下，即电压u=9.8 V，以I=70.0 A 时为例，则可得出T(u)=-70.391u3+1 621.8u2-12 132u+29 999，R2=0.999 9.

对该方程分别以电压u=9.0 V 和u=9.8 V代入求解，最后可求得TS=250 min.同理在其他的电流强度下，所对应的剩余放电时间也可一一求解，具体如表3 所示.

表3 不同电流强度下电池的放电时间

2 模型的求解

分析9 个不同电流强度下三次函数多项式的参数，同时观察电流和多项式模型参数值的相关变化，利用MATLAB 软件进行分析，当电流数值提高十个数量级时，所对应的参数值也降低一个数量级，而单调性始终不变.因此，指数函数模型的特性比较适合［3］，检验后，发现拟合的效果较好，故建立优化的数学模型，模型如下：

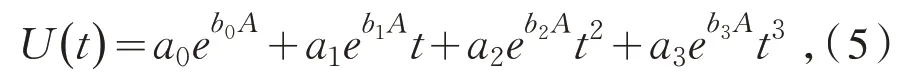
其中：ai,bi为参数，i=0,1,2,3，A,t为自变量.

利用MATLAB 软件，将EXCEL 的数据导入后，可得式（5）的参数值如表4 所示.

接着对已求解得到的数学模型，借助MATLAB 软件画图、拟合等功能，逐步编程后拟合出电流强度为55 A 的放电曲线［4］，放电曲线如图3 所示.

表4 参数值列表

图3 电流强度为55 A 时的放电曲线

利用已建立的数学模型，通过编程便可得到不同电流强度所对应的MRE值，如表5所示.

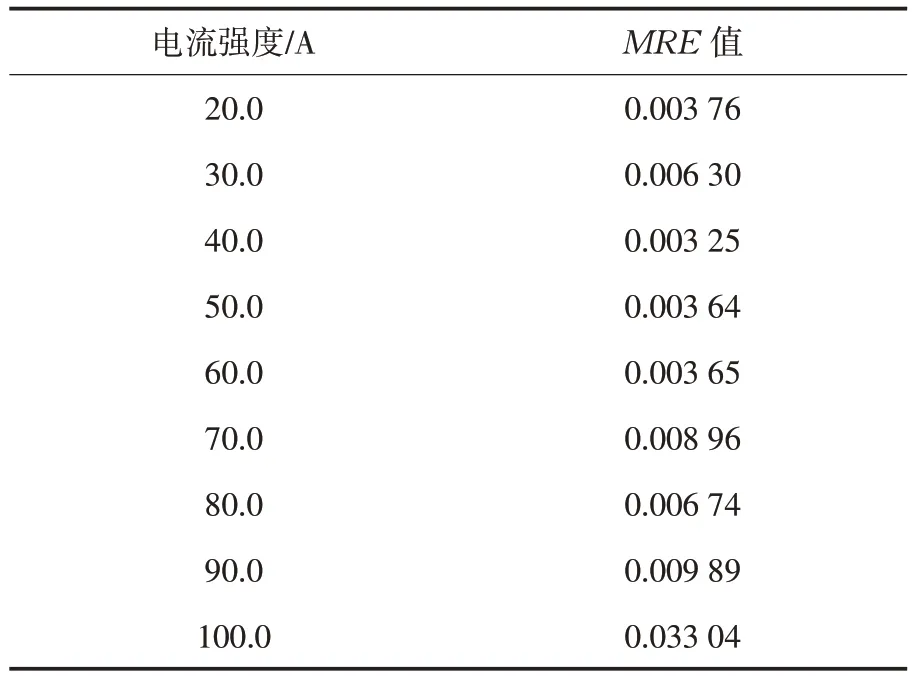
表5 不同电流强度对应的MRE 值

先对数据中衰减状态3 的剩余放电时间进行初步分析，再利用MATLAB 软件中cftool分析工具的帮助对得出的数据进行拟合分析，容易得出所建立的函数是单调递减的，同时可以用3 次函数模型来拟合［5］，所以可得模型如下：

利用MATLAB 软件，将已得到的EXCEL数据导入后，对需要求解的参数通过软件语言进行编程.由于电池在放电过程中，其电压在起始阶段稳定性差，因此对30 min 后的放电曲线状态进行考查研究［6］，利用相同的方法进行数据拟合，采用三次函数模型建模，并较容易的利用MATLAB 画出电池放电曲线图，如图4 所示.

图4 30 min 后电池的放电曲线

利用EXCEL、MATLAB 对相关数据进行数据处理，得到相关函数模型为：

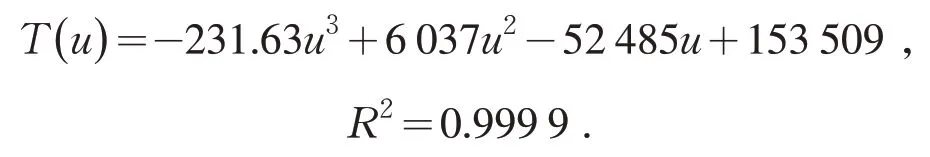
所以，当u=9 V 时，电池的剩余放电时间约为1 282.7 min.从而，得知这样的结果与新电池放电样本状态下的时间1 281.1 min 契合度较高［7］.遵循同样的步骤与方法可以很快确定在衰减状态1 和衰减状态2 下，当u=9 V 时的电池的剩余放电时间.

因为模型的误差分析情况是衡量所建立的数学模型精度必须完成的关键环节［8-9］.用已给数据，对电池状态中前3 个数据进行评估，然后利用预测得到的相关数据与实际的数据进行对比，将回归方程的误差和残差求出，残差的求解公式如式（7）所示.

通过计算，可得到三个状态下残差及预测值，具体如表6 所示.

表6 预测值及残差

利用表6 给出的数据，可以计算出残差绝对值与实际数据的比值.求解模型如下：

其中：Ct为残差绝对值和实际值的比值，|et|为残差的绝对值，St为衰减状态下的实际值.通过计算得到各状态下的相关比值，如表7 所示.

表7 不同状态下的比值

从表7 可以看出，每个状态下的比值都小于1%，所以拟合的吻合程度较高［10］.因此可以对衰减状态3 的剩余放电时间进行比较准确的预测.由于在30 min 前电池的稳定性较差，可以再次利用EXCEL、MATLAB 软件对数据进行处理，得到离散点，进而拟合出放电曲线如图5 所示.

图5 30 min 后衰减状态3 的放电曲线

根据图5 拟合得到曲线方程

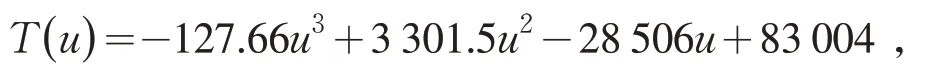
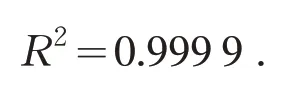
因此，当u=9.0 V 的电池在放电时间T=807.4 min 时，经计算可求出，在衰减状态3下，铅酸电池的剩余放电时间约为211 min.

3 结语

通过对已有数据进行适当地处理，建立了数学模型，并且绘制出相应的可视化分析图表，同时也对铅酸电池放电预测进行了深入探讨，在解决问题的思路和模型推广应用上可为其他同类问题的研究提供一定的借鉴.