永磁同步风力发电机系统的仿真与分析

张 宝，丁 文，冯翠彪，冯雪晨

现今，人类生活中电能需求越来越大，传统火力发电［1］所需的燃料大多属于不可再生能源，同时会产生有害气体.因此，研发可持续、更清洁的电能具有现实意义.

风力发电是现今普遍接受的发电技术，是将风中蕴藏的动能转换成电能的发电方式［2］. 在 风 力 发 电 技 术 中 ，永 磁 同 步 电 机（PMSM）扮演重要角色，具有效率高、功率因数高、维护成本低等优势，并且发电机技术已经相当成熟［3］.现代控制理论如神经网络控制、混沌控制、模糊控制等［4-6］，广泛应用于永磁同步电机控制系统中，取得了较好的效果.但在风力发电系统中，由于风速的复杂性，以及风力机的动态特性，使得上述控制方法得到的风能效率不高.滑模变结构控制能够有效地控制非线性系统，抗干扰能力强，能够自寻最优控制，适用于复杂的非线性风力发电系统.因此，本文以复杂的综合风为研究基础，建立永磁同步发电机数学模型，设计了PMSM 的滑模控制器，实现了风力发电机快速响应、稳定运行的性能.

1 风力机组数学模型

1.1 风速模型

风力发电系统是以空气动力学为基础的发电系统，风是整个系统的能量来源.风速不会长时间保持在一个恒定值，具有不确定性和随机性，导致风力发电系统所输出的功率也随着风速的变化发生变化，根据四分量法将风速分为基本风、阵风、渐变风和随机风［7-8］.则风速模型可表示为：

①基本风模型.该类风速表示一段时间内的平均风速，一般服从威布尔参数分布［9］，由此可以近似地确定其公式为：

其中：k和B分别是威布尔分布中的形状参数和尺寸参数［10］，这两个参数可以根据风电场的实测数据得出.

②阵风模型.该类风速表示风速突然变化时的状况，可用于探究在较大风速影响下系统的特性，得出阵风风速随时间变化的结论.

阵风模型公式如下：

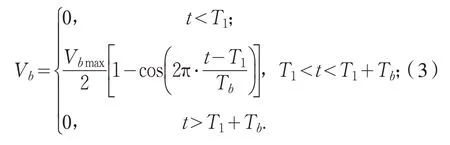
其中：T1为阵风起始时间点；Tb为阵风的周期；t为时间；Vb为阵风风速；Vbmax为阵风风速的峰值.

③渐变风模型.该类风速表示线性变化的风速，则可得出渐变风随时间变化.

渐变风模型公式如下：

其中：Tc1是渐变风起始的时间点；Tc2是渐变风结束的时间点；T是渐变风达到峰值后恒定不变持续的值；Vc是渐变风的风速值；Vcmax是渐变风风速的峰值.

④随机风模型.该类风速表示在一定的高度下风速随机变化的状况，其公式如下：

其中：Vd表示随机风的风速值；Vdmax表示随机风风速的峰值；ωi表示风速随机波动时的角速度；φi表示初相位；Random表示在-1 到1范围内均匀分布的随机变量.

1.2 风力机模型

风力机是利用风中蕴含的能量转化成机械能的一种装置.风吹向叶轮时，叶轮旋转将风能转化为作用于同步发电机转子上的机械能，同时将叶片转矩转化为同步发电机转子上的机械转矩［8］，则风力机所获得的机械功率可表示为：

风力机所获得的机械转矩可表示为：

其中：P为风力机所获得的机械功率；ω为风轮角速度；ρ表示空气密度；R表示风力机的半径；V表示风速；Cp(λ,β) 表示风能利用功率系数.

Cp(λ,β)表达式如下：

其中：λ表示叶尖速比；β表示浆叶节距角；Cf表示叶片的规定设计常数.

1.3 传动系统模型

本设计采用由低速轴、增速箱以及高速轴等组成的传动系统，将风力机所传输的机械功率经过增速后再作用于高速轴上，使发电机侧转子有足够的能量促使发电机发电.传动系统的结构如图1 所示.

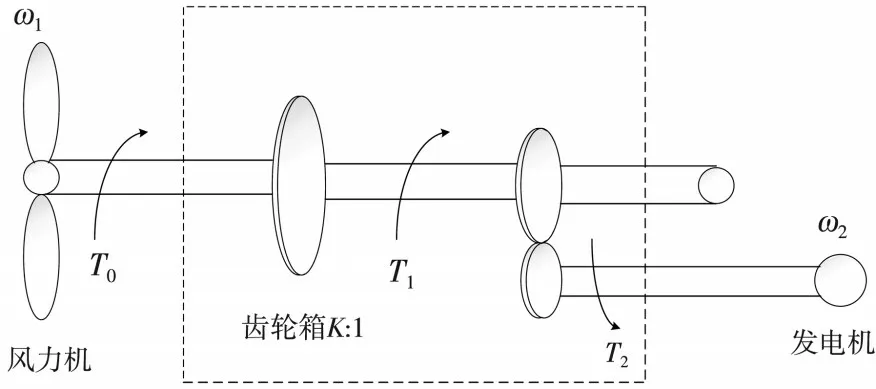
图1 传动系统结构图

风力机和发电机转轴的阻尼系数忽略不计［11］，则风力机侧的运动方程为：

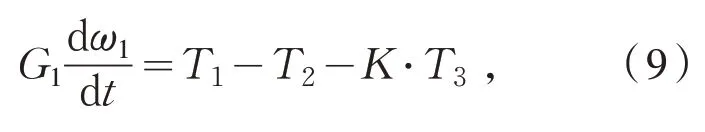
其中：G1表示风力机的转动惯量；ω1表示风力机侧风轮的角速度；T1表示风力机侧的输入机械转矩；T2表示风力机经低速轴传输至齿轮箱所需要消耗的阻力转矩；K表示齿轮箱的传动比例；T3表示经过齿轮箱到达高速轴的机械转矩.

发电机侧的运动方程如下：

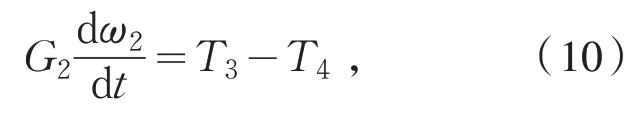
其中：G2表示发电机侧的转动惯量；ω2表示发电机转子的角速度；T4表示发电机内部的阻力转矩.

综合风力机侧和发电机侧的运动方程，得到质量块的公式为：

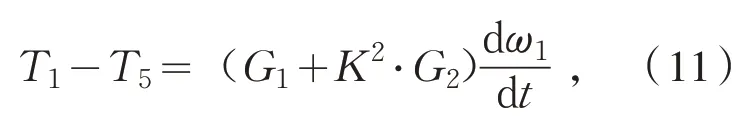
其中：T5表示低速轴上的机械转矩，且T5=KT3.

2 永磁同步发电机数学模型

为简化分析，假设定子绕组正弦分布，并忽略铁损、铁心涡流、磁路不饱和的影响，建立在d-q同步旋转坐标轴下的方程为：

式中：ud、uq为d轴和q轴的定子电压，id、iq为d轴和q轴的定子电流，Ψf为磁链，RS为定子电阻；Ld、Lq分别为d轴和q轴的电感.发电机的电磁转矩微分方程表示为：

由于风力发电的PMSM 多用径向表面式分布，有Ld=Lq，因此式（13）可写成：

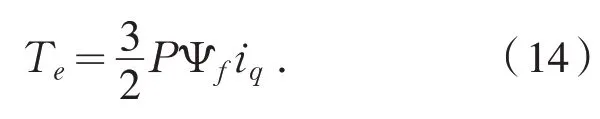
机械运动方程为：

式中：TL为负载转矩；J为风力机与发电机连接轴间的等效转动惯量.

3 滑模变结构控制器的设计

在控制系统中，滑模变结构控制能够实现非线性控制.通过构造超平面使其沿着系统特定状态轨迹移动，根据状态空间的位置不断修改运动路径，使其从一个区域移动到相邻区域不断切换，最终沿着预定路径紧密高频切换运动.

取PMSM 的系统状态变量为：

式中：ω*为给定的电机转速常量，ωr为实际转速.

根据式（14）、式（15）和式（16）写出状态方程为：

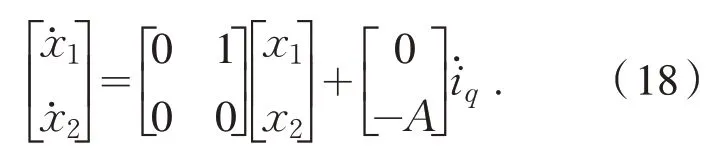
加入状态变量的积分量后，系统的滑模面的切换函数为：

式中c为大于0 的积分常数.

对式（19）中的s求导得：

为了加快系统的相应速度，减弱滑模抖动，利用指数趋近率设计滑模控制器以获得控制率，根据式（20）可得：

结合式（18）和式（21）得出速度控制器的控制率表达式为：

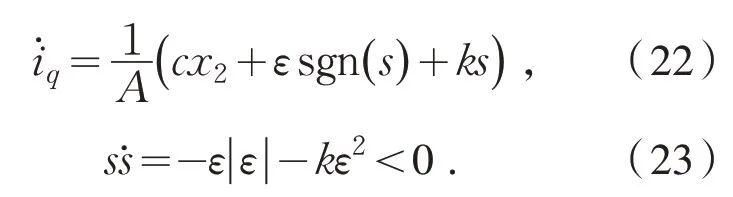
因此，设计的滑模面满足Lyapunov 稳定性条件.

4 系统仿真

风力发电系统主要由风速模型、风力机模型、传动系统模型以及永磁同步发电机模型构成.为保证仿真结果的准确性，将基本风的风速峰值设置为6 m/s，阵风的风速峰值设置为4 m/s，渐变风的风速峰值设置为8 m/s，随机风的风速平均值设置为1 m/s，方差设置为0.5，随机种子数设置为1，采样时间设置为0.001 s，则各类风速仿真结果如图2 所示.

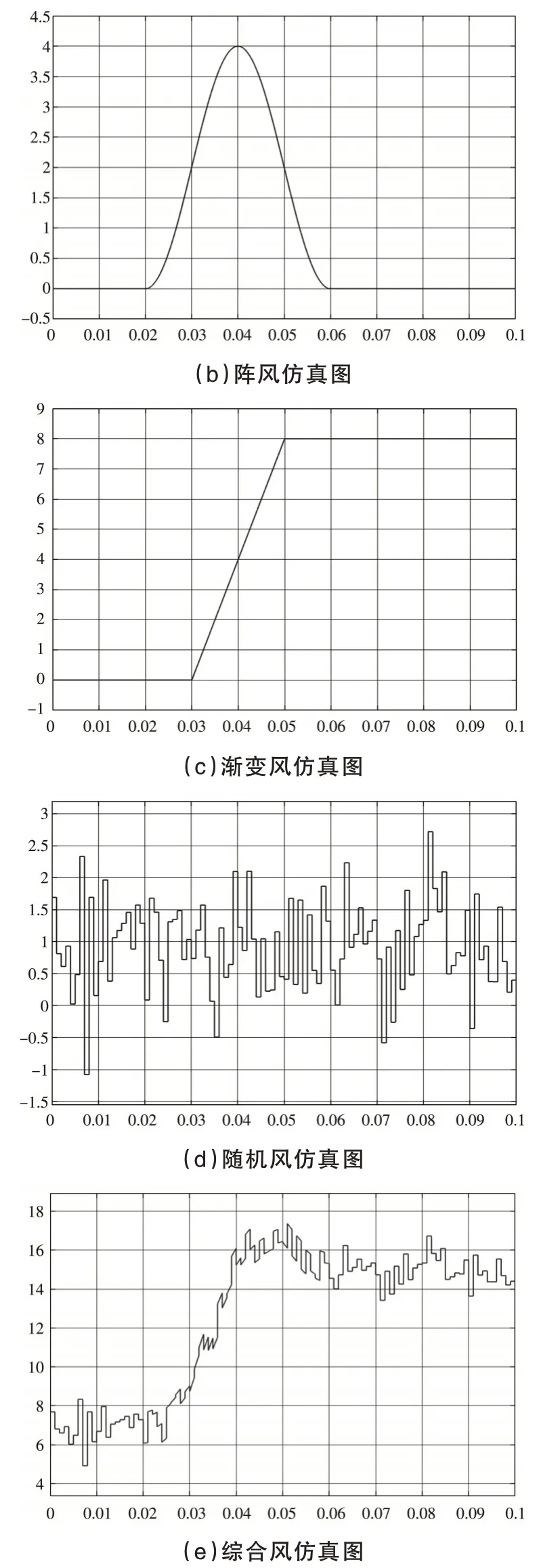
图2 各类风速仿真图

如图2 所示，基本风、阵风、渐变风、随机风仿真波形数据与设定值相符，图2（e）为四种风叠加后的综合风仿真图，可以发现综合风的仿真波形与渐变风的仿真波形相似，渐变风对于综合风速波形的影响较大，四分量法得到的综合风速波形图与渐变风的波形图相似，四种风速叠加得到的综合风的波形不再是平滑的，而是带有或大或小的毛刺干扰.

如图3 所示，与传统PI 控制相比，电磁转矩波形采用滑模变结构自寻优控制能更加平稳地达到稳定状态，最终沿着特定状态不断移动.

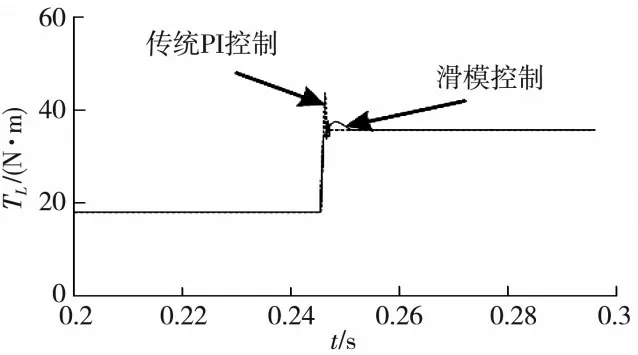
图3 电磁转矩波形图

由于PMSM 的转速正比于感应电势，转速越快，感应电势也越大，由此可知，d轴电压和q轴电压的波形与转子角速度的波形图有相似的趋势，在同时达到峰值并忽略风力机和发电机转轴的阻尼系数时，得到永磁同步发电机输出波形，如图4 所示.

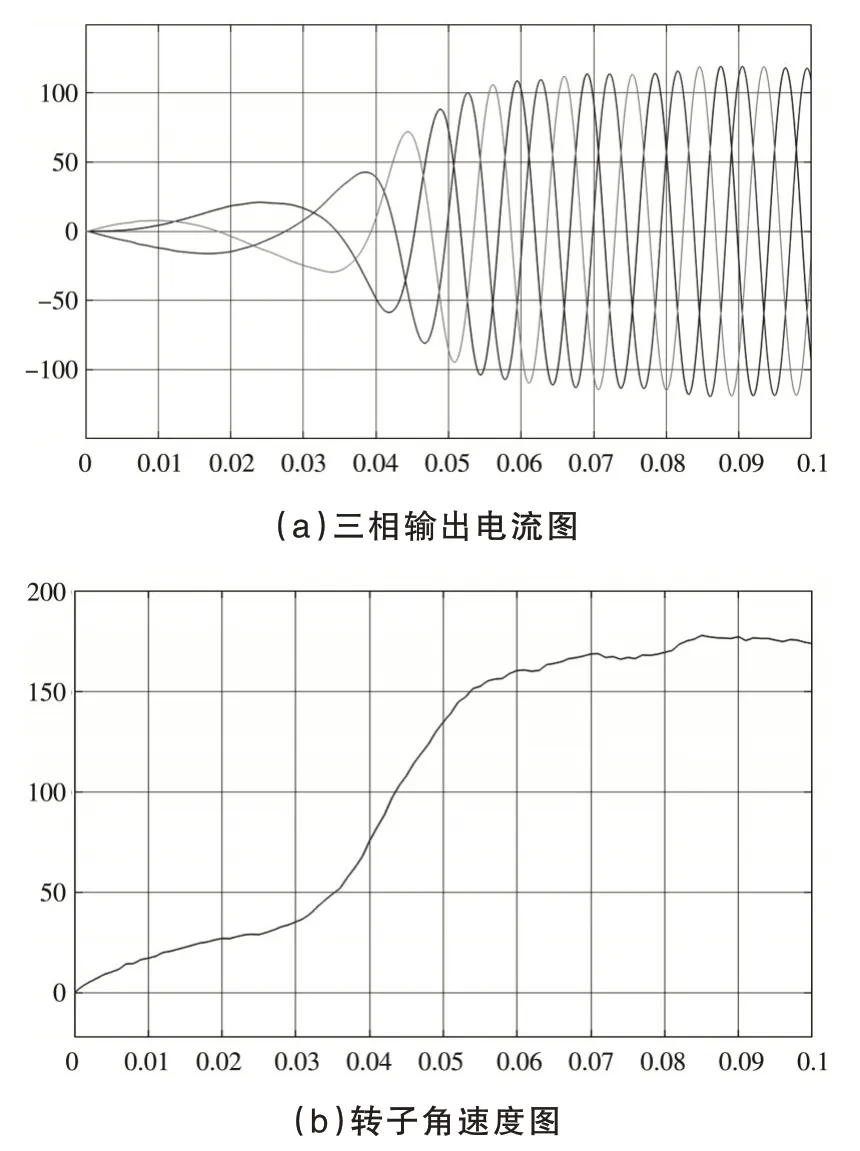
图4 永磁同步发电机输出波形图

由图4 可知，发电机转子角速度的波形比综合风的波形曲线光滑，发电机转子角速度波形波动不大，趋于平缓，而转子角位置波形在0.03～0.06 s 这段时间内斜率陡增，之后波形斜率趋于快速稳定.

5 结语

本文通过完善各类风速的数学模型，在Matlab/Simulink 环境下建立综合风模型，采用滑模变结构控制方法，使PMSM 在保证系统稳定性的前提下能够快速响应，比传统PI 控制平稳，仿真结果进一步指出，在复杂风速条件下，对永磁同步电机采用滑模变结构控制具有响应速度快和稳定性强等优点，提高了电机的发电效率.