变参数WGMRES(m)算法解线性方程组
2020-07-29白雪婷杨琴乐
白雪婷,杨琴乐
广义极小残余算法(GMRES)是求解由科学和工程问题得到的大规模稀疏线性方程组Ax=b最常用的方法之一,具有广阔的应用前景[1-2].实际应用中存在着许多对标准的GMRES 改进后的算法[3-4].其中 WGMRES 算法就是一种对GMRES 改进后的算法,由ESSAI于1998 年提出.该方法用D 内积来代替欧氏内积,由此即可通过加权Arnoldi 过程来加快那些远离零的残余向量的收敛,进而改善GMRES(m)的收敛性[5]. 为了进一步提高WGMRES 算法收敛性,SABERI 和 NAJAF 提出快速 GMRES 算法[6].丁伯伦和陈光喜提出微变形 WGMRES 算法[7].杨圣炜和卢琳章研究的加权Simple GMRES 算法则是以Simple GMRES 算法为基础,结合WGMRES 得到的,该方法计算量小于 WGMRES 算法[8].
在实际执行WGMRES(m)算法时,选取合适的加权因子可以加快算法收敛.此外,参数m的选择对算法的收敛性也尤为重要,m选择过小容易出现收敛慢甚至不收敛的现象,m选择过大会造成存储空间的浪费.基于此,文章首先给出一种新的加权因子,然后通过对原理型GMRES 算法和循环型GMRES算法的深入研究,指出适当的变化参数m可以改善GMRES 的收敛性,而且在一定程度上可以有效避免m取值过小或过大带来的一些弊端.
1 预备知识
考虑线性方程组

其中 :A∈Rn×n为非奇异大型矩阵 ,x,b∈Rn.取任意向量x0∈Rn,令x=x0+z,则有等价方程组

其中:r0=b-Ax0是初始残量.
给定m>0 ,取m维子空间Km=span{r0,Ar0,…,Am-1r0} ,Lm=AKm,基分别为其中vi,wi∈Rn. 利用Galerkin 原理取zm∈Km,使 (r0-Azm)⊥Lm,即(r0-Azm,wi)=0 ,这就构成 GMRES 算法 .
定义1 设D={d1,d2,…,dn} 是一个对角矩阵,di>0(i=1,2,…,n),称di为加权因子.取任意向量u,v∈Rn,则它们的内积可记为:
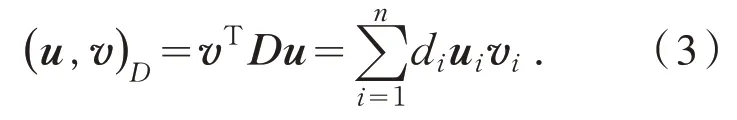
相应的加权范数定义如下:
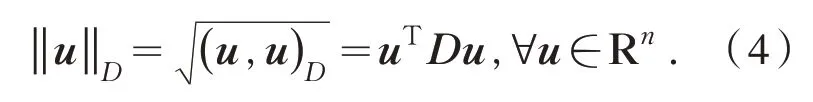
加权Arnoldi 过程如下:
①取v1=r0‖r0‖D;
②对于k=1,2,…,m,计算
③如果hk+1,k=0 ,则停止,否则
引理 1[5]向量v1,v2,…,vm构成子空间Km={v1,Av1,…,Am-1v1} 的一组D正交基.
引 理 2[5]令Vm=(v1,v2,…,vm)是n×m矩阵,Hm是m×m上海森伯格矩阵,其非零元由算法确定,则有

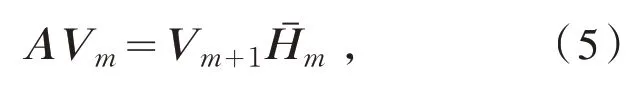
2 主要结果
2.1 WGMRES(m)算法
WGMRES(m)算法定义了新的内积,旨在通过加权Arnoldi 过程加快那些远离零的残余向量的收敛.因此,对角矩阵D=diag(d1,d2,…,dn) 中的元素di即加权因子d的选择是决定WGMRES(m)算法收敛快慢的重要因素之一.ESSAI 建议选取加权因子D=diag(d1,d2,…,di) ,其中 (r0)i表示残余向量r0的第i个元素.这样,‖d‖2=n,且当所有di都相等时向量D-范数就变成欧氏范数.显然,当 ‖r0‖→0 时,计算di比较困难.
文章给出一种新的加权因子,当线性方程组的系数矩阵A的阶数为偶数时,取其中i=1,2,…,n-1 ,当系数矩阵A的阶数为奇数时,取其中i=1,2,…,n-1 ,dn=1. 此时仍有
WGMRES(m)算法步骤:
①选择x0∈Rn,m∈N+(m<n).给定误差上界ε>0 ;
②选取di(i=1,2,…,n),使得计算r0=b-Ax0,v1=r0β,β=‖r0‖D;
⑤计算zm=Vm ym,xm=x0+zm;
⑥若 ‖rm‖=‖r0-Azm‖<ε,则迭代终止,否则x0=xm,转向②.
2.2 VRP-WGMRES(m)算法
原理型GMRES 算法表明参数m的取值越靠近系数矩阵A的阶数n,得到的解越接近方程组(1)的精确解.但是,不难看出,当n>>1 时,若仍取m≈n,将引起存储空间的过多需求,这是不现实的.循环型GMRES(m)算法建议选用一个固定的适当大小的参数m来完成GMRES(m),通过多次迭代可得方程组近似解,这在一定程度上克服了使用原理型GMRES 算法求解方程组时所面临的困难.但在实际执行GMRES(m)算法时,参数m取值过小可能出现收敛慢甚至不收敛的情况,如何选取一个理想的m至今未给出合理建议.本文以WGMRES 为基础,结合原理型GMRES 和循环型GMRES(m)的优点,提出VRP-WGMRES(m)算法,该算法中参数m可以取一个较小初值.
VRP-WGMRES(m)算法思想:适当变化参数m,通过迭代使 ‖rm‖=‖r0-Azm‖<ε.
VRP-WGMRES(m)算法:
① 选择x0∈Rn,m∈N+(m<<n). 给定误差上界ε>0 ;
②选择di(i=1,2,…,n),使得计算r0=b-Ax0,v1=r0β,β= ‖r0‖D;
⑤计算zm=Vm ym,xm=x0+zm;
⑥若 ‖rm‖=‖r0-Azm‖<ε,则迭代终止,否则x0=xm,m=m+1(m≤n),转向②.
3 数值算例
分别用 GMRES(m),WGMRES(m)和DGMRES(m)三种算法求解线性方程组(1).图1和图3中1-WGMRES(m),2-WGMRES(m)分别表示加权因子d取文献[4]中所给值和本文所给值时对应的WGMRES(m)算法.图2和图4 中WGMRES(m)表示加权因子d取本文所给值时对应的算法.
算例1 考察单位正方形区域 Ω={(x,y)|0 <x,y< 1} 上 Possion 方程
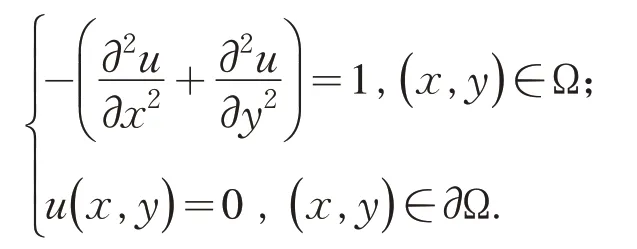
用正方形网格h=0.02 来求解上述问题.采用五点差分格式离散后可得线性方程组Ax=b,其中A为对称矩阵.取初始向量x0=(0 ,0,…,0)T,给定误差为 ε=1.0e-10.图 1 给出了m=6时,1-WGMRES(m)和2-WGMRES(m)的收敛关系图.图2给出了m=6时,GMRES(m),WGMRES(m)和DWGMRES(m)三种算法的收敛关系.表1 和表2 给出了当重启动参数m取不同值,残量范数达到给定误差时三种算法的数值结果.
从图1 可以看出,当加权因子d取本文所给值时,WGMRES(m)收敛且速度较快,这既说明文章选取的加权因子优于文献[4]中所给的加权因子,又表明本文提出的加权因子是合理的.

图1 加权因子d 取不同值时收敛关系图

图2 三种算法的收敛关系图
从表1 可以看出,当残量范数达到给定误差时,对最初给定的m,DWGMRES(m)算法收敛最快;当参数m发生微小变化时,GMRES(m)的迭代次数波动较大,WGMRES(m)次之,DWGMRES(m)变化最小,这说明本文提出的新算法有很好的稳定性.此外,不难发现,当最初给定的参数m取值较小时,新算法有更快的收敛速度和更高的计算精度.这表明使用文中所给算法求解方程组得到的近似解更接近精确解.
算例 2[6]求解线性方程Ax=b,选择b使得x=(1 , 1,…,1)T是Ax=b的解,矩阵A为:
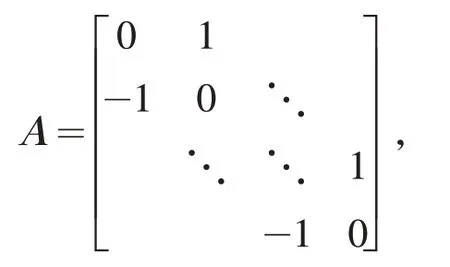
取初始向量为x0=(0 ,0,…,0)T,给定误差为ε=1.0e-6.图 3 给出了当n=100,m=10 时 1-WGMRES(m)和2-WGMRES(m)的收敛关系图. 图 4 给出了当m=10 时,GMRES(m),WGMRES(m)和DWGMRES(m)的收敛关系.表3 和表4 给出了当残量范数达到给定误差,重启动参数m取不同值时,三种算法的数值结果.

图3 加权因子d 取不同值时收敛关系图

表1 ε =1.0e-10 且m 取不同值时三种算法迭代次数比较

表2 ε =1.0e-10 且m 取不同值时三种算法计算精度比较

表3 n =100,ε =1.0e-6 且m 取不同值时三种算法迭代次数比较

表4 n =100,ε =1.0e-6 且m 取不同值时三种算法计算精度比较
从图3 可知,当加权因子d取本文所给值时,WGMRES(m)收敛,当加权因子d取文献[4]中的值时,WGMRES(m)算法失败,只能得到初始残量从图4和表3、表4可知,文章所提出的DWGMRES(m)算法有更好的稳定性、更快的收敛速度以及更高的计算精度,可以用DWGMRES(m)算法来求解方程组.

图4 三种算法的收敛关系图
4 结论
针对WGMRES(m)算法,本文给出了一种新的加权因子,并验证了其合理性和有效性.通过对WGMRES(m)算法中参数m作适当变化,提出了DWGMES(m)算法,数值试验结果表明新方法的稳定性,收敛速度以及计算精度优于GMRES(m)和WGMRES(m)算法,并可以有效地避免参数选择较小时GMRES(m)算法收敛慢甚至不收敛的现象.
