显含阻尼项的二阶非线性中立型Emden-Fowler微分方程的振动性和渐近性
2020-07-28仉志余宋菲菲俞元洪
仉志余,宋菲菲,俞元洪
(1.太原工业学院理学系,山西 太原030008;2.中国科学院数学与系统科学研究院,北京100190)
1.引言
来源于数学物理方程的Emden-Fowler型微分方程的研究成果已被广泛应用在天体物理、气体动力学、物理化学以及各高新技术领域之中[1−4].例如带阻尼项的二阶Emden-Fowler方程


其中z(t)=x(t)+g(t)x(τ(t)),r ∈C1([t0,∞),(0,∞)),p,q ∈C([t0,∞),[0,∞)),α>0,β >0为常数,在0≤g(t)≤1,p(t)≥0,q(t)≥0,r′(t)>0等基本假设条件下,获得了多个振动定理,推广了上述有关文献的部分结果.
通过以上分析不难看出,方程(1.1)、(1.3)-(1.10)均为方程(1.2)的特殊类型,而且它们所谓的阻尼项系数(例如(1.6),(1.7)中的r(t)和(1.8)-(1.10)中的p(t))和中立项系数(例如(1.3)-(1.5)、(1.9)、(1.10)中的r(t)和(1.6)-(1.8)中的a(t))的导数都是非负函数.但是,不难发现,这些方程中显含的阻尼项并不代表实际物理意义下的全部阻尼项.因为由文[30] 知,当r(t)>0,r′(t)≥0时,二阶微分方程


因此,对于方程(1.2),本文将总假设以下条件成立:
(H1)r′(t)+g(t)≥0 且0≤p(t)≤p0<∞.
(H2)τ ◦σ=σ ◦τ,τ′(t)≥τ0>0.
(H3) 存在不恒为零的函数q ∈C([t0,∞),[0,∞)),满足f(t,u)/u≥q(t)≥0,u≠0,t ≥t0.
其次,本文将引进指数函数变换,并借助于Riccati变换,积分平均和不等式技巧研究方程(1.2)的振动性和渐近性,建立新的振动准则,顺便导出方程(1.1)新的振动性渐近性判据.
下面,引入指数函数变换

用φ(t)乘以方程(1.2)的两端,则(1.2)变为等价的不显含阻尼项的微分方程
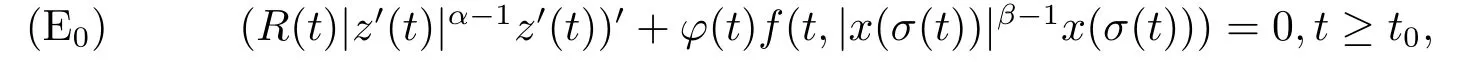
其中R(t)=r(t)φ(t).
我们通过方程(E0),在两种情形∫

下,分别讨论方程(1.2)的振动性和渐近性,为此先给出以下几个引理.
引理1.1设(H3)和(1.13) 式成立.如果x(t)是方程(1.2)的最终正解,则最终有z′(t)>0.
证 因为x(t)是方程(1.2)在[t0,∞) 上的最终正解,则存在t1≥t0,使得当t ≥t1时有x(t)>0,x(τ(t))>0,x(σ(t))>0,由(H3)和(E0),我们得到
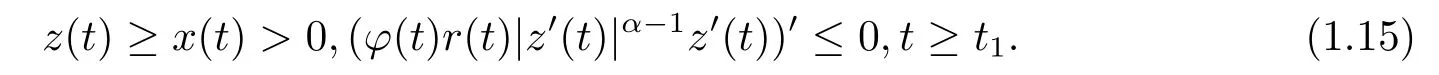
因此φ(t)r(t)|z′(t)|α−1z′(t) 是非增函数且z′(t)最终保号,于是z′(t) 仅有两种可能.我们断言z′(t)>0,t>t1.否则,假设z′(t)≤0,t>t1.由(1.15)式知,存在常数K >0 使得
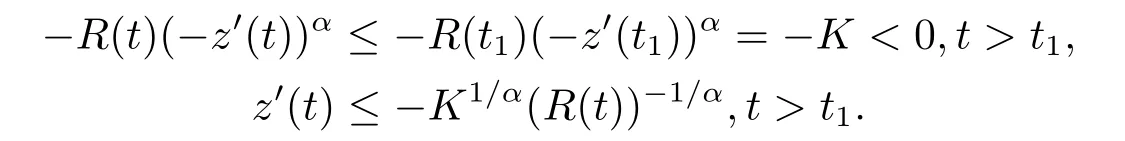
从t1到t积分上式,我们得到
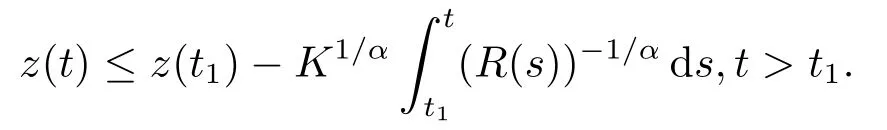
在上式中令t →∞,由条件(1.13)得z(t)→−∞.此式与(1.15)式矛盾,故结论成立.证毕.
引理1.2设A>0,B ≥0,λ>0且均为常数,则当u>0 时,有
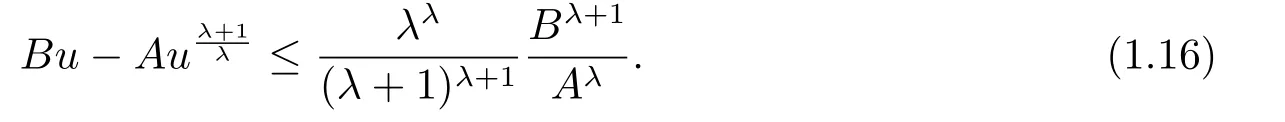
引理1.3设X >0,Y >0,λ>0为任意实数,则有

当且仅当X=Y,λ ≥1时第一式等号成立.
2.主要结果
为建立方程(1.2)振动性渐近性准则,引入以下记号:
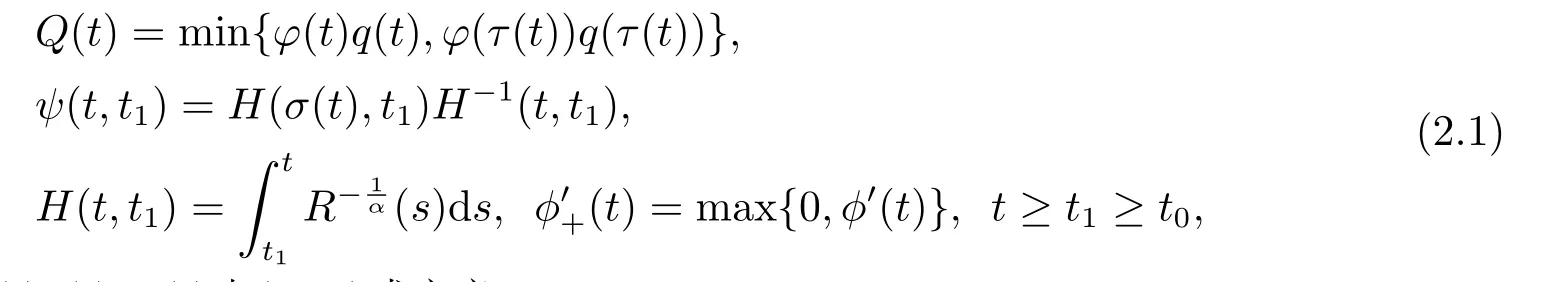
其中R(t)=φ(t)r(t),φ(t)由(1.12)式定义.
定理2.1设(H1)-(H3)和条件(1.13)式成立.如果存在函数ρ ∈C1([t0,∞),(0,∞))和t2≥t1≥t0,使得当t ≥t2时σ(t)≥t1,并对任意常数m ∈(0,1] (当α=β时,m=1),恒有

成立,其中Cβ,Q(t)和ψ(t,t1)分别由(1.17)和(2.1)式定义,则方程(1.2)振动.
证假设x(t)是方程(1.2)的非振动解.不失一般性,设x(t)为[t0,∞)上的最终正解(x(t)<0的情况类似可证),则存在t2≥t1≥t0,使得t ≥t1时,有x(t)>0,x(τ(t))>0,x(σ(t))>0,当t ≥t2时,有σ(t2)≥t1.于是,由方程(1.2)的等价方程(E0)得不等式
(R(t)(z′(t))α)′+Q(t)f(xβ(σ(t)))=0,
可得
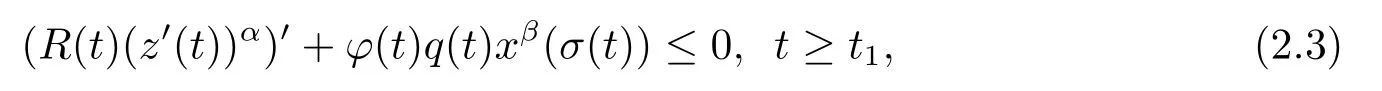
以及
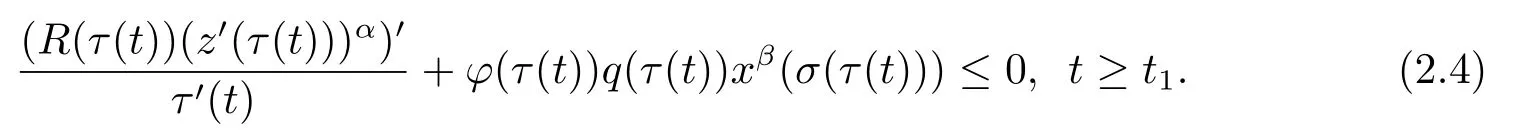
结合(2.3)和(2.4)式,并注意到σ ◦τ=τ ◦σ,z(t)≤x(t)+p0x(τ(t))以及引理1.3,得

根据引理1.1知,不妨设z′(t)>0,t ≥t1.于是,对于α,β的取值,分两种情形讨论如下:
情形1α ≤β,这时,λ=α.作Riccati变换

则w(t)>0,t ≥t1.对(2.6)式求导并注意到τ′(t)≥τ0>0,得
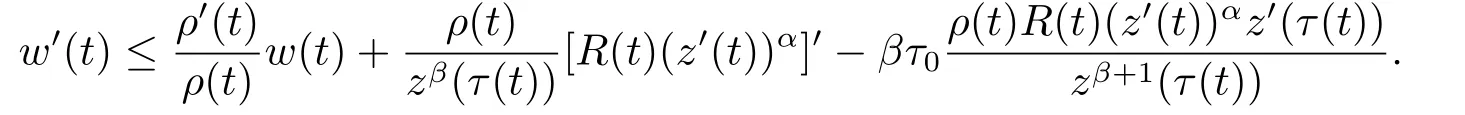

结合(2.8)和(2.10)式,并注意到(2.5)式及z′(t)>0,得

注意到这时λ=α,γ=1,mα ∈(0,1].所以,上式与(2.2)式矛盾.
情形2α>β
作形如(2.6)式的Riccati变换,则(2.7)式仍成立.由于R(t)(z′(t))α >0单调减,所以,当t ≥t1时,有R(t)(z′(t))α ≤m1=max{R(t1)(z′(t1))α,1}.则m1≥1,又有
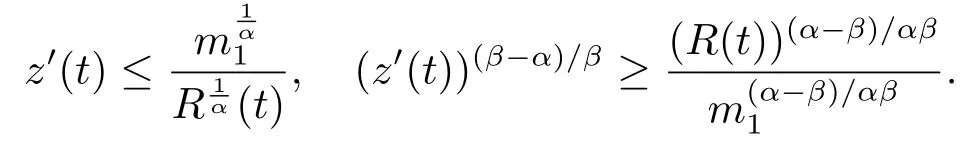
将上式代入(2.7)式并利用引理1.2的(1.16)式,得

在文[7]中,LI和Rogovchenko对于方程(1.3)限定β >α=1时,就τ(t),σ(t)与t大小比较的多种情形,获得了多个振动定理3.1-3.8.例如其定理3.3,因为这时(H3)自然满足,所以,可以改述为
定理2.2(LI-Rogovchenko定理) 设(H1),(H2),σ(t)≤τ(t)≤t.若有
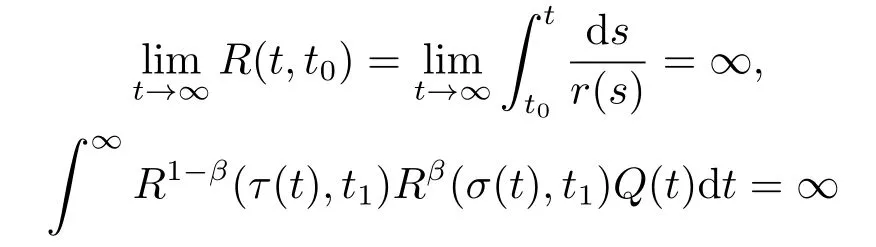
均成立,则方程(1.3)振动.
特别在本文定理2.1中取函数ρ(t)为非零常数,则立即可得类似的L-R型振动定理如下.
推论2.1(LI-Rogovchenko型振动定理) 设(H1)-(H3)和条件(1.13)式成立.如果存在t2≥t1≥t0,使得当t>t2时有σ(t)≥t1和
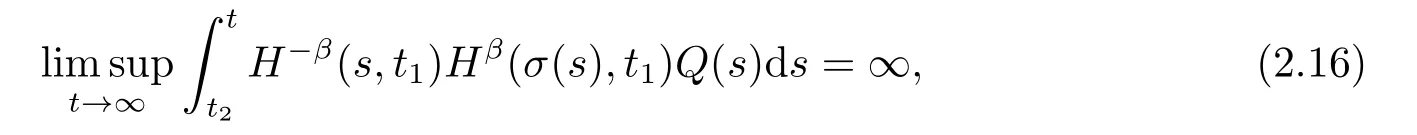
其中H(t,t1),Q(t)如(2.1)式定义,则方程(1.2)振动.
注2.1易知,本文推论2.1又是著名Leighton振动定理[33](即当=∞时,方程(r(t)x′(t))′+q(t)x(t)=0 振动)的自然推广,但是文[7]的诸定理不能还原到Leighton振动定理,因为其中的β >1.
注2.2显然即使当方程(1.2)退化成不显含阻尼项的方程(1.5)或(1.3)时,本文推论2.1也是新的,本文定理2.1也统一了文[2](其中α=β)定理4和定理5的形式.同时本文定理2.1已完全包含和改进了文[27]的定理1,因为从其证明中可以看出,定理1中的η >0,η1=a(t1)(z′(t1))λ >0均应该是任意正常数方可,而本文定理2.1中对应的任意常数为m ∈(0,1] (特别,当α=β时,m=1) 更严谨更精确.此外,对于如下例2.1,本文所列文献及其引文均无效,可见本文定理2.1及其推论2.1 的效果.
例2.1考虑方程
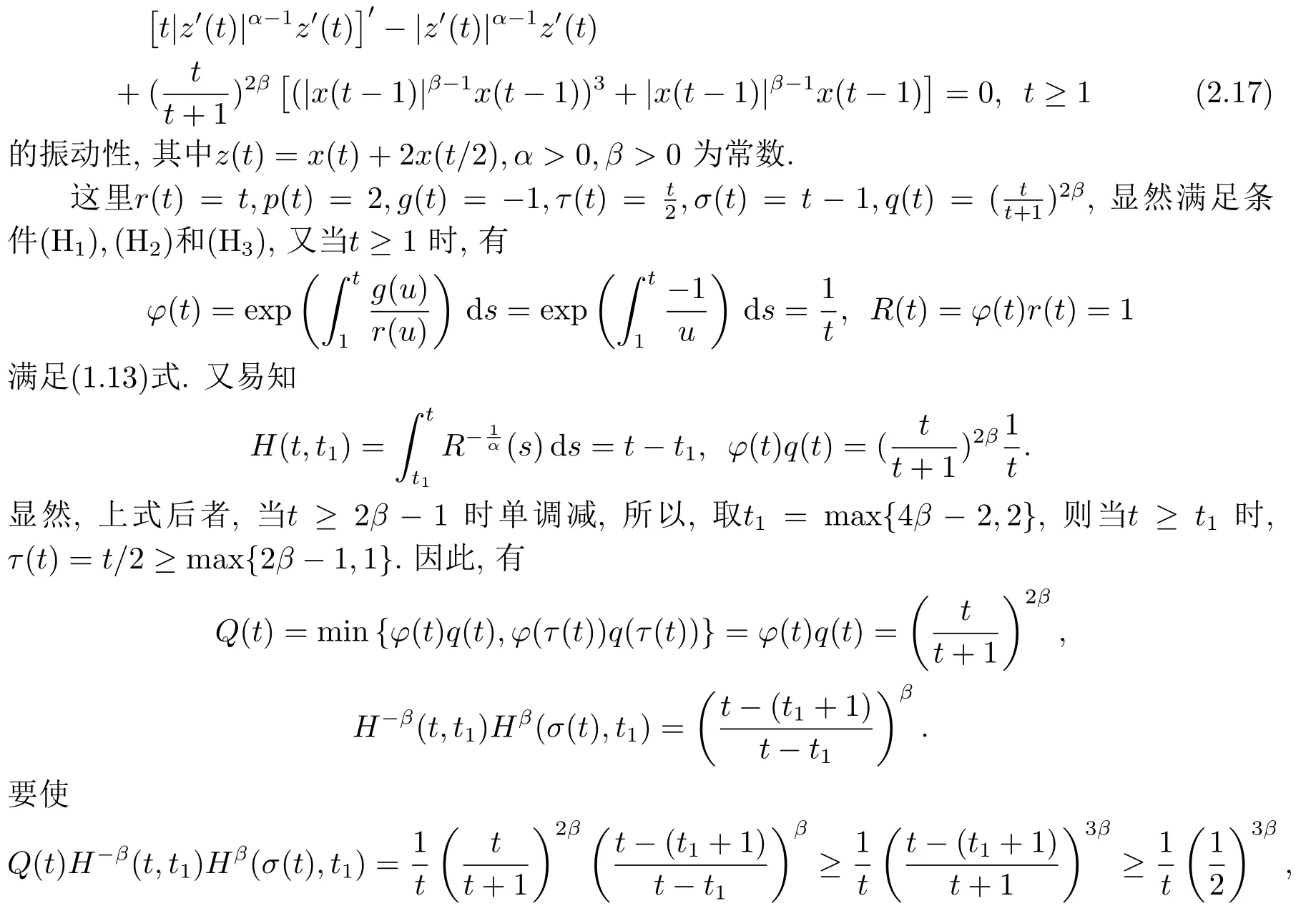


和

均成立,其中φ(t) 由(1.12)式定义,H(t,t1),Q(t)如(2.1)式定义,则方程(1.2)的每一个解x(t)振动或.
例2.2讨论方程

所以,(2.21)式也成立.故由推论2.2知,方程(2.22)的每个解x(t)振动或.
例2.3讨论方程
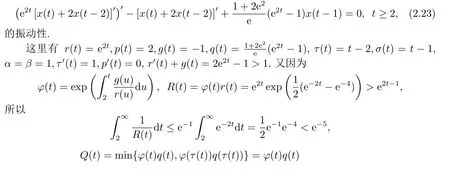


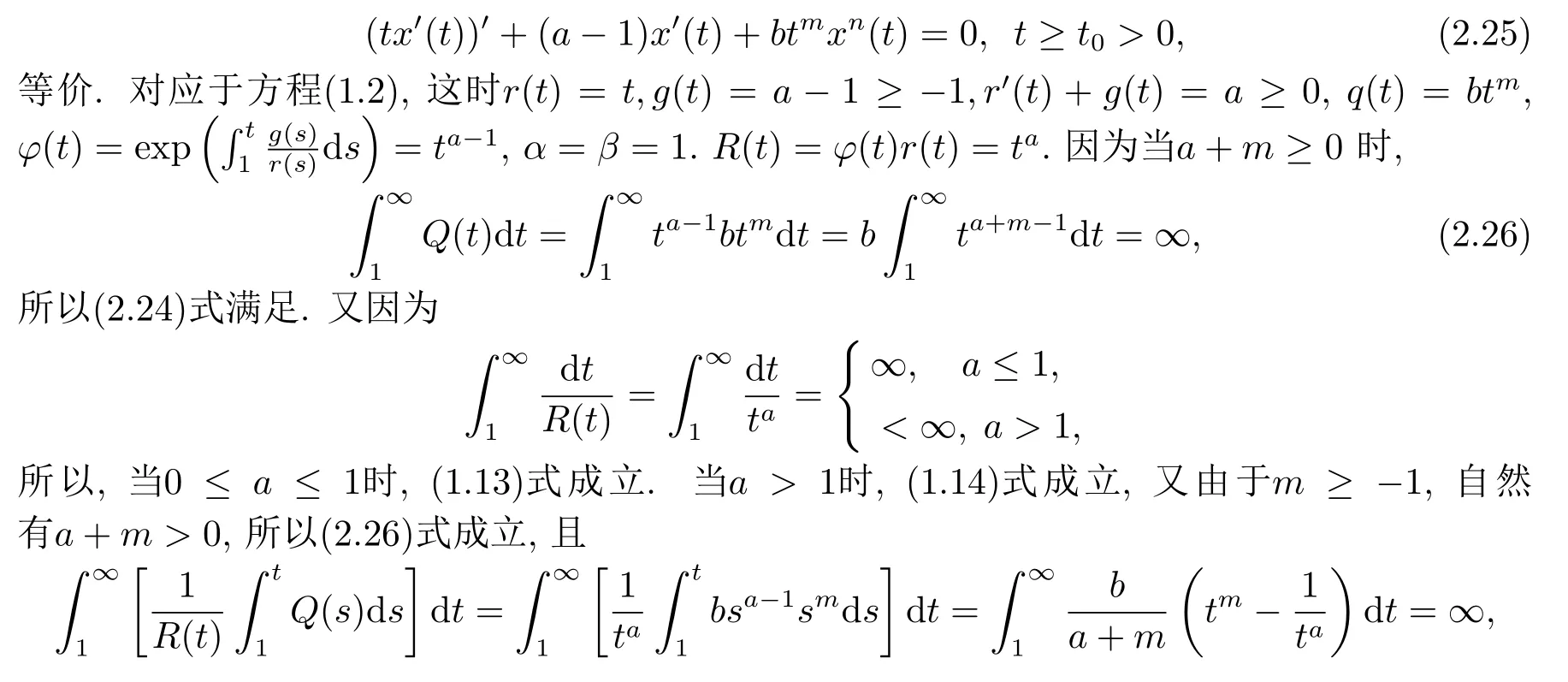

猜你喜欢
杂志排行
应用数学的其它文章
- 具有惯性项和阻尼项的Cahn-Hilliard方程的整体吸引子
- 一角点支撑对面两边固支正交各向异性矩形薄板弯曲问题的辛叠加解
- Positive Solutions for Fractional Differential Equations with Integral and Infinite-Point Boundary Conditions
- Comparison Principle of Very Weak Solutions for Nonhomogeneous Elliptic Equations
- Global Existence,Asymptotic Behavior and Uniform Attractor for a Non-Autonomous Thermoelastic Timoshenko System of Type I with a Memory Term
- A m,p-Laplacian Parabolic Equation with Nonlinear Absorption and Boundary Flux
