具有惯性项和阻尼项的Cahn-Hilliard方程的整体吸引子
2020-07-28史苑任永华
应用数学 2020年3期
史苑,任永华
(太原理工大学数学学院,山西 晋中030600)
1.引言
考虑下面具有惯性项和阻尼项的Cahn-Hilliard方程

20世纪60年代末,Cahn和Hilliard提出了经典的Cahn-Hilliard方程,即ut−∆(−∆u+f(u))=0.Cahn-Hilliard方程是用来模拟合金等二元材料的相对分离过程的.为了将经典理论推广到强非平衡分解的情形,在文[2-3]中,作者通过在方程中加入惯性项εutt,提出了Cahn-Hilliard方程的双曲松弛.Khanmamedov和Yayla在文[1]中讨论在相应的初边值条件下弱解的适定性,且证明了整体吸引子的存在性.带有阻尼项的方程的吸引子在文[4-5,12]中也给出了严格的论证.近年来,很多研究者对Cahn-Hilliard方程产生了浓厚的兴趣,但在特殊边界条件下对带有阻尼项的双曲Cahn-Hilliard方程的研究仍无果.本文主要研究了在亚三次非线性二维情形下,带有阻尼项的双曲Cahn-Hilliard方程的解的适定性,并讨论了方程吸引子的存在性.另外由于特殊项−∆(βut)的出现及分数阶空间嵌入定理的处理使得工作更为复杂.
2.基本假设及主要结论


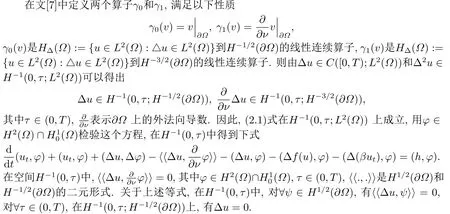

3.弱解的适定性




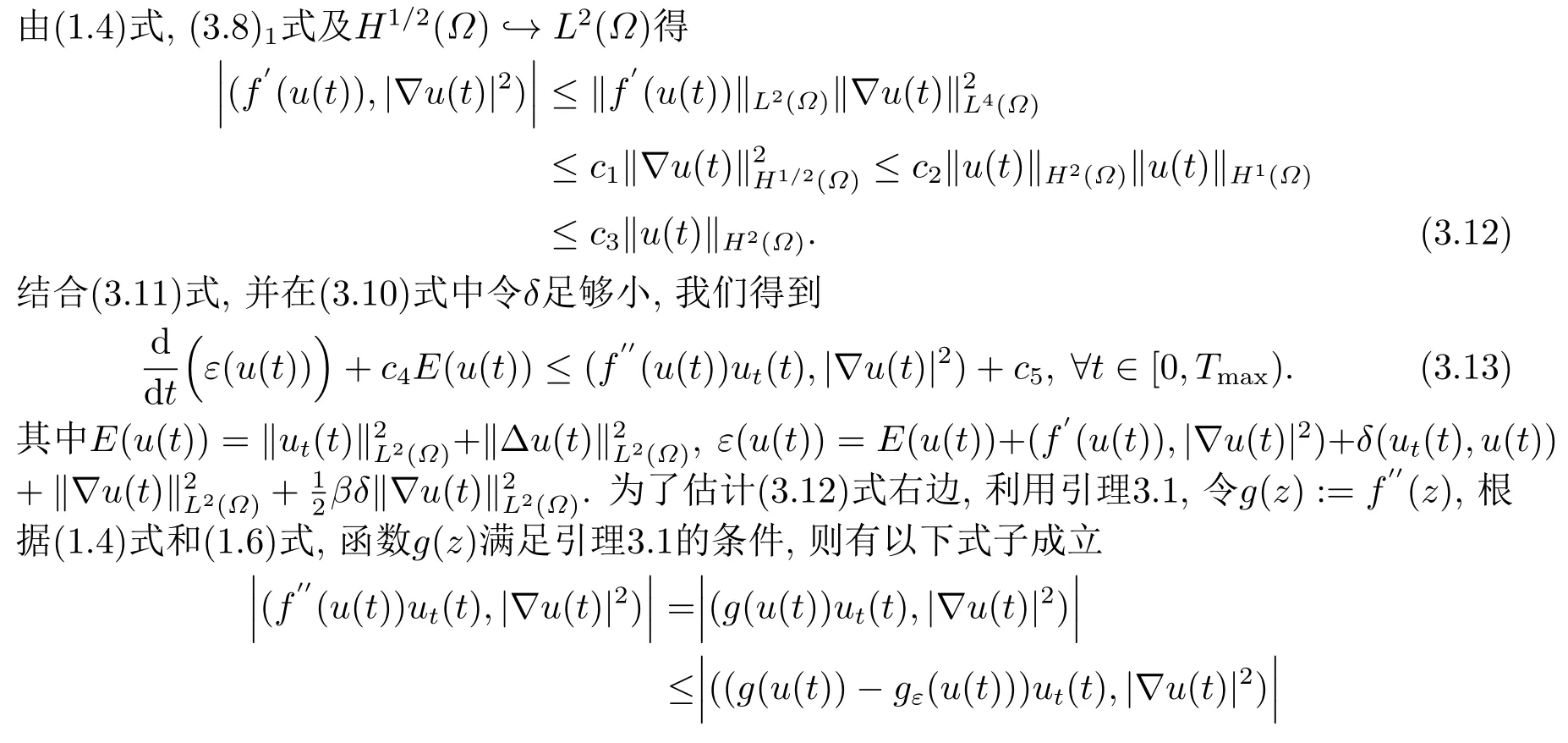

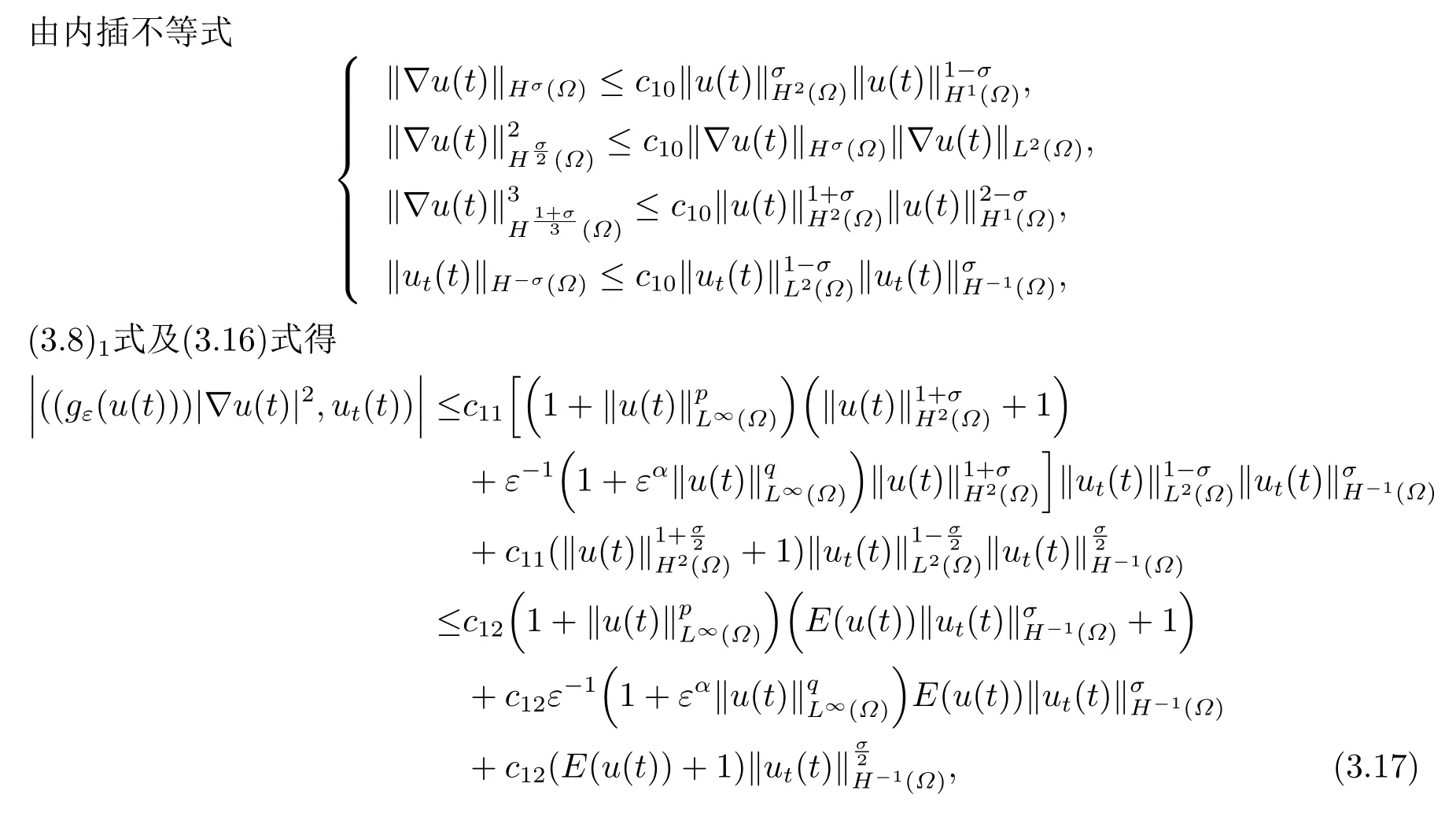





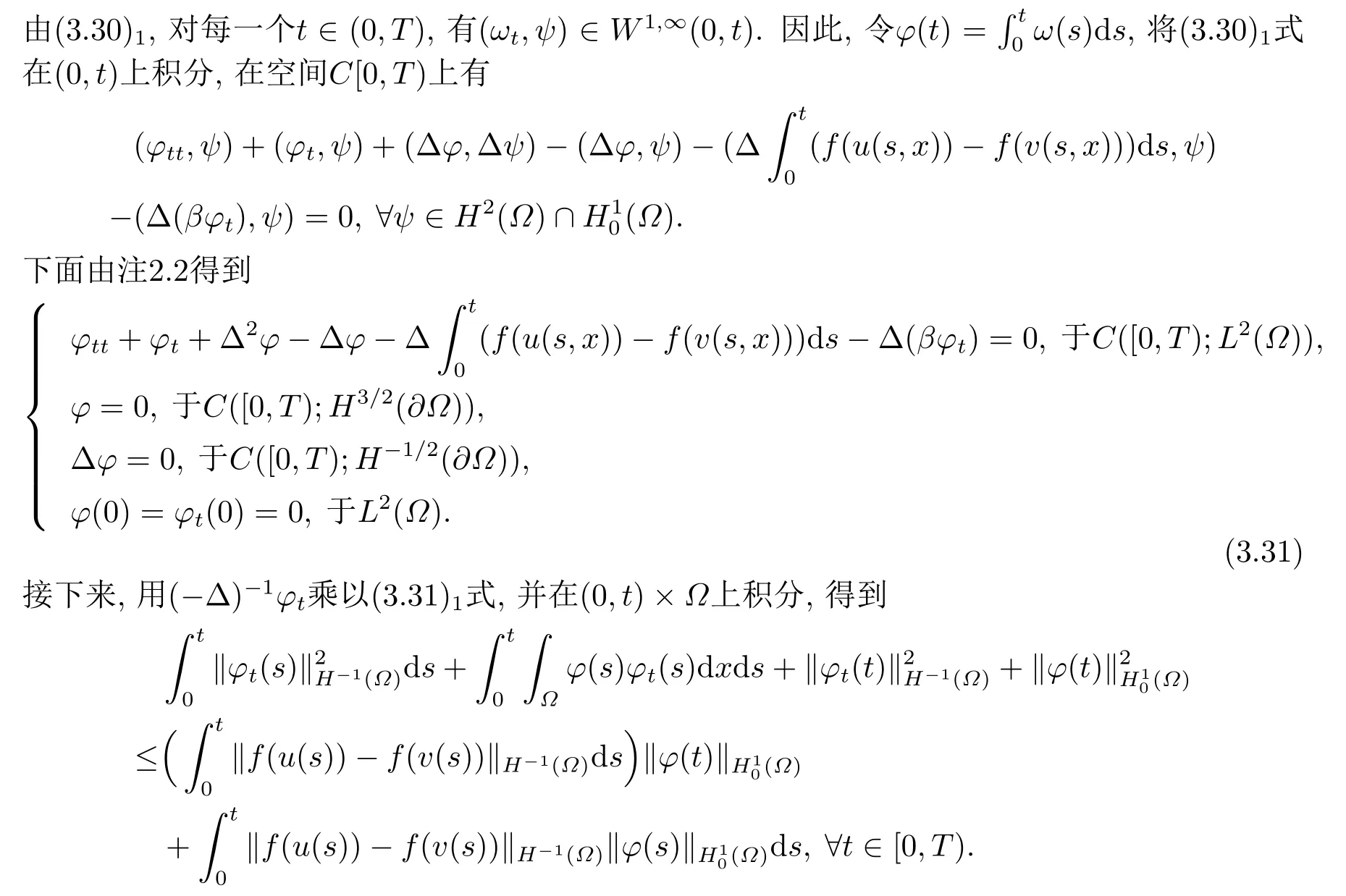

4.整体吸引子的存在性




