Comparison Principle of Very Weak Solutions for Nonhomogeneous Elliptic Equations
2020-07-28XIESuying谢素英YANGChao杨超
XIE Suying(谢素英),YANG Chao(杨超)
(College of Science,Hangzhou Dianzi University,Hangzhou 310018,China)
Abstract: Under some suitable assumptions,a comparison principle of very weak solutions for quasi-linear elliptic equation−divA(x,∇u) = f(x,u) is given by using McShane extension theorem to construct the Lipschitz continuous test function,and the corresponding results of some homogeneous equations are generalized.
Key words: Very weak solution;Comparison principle;Lipschitz continuous test function;McShane extension theorem
1.Introduction
In this paper,we study a comparison principle of very weak solutions to nonhomogeneous elliptic equation

In recent years,there exist many results of weak solutions for quasilinear elliptic equations.Gilbarg and Trudinger[1]established a comparison principle of classical solutions for secondorder quasilinear elliptic equation.Tolksdorf[2]generalized the results of [1] and obtained a comparison principle of weak solutions forDamascelli[3]studied a comparison principle of weak solutions(inW1,∞(Ω)) for−divA(x,∇u)=g(x,u) by taking an appropriate test function.The right hand side of the equation(i.e.lower order term)in [1-3] satisfied non-increasing foru.The definition of very weak solutions for A-harmonic equation were given[4],Iwaniec et al.[5]obtained the existence and local integrability of very weak solutions to the A-harmonic equation by using Hodge decomposition method.By Hodge decomposition method to construct a proper test function,the uniqueness of the very weak solutions of−divA(x,∇u)=f(x,u) is obtained under the condition of weak boundary value in [6].More references about Hodge decomposition see [7-9].
Lewis[10]and ZHONG[11]studied the existence and uniqueness of very weak solutions forDmA(x,Dmu)=0 and−divA(x,∇u) =µin Grand Sobolev space by using the method of maximal function to construct Lipschitz-type continuous test function.SHI[12]studied a comparison principle of very weak solutions to−divA(x,∇u)=0 by the similar method in [10-11].ZHU[13]introduced a comparison principle of very weak solutions for−divA(x,u,∇u) =f(x)+div(|∇up−2|∇u) by constructing a suitable test function,and combining Hardy-Littlewood maximum function et al.
However,the comparison principle of very weak solutions to equation (1.1) has not been studied yet.Inspired by [6,11-12],we study a comparison principle of equation (1.1) by using McShane extension theorem to contract the Lipschitz continuous test function.Compared with the right hand side in [13],ourf(x,u) in (1.1) is more general,the reason is that the right hand side of [13] is actuallyf(x) which is independent ofu.In particular,owing to the appearance off(x,u) in the proof,we apply Theorem 2.7 in [14] (i.e.Lemma 2.3 in this paper),Sobolev embedding theorem,Hölder’s and Young’s inequalities in order to estimate the integral term off(x,u).In this paper,we assumef(x,u) to be non-increasing foru,so that our result also holds in classical solution and weak solution cases.

2.Preliminary Lemmas and Main Result
In order to prove the main result,we need the following lemmas.

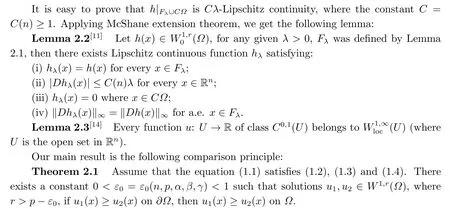
3.Proof of Theorem
In the following proof,all the constantsCmay change from line to line.
ProofLetu1,u2∈W1,r(Ω) are solutions of equation (1.1),andu1≥u2on∂Ω.We considerv(x)=min{0,u1−u2}and know thatv(x)∈W1,r0(Ω).From Lemma 2.1 and Lemma 2.2,there existsvλas Lipschitz continuous extension of functionv(x) onFλ ∪CΩ,andvλcan be used as a test function in Definition 1.1 because it satisfied (i)-(iv) from Lemma 2.2.Next we have


Multiplying both sides of the above inequality byλ−1−ε(0<ε <1) and integratingλon(0,+∞),we deduce that

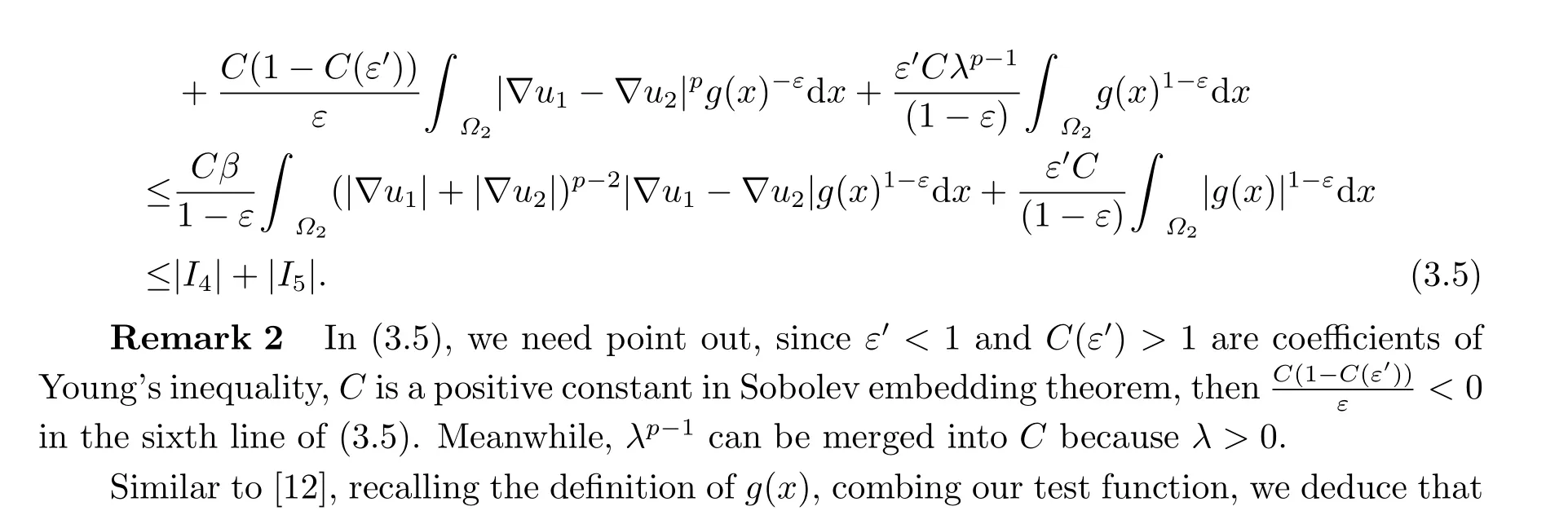

By using Hölder’s and Young’s inequalities,we obtain
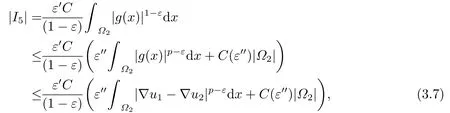
whereε′′andC(ε′′) stand for the small and large constants respectively from Young’s inequality.
Similar to [12],We distinguish the proof into two cases:
Case 1p ≥2.In this case,by using Hölder’s inequality we have

This is easy to implies
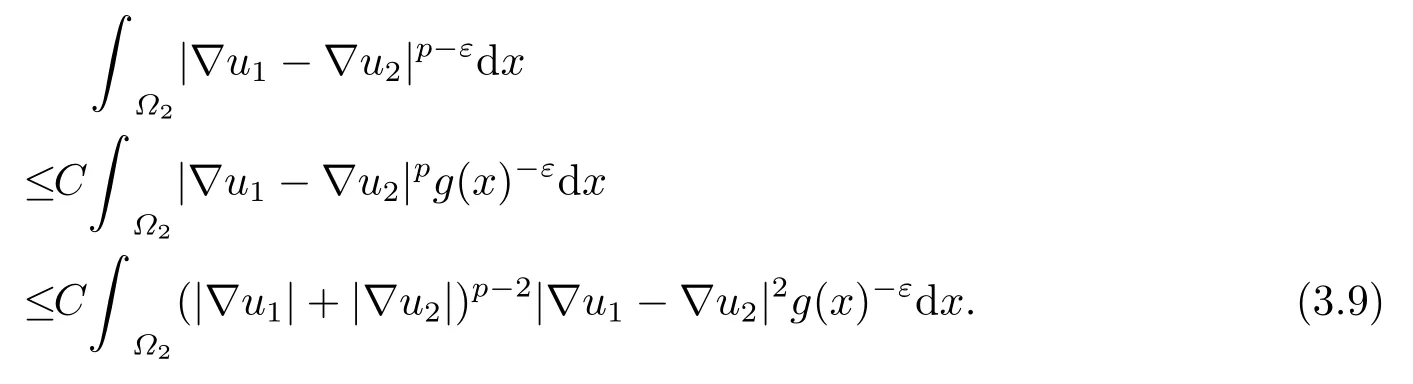
Combining (3.5),(3.6),(3.7),(3.8)and (3.9),we have

where the above inequality holds for all 0<ε ≤ε0<1,and C doesn’t depend onε.We letε →0,then we getu1=u2a.e.inΩ2and Theorem 2.1 were proved.
Case 21 that is, Combining (3.5),(3.6),(3.7) and (3.11),there have Similar to Case 1,we letε →0,and Theorem 2.1 is proved.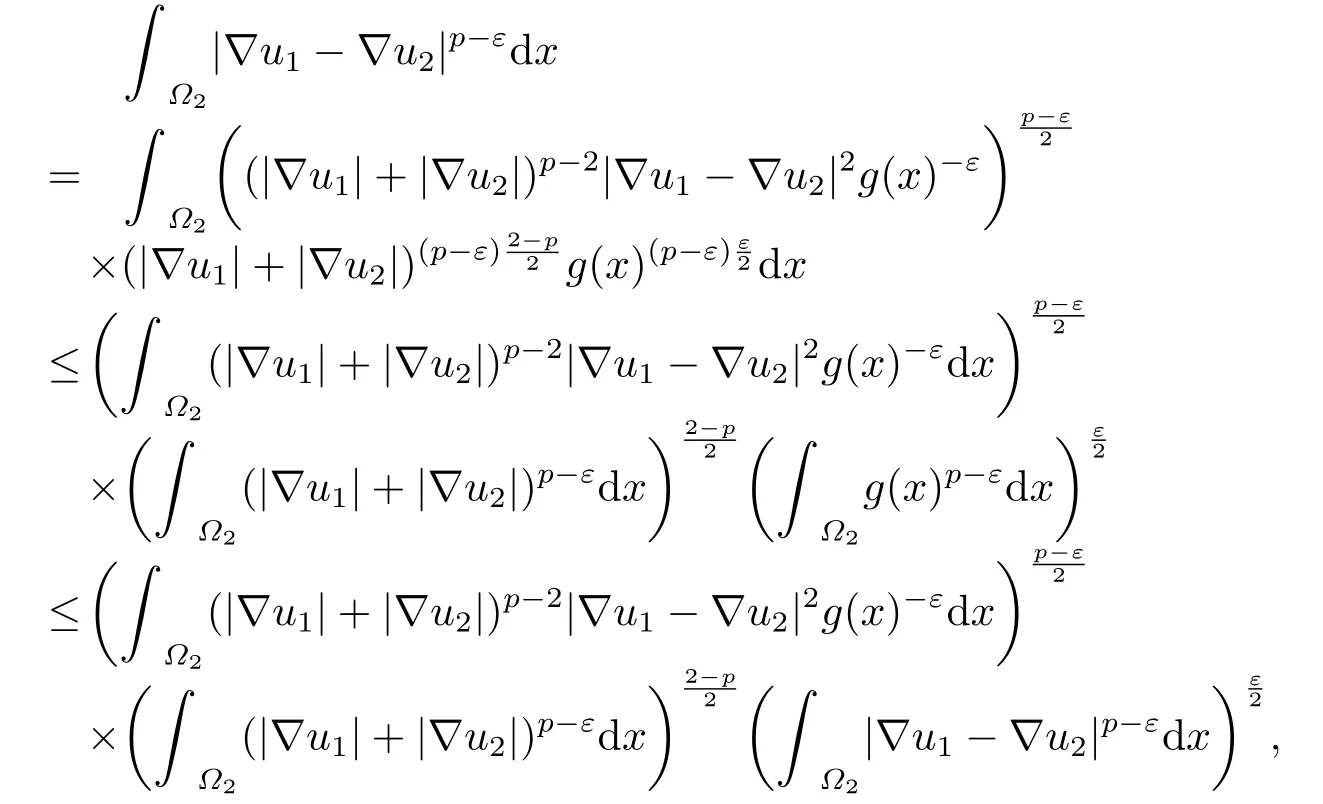


猜你喜欢
杂志排行
应用数学的其它文章
- 具有惯性项和阻尼项的Cahn-Hilliard方程的整体吸引子
- 一角点支撑对面两边固支正交各向异性矩形薄板弯曲问题的辛叠加解
- Positive Solutions for Fractional Differential Equations with Integral and Infinite-Point Boundary Conditions
- Global Existence,Asymptotic Behavior and Uniform Attractor for a Non-Autonomous Thermoelastic Timoshenko System of Type I with a Memory Term
- A m,p-Laplacian Parabolic Equation with Nonlinear Absorption and Boundary Flux
- Meromorphic Solutions of a Type of Complex Differential-Difference Equations
