偏序Menger PSM-空间中的耦合重合点定理

胡品,谷峰

(杭州师范大学理学院,浙江 杭州311121)

1.引言

1942年,Menger[1]用分布函数代替非负实数作为度量值,提出了Menger概率度量空间(简称Menger PM-空间)的概念.1960年,Schweizer与Sklar[2−3]在Menger PM-空间中引进t-范数,并讨论了该空间的一些性质.1994年,张石生等[4]对Menger PM-空间的一些重要性质进行了总结.2006年,Mustafa和Sims[5]提出了G-度量空间的概念,它是度量空间的一个推广.在此之后,Sedghi,RAO和Shobe[6]研究了由Dhage[7]提出的D-度量空间,同时引入了D∗-度量空间的概念.2012年,Sedghi和Aliouche[8]提出了S-度量空间的概念,它是G-度量空间与D∗-度量空间的一个推广.

2014年,ZHOU等[9]在G-度量空间和Menger PM-空间的基础上,引入了Menger概率G-度量空间(简称为MengerPGM-空间)的概念,并证明了几个不动点定理.之后,ZHU等[10−11]在MengerPGM-空间中引入了ϕ-压缩条件和映象对弱相容的概念,建立了若干公共不动点定理.2015年,Hasanvand和Khanehgir[12]提出了Menger概率b-度量空间(简称为MengerPbM-空间)的概念,并讨论了该空间中的不动点问题.

受上述研究工作的启发,本文提出一类新的概率度量空间―Menger PSM-空间,讨论了该空间的拓扑性质,证明了偏序Menger PSM-空间中新的耦合重合点定理,并给出了一个用以说明新结果有效性的实际例子.

2.预备知识

定义2.8设(X,S∗,∆)是一个Menger PSM-空间,{xn}是X中的序列,x ∈X.

引理2.3设(X,S∗,∆)是一个Menger PSM-空间,{xn}是X中的序列,则以下叙述等价:

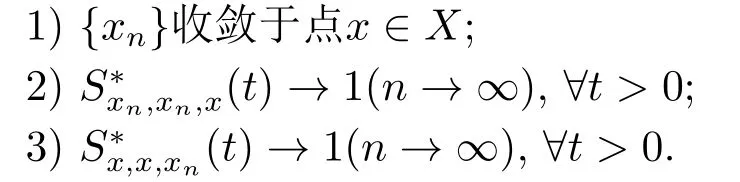
证1)⇒2).

引理2.4设(X,S∗,∆)是一个具有连续t-范数∆的Menger PSM-空间,则以下叙述等价:

1) 序列{xn}是柯西序列;

2) 对任意的ϵ >0,0<δ <1,存在正整数M(ϵ,δ),使得当n,m >M(ϵ,δ)时,1−δ.

证 1)⇒2) 由定义2.8中2)直接可得.

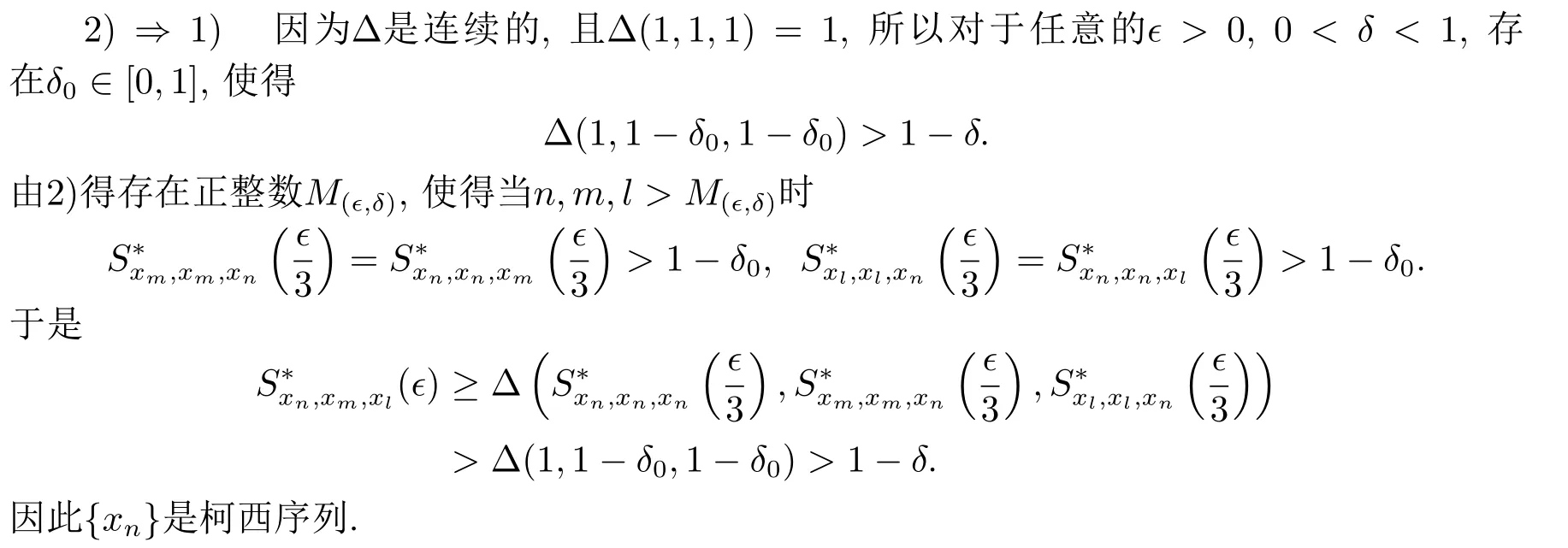
定理2.2设(X,S∗,∆)是一个具有连续t-范数∆的Menger PSM-空间,{xn},{yn}是X中的两个序列,x,y ∈X.如果xn →x,yn →y(n →∞),则对于任意的t >0,.

证对于任意的t>0,存在δ >0,使得t>2δ,则

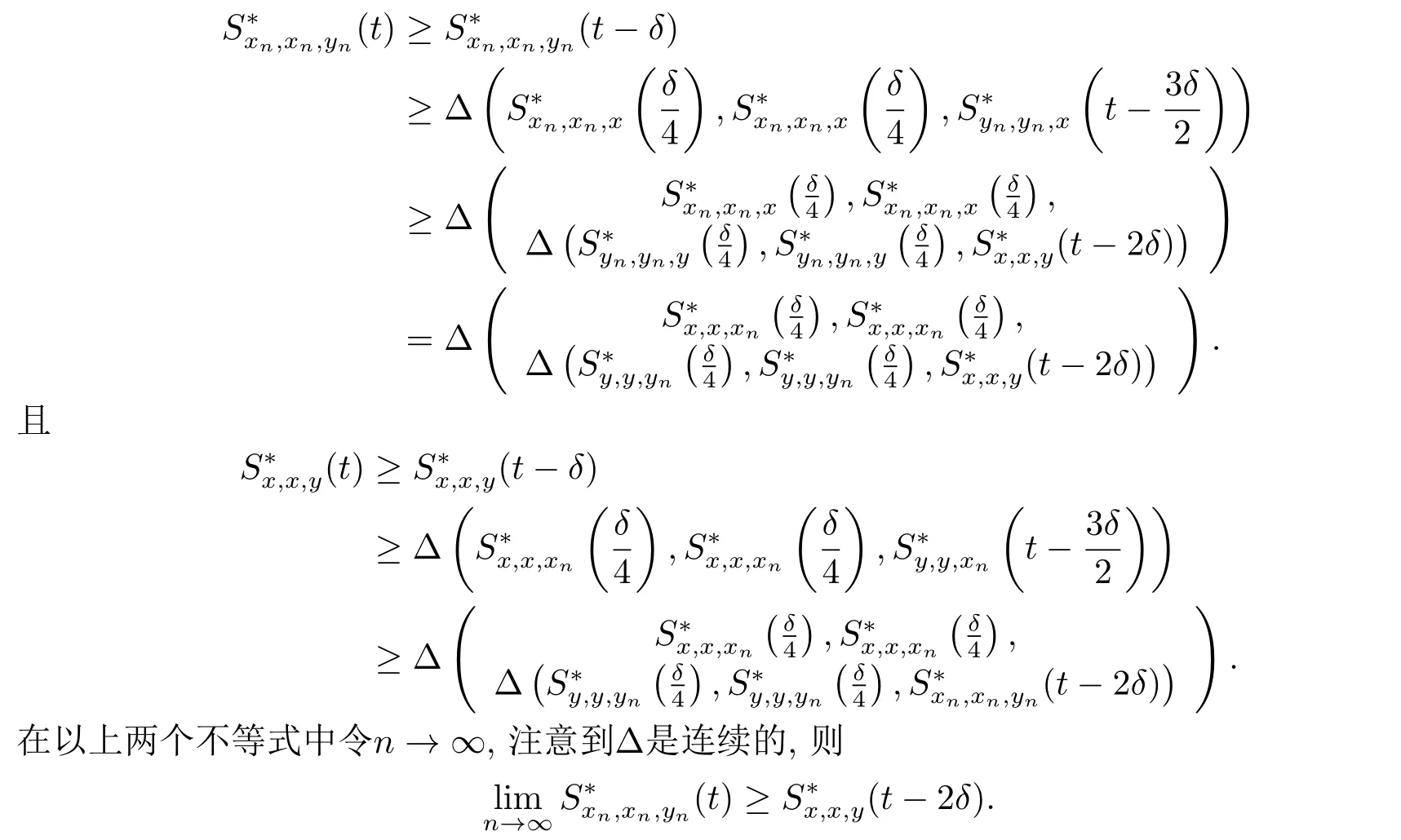
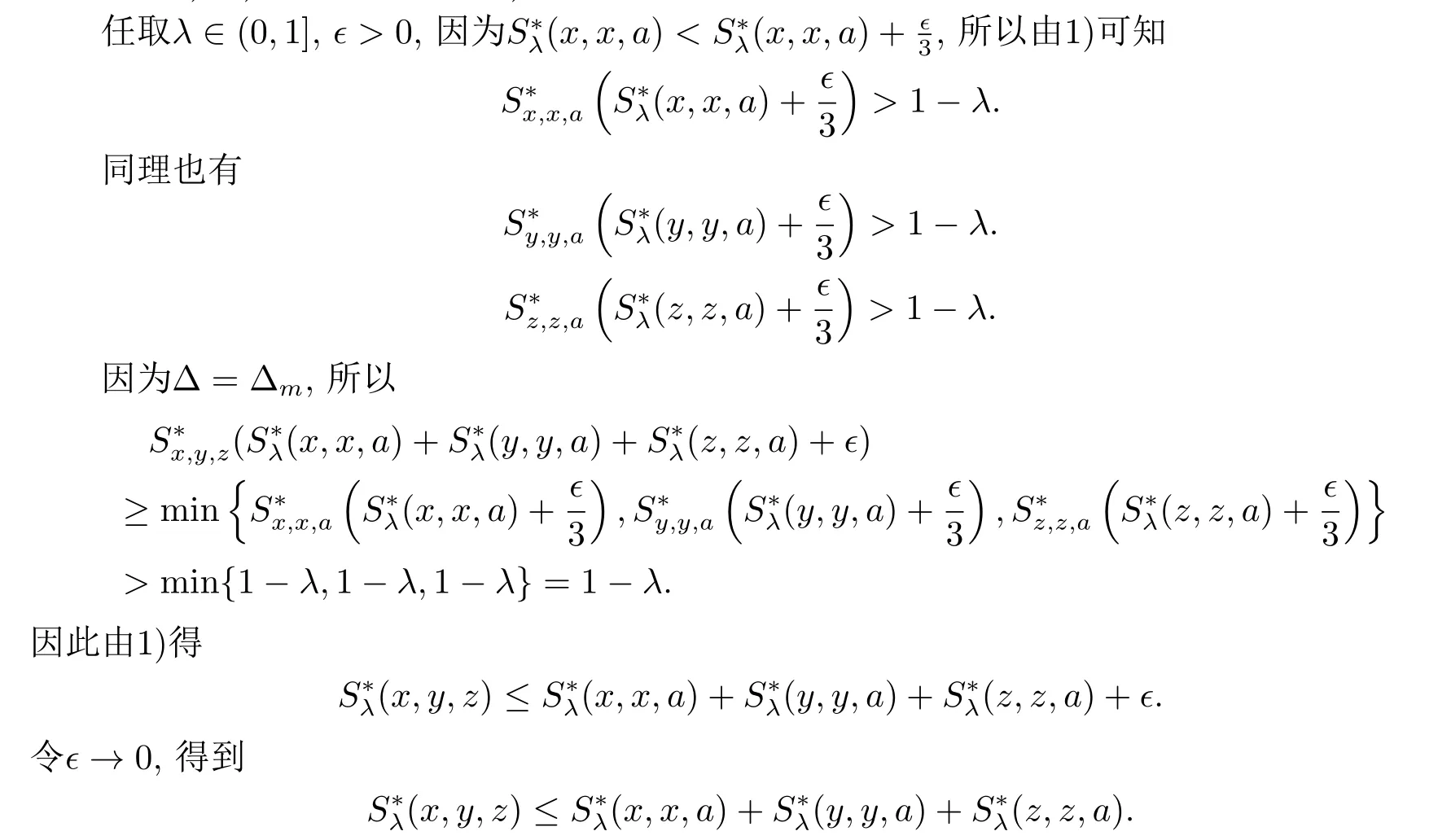
注2.1若映射g是恒等映射,则定义2.11和定义2.13等价.

定义2.14[15]一个元素(x,y)∈X×X被称为是映射G:X×X →X和g:X →X的耦合重合点,如果G(x,y) =g(x),G(y,x) =g(y).称(x,y)是G和g的耦合公共不动点,如果G(x,y)=g(x)=x,G(y,x)=g(y)=y.

定义2.15[15]设X是一个非空集合,G:X×X →X,g:X →X.映射G和g被称为是可交换的,如果对于任意的x,y ∈X,g(G(x,y))=G(g(x),g(y)).

3.主要结果

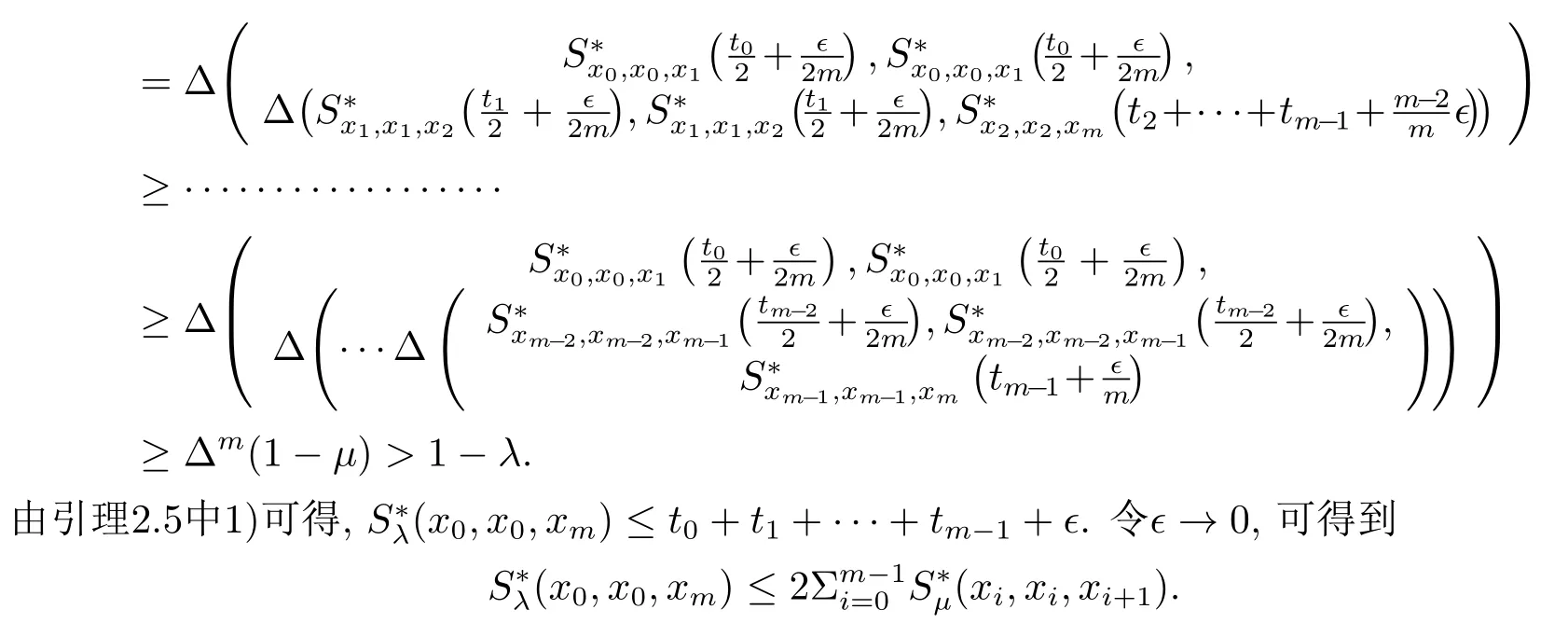
即

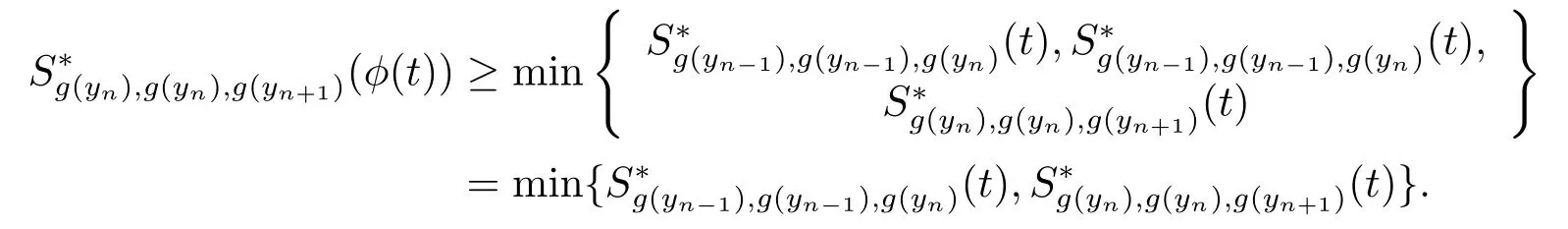
由引理3.2知{g(yn)}也是一个柯西序列.

因为X是完备的,所以存在x,y ∈X,使得

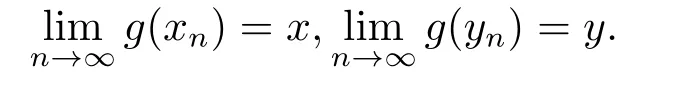
由g的连续性可得

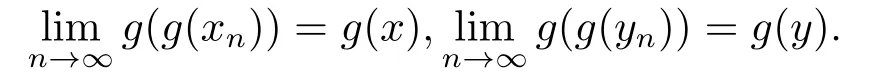
因为G和g是可交换的,所以

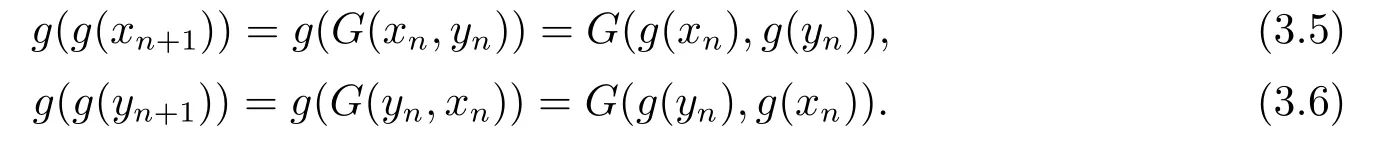
下证g(x)=G(x,y),g(y)=G(y,x).

假设条件(a)满足,在式(3.5),(3.6)中令n →∞,由G的连续性可得

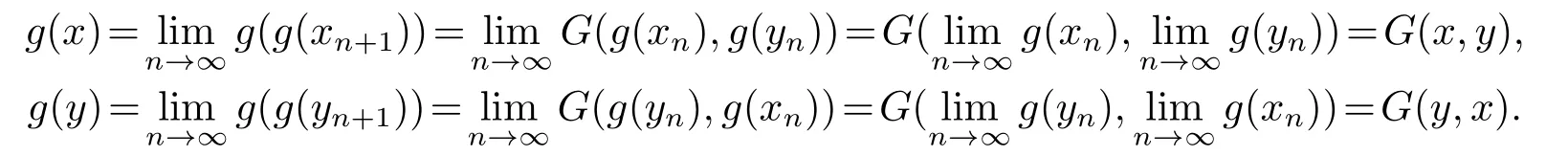
因此,g(x)=G(x,y),g(y)=G(y,x).

假设条件(b)满足,因为{g(xn)}是不减的,{g(yn)}是不增的,并且当n →∞,g(xn)→x,g(yn)→y,所以由条件(b)可知g(xn)≤x,g(yn)≥y,∀n ≥0.则由(PSM-2)和式(3.4)有

同理可得g(y)=G(y,x),因此(x,y)是映射G和g的耦合重合点.

下证讨论耦合公共不动点的存在性和唯一性.注意到如果(X,≤)是一个偏序集合,则可在乘积X×X中定义以下偏序关系:

∀(x,y),(u,v)∈X×X,(x,y)≤(u,v)⇔x ≤u,y ≥v.

定理3.2在定理3.1的条件下,如果对每一个(x,y),(x∗,y∗)∈X×X,都存在(u,v)∈X×X,满足g(u)≤g(v)或者g(v)≤g(u),使得(G(u,v),G(v,u))∈X×X与(G(x,y),G(y,x))和(G(x∗,y∗),G(y∗,x∗))可比较,则G和g有唯一的耦合公共不动点,即存在唯一的(x,y)∈X×X,使得x=g(x)=G(x,y),y=g(y)=G(y,x).

证由定理3.1,耦合重合点构成的集合非空.下证如果(x,y),(x∗,y∗)是映射G和g的两个耦合重合点,即g(x)=G(x,y),g(y)=G(y,x)和g(x∗)=G(x∗,y∗)且g(y∗)=G(y∗,x∗),则必有

g(x)=g(x∗),g(y)=g(y∗).

由假设存在(u,v)∈X×X,使得(G(u,v),G(v,u))∈X×X与(G(x,y),G(y,x))和(G(x∗,y∗),G(y∗,x∗))是可比较的,令u0=u,v0=v,则存在u1,v1∈X,使得g(u1)=G(u0,v0),g(v1)=G(v0,u0).类似于定理3.1的证明,可得到序列{g(un)},{g(vn)},满足

g(un+1)=G(un,vn),g(vn+1)=G(vn,un).

同样地,类似于定理3.1可证明{g(un)},{g(vn)}存在极限.

更进一步,令x0=x,y0=y,x∗0=x∗,y∗0=y∗,同样地,可得到序列{g(xn)},{g(yn)},{g(x∗n)},{g(y∗n)}满足

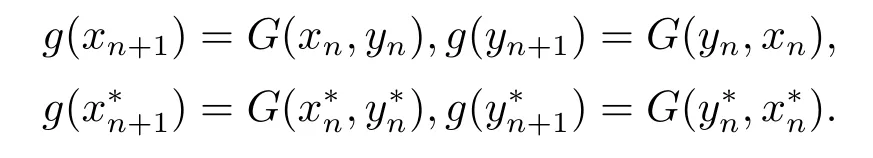
因为

(G(x,y),G(y,x))=(g(x1),g(y1))=(g(x),g(y))

和

(G(u,v),G(v,u))=(g(u1),g(v1))

是可比较的,不妨假设g(x)≤g(u1),g(y)≥g(v1)((g(x)≥g(u1),g(y)≤g(v1)的情况证明类似).容易得到(g(x),g(y))和(g(un),g(vn))是可比较的,即对任意的n ≥1,

g(x)≤g(un),g(y)≥g(vn).

由式(3.4),对于任意的n ≥1有

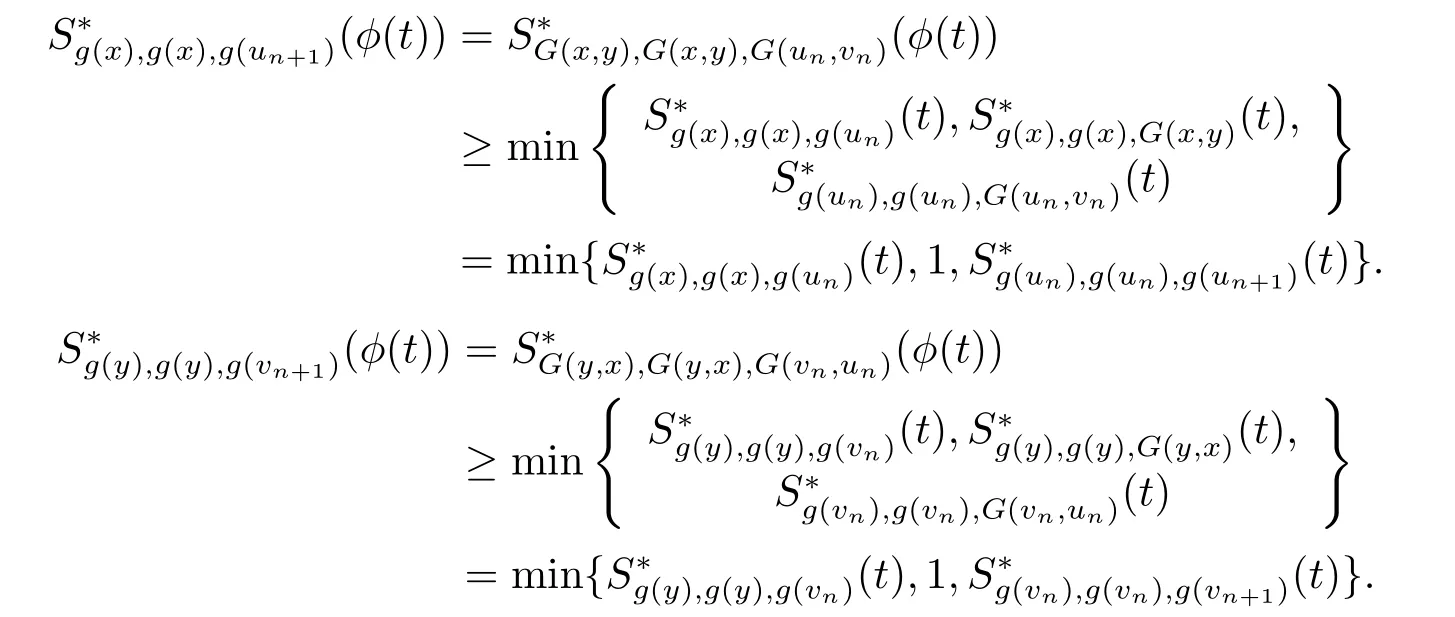
令n →∞,由定理2.2和引理2.6可得

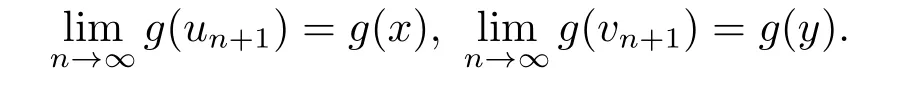
类似地,在定理3.2中令g=I或ϕ(t)=kt,可得相应推论,限于篇幅省略.

4.应用

例4.1设X=[0,1],S(x,y,z)=|x−z|+|y−z|,min{a,b,c},∀a,b,c ∈[0,1],则(X,S∗,∆)是一个完备的Menger PSM-空间.定义g:X →X和G:X×X →X如下: