基于离散观测下Cauchy-OU过程的最大似然估计

陈至芬,陈晓鹏

(汕头大学理学院数学系,广东 汕头515063)

1.引言

随机过程X={X(t),t ≥0}称为Ornstein-Uhlenbeck(OU)型的,如果它满足随机微分方程

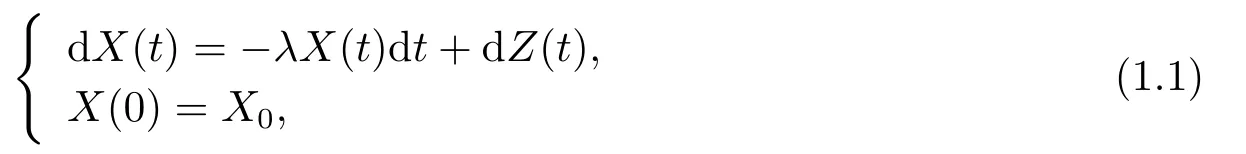
其中Z={Z(t),t ≥0}是一个背景驱动Lévy过程(参考文[1]),强度参数λ >0,初始条件X0与Z无关.参考文[2]证明了Z存在右连左极的修正,本文仅考虑(1.1)式的如下修正过程

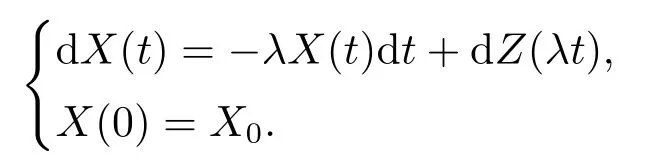
这里修正Z(λt)去除了X(t)在平稳性中对λ的依赖,即无论λ取何值,X(t)的边缘分布都不发生改变.

OU型过程在金融和经济等领域有着十分广泛的应用,例如Barndorff-Nielsen和Shephard[3]提出了利用Gamma-OU和IG-OU等OU型过程来刻画金融资产的波动情况.在本文中,我们主要感兴趣的是研究Cauchy-OU过程的参数估计问题.

但在实际应用中,连续时间的随机微分方程模型总是在离散的时间上观测.到目前为止,基于离散观测的统计方法已经得到了广泛发展,其中最大似然估计法是最常见的一种方法.然而,除了极少数特殊的过程外,OU型过程的似然函数并没有简单的闭型解析式.目前,对于离散时间观测采样,计算似然函数的现有方法包括数值求解Fokker-Planck-Kolmogorov偏微分方程[4]或模拟大量采样路径并沿着这些路径对过程进行精细的采样[5−6].但以上的这些方法并不能够在参数空间上得出能使之最大化的闭型解析式.另外,对于布朗运动驱动的随机微分方程,Aït-Sahalia[7]提出利用Hermite多项式来构造一个显式的闭型函数序列的一种封闭的估计方法.对于Gamma-OU过程,ZHANG[8]等通过特征函数及拉普拉斯逆变换得到转移密度函数,再利用Gaver-Stehfest算法构造了似然函数的逼近序列,最后得到Gamma-OU过程的最大似然估计.

受以上所述文献启发,本文采用Gamma-OU过程参数估计的研究思路,主要研究了离散观测样本下,以复合泊松过程为背景驱动的Ornstein-Uhlenbeck过程的最大似然估计.我们假定离散时间观测Xk=X(tk),其中{tk=k∆,k=0,1,··· ,n},∆>0固定,考虑强度参数和密度参数的估计.

本文其他部分安排如下: 第2节介绍了Cauchy-OU过程.第3节推导出Cauchy-OU过程的累积分布及转移密度函数.第4节构造了转移密度函数的近似序列.第5节讨论未知参数的估计及其仿真.第6节得出结论及后续工作.

2.Cauchy-OU过程

随机过程X={X(t),t ≥0}称为Cauchy-OU过程,如果满足下列齐次线性随机微分方程

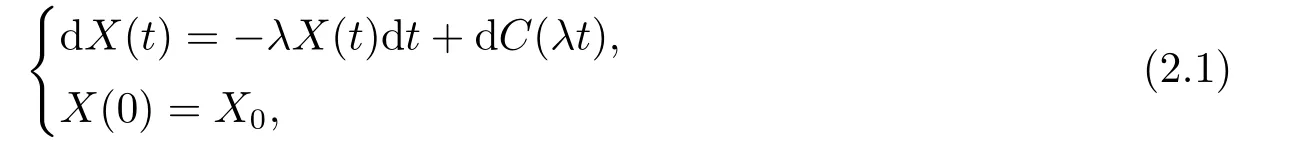
其中{C(t),t ≥0}具有正增量,是一个背景驱动Lévy过程,强度参数λ >0,且不论λ取何值,X(t)的边缘分布都是Cauchy分布.

根据Lévy过程的相关积分理论[9],易证得(2.1)式存在如下强解

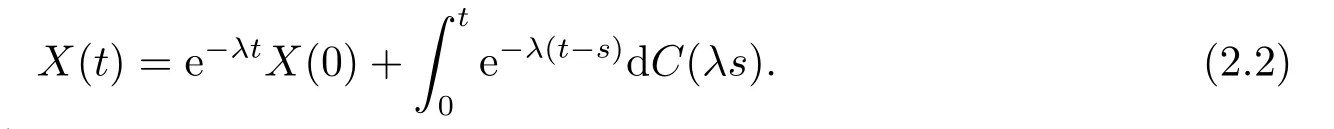
对于任一∆>0,递归地有

命题2.1假设ϕ(u)为分布的特征函数,则其累积特征函数(也称特征指数)ψ(u) =logϕ(u)满足如下Lévy-Khinchine公式

命题2.2对任意固定的λ>0,若X是由(σ,γ,ν,λ)生成的OU型过程,并且Lévy测度ν满足

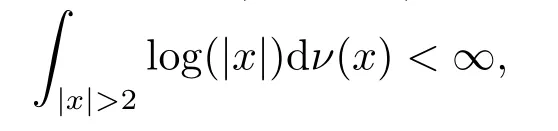
根据Acceptance-Rejection算法,取定λ=1,a=0.5,∆=0.5,n=100,利用MATLAB模拟以上复合泊松过程(参考文[12]),得到如下图2.1以C(λt)过程为例的一个仿真路径.

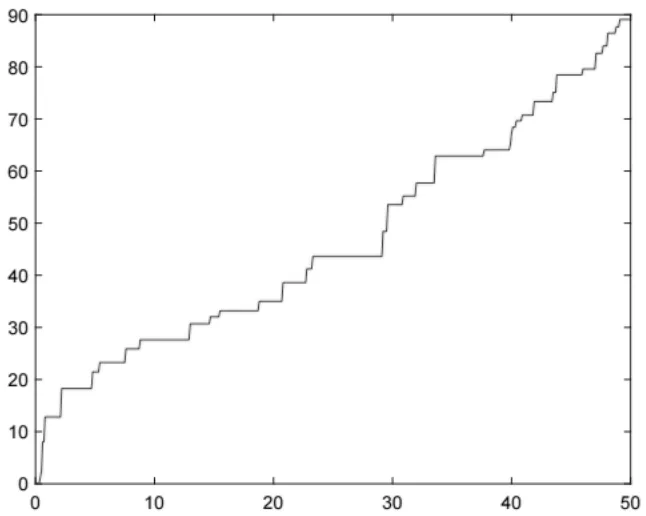
图2.1 复合泊松过程C(λt)关于t 的图像(λ=1, a=0.5,∆=0.5, n=100)

由(2.2)式易知X(t)是左极右连半鞅[2],故OU过程{X(t),t ≥0}可假定为左极右连的.又因为在概率意义上,C(t)的路径在每个区间(0,t],t ∈(0,∞)上是有限变差函数(almost-surely),故(2.2)式可看作是一个Lebesgue-Stieltjes积分.

记

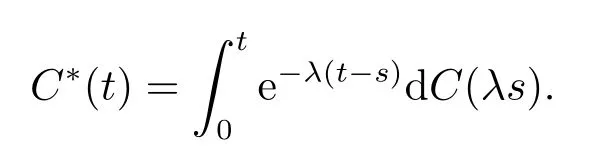
并且根据文[2]中的引理17.1可知,

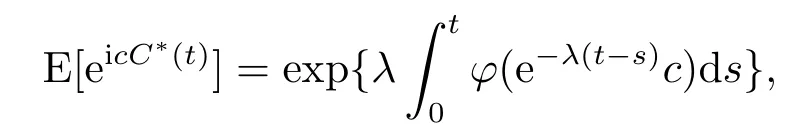
其中

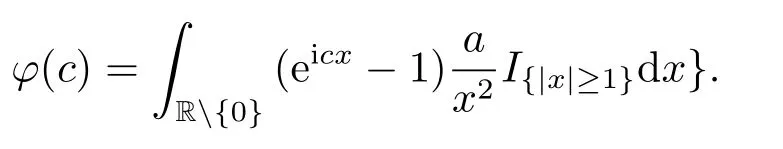
于是,

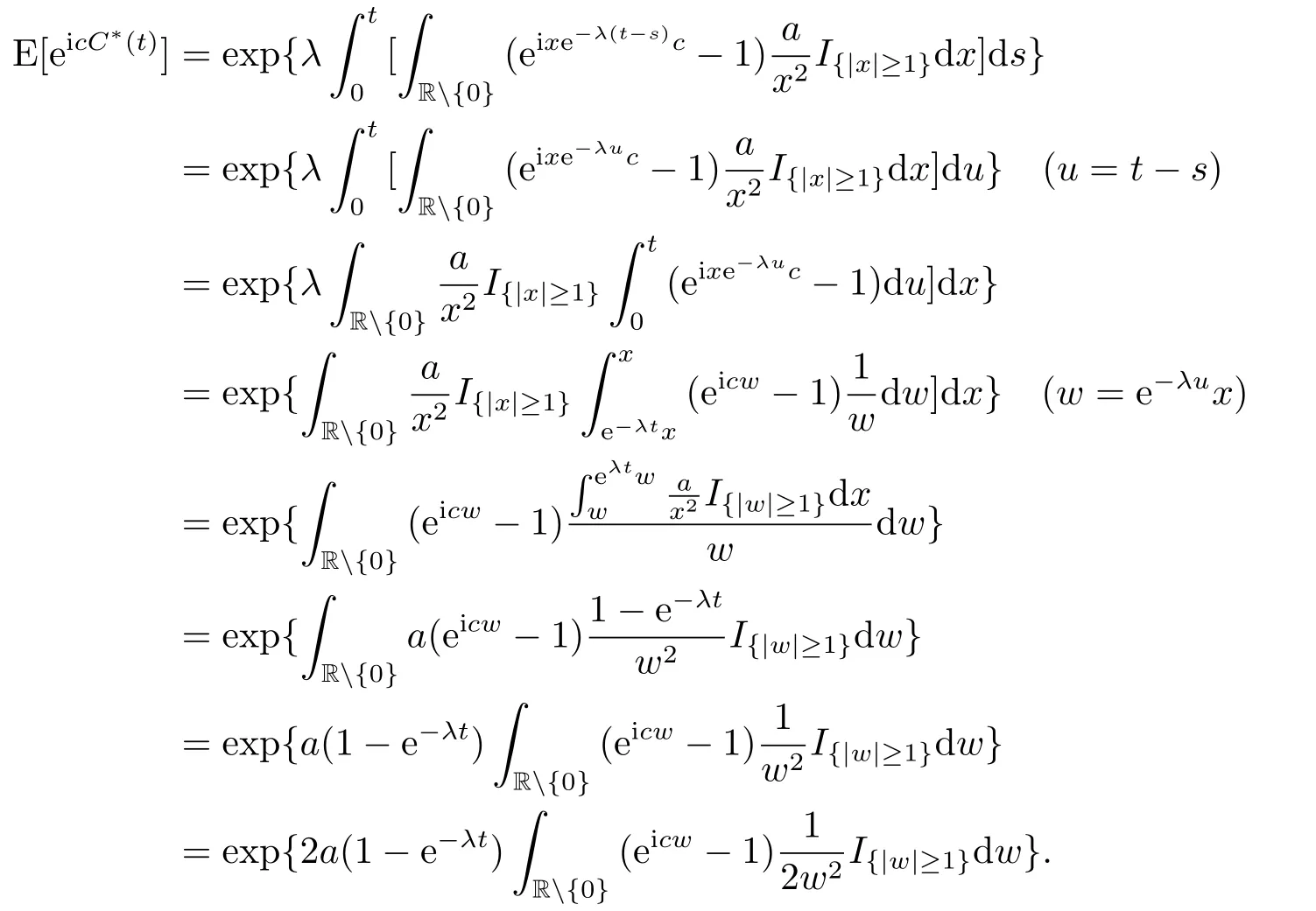
所以,{C∗(t),t>0}是一个复合泊松过程,即

3.Cauchy-OU过程的转移密度推导

为了得到Cauchy-OU过程{X(t),t ≥0}的转移概率密度,先考虑其累积分布函数.

引理3.1对固定t>0,C∗(t)的累积分布函数为

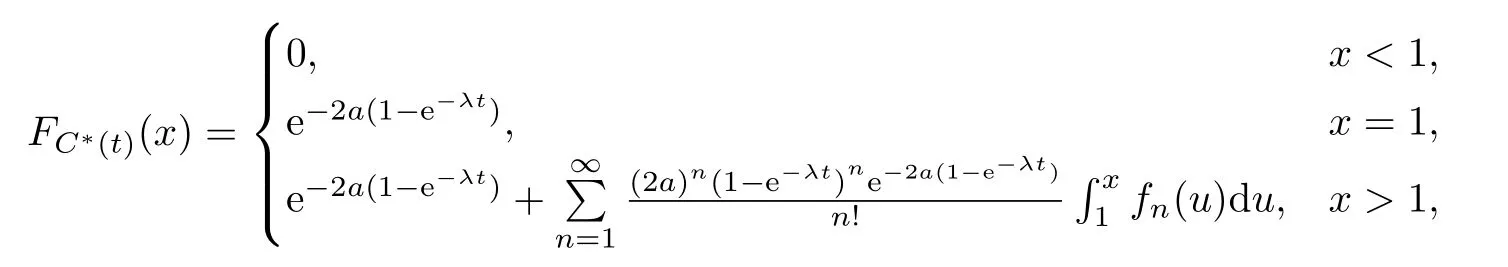
其中,对于fn(x)(n ≥1),这里定义为f1(x)=f(x),

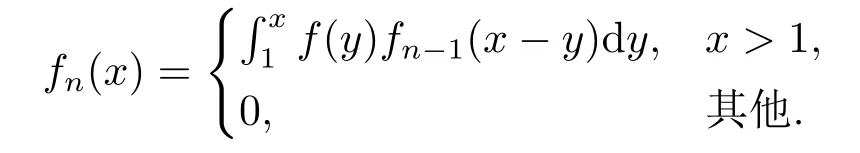
证考虑到(2.4)式中W1,W2,···是一列独立同分布的正随机变量序列,且其密度函数为(2.5)式,故当x ≤1时,引理3.1成立;对x>1时,C∗(t)的累积分布函数为

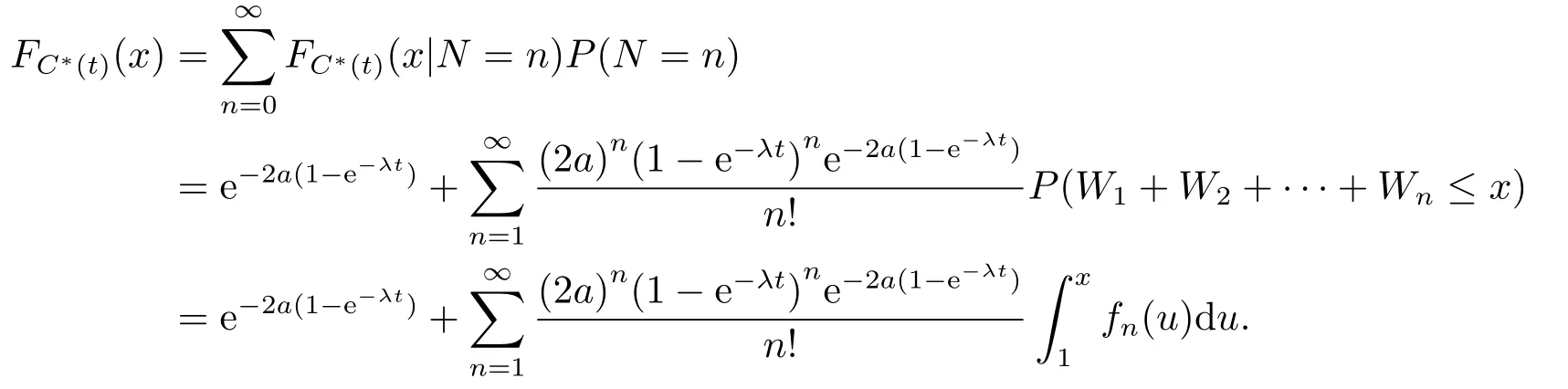
引理3.2对固定t>0,随机变量C∗(t)的密度函数可以表示为

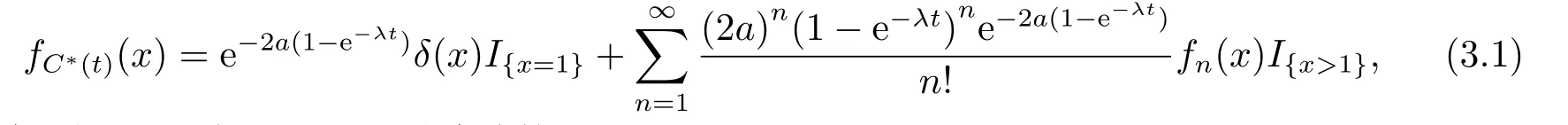
其中,当x>1时,fC∗(t)(x)是连续的.

证我们分以下步骤讨论:

(i) 当x>1时,(2.5)式中定义的f(x)单调递减;

(ii) 对∀n>0及x>1,有

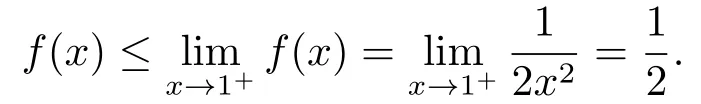
所以,

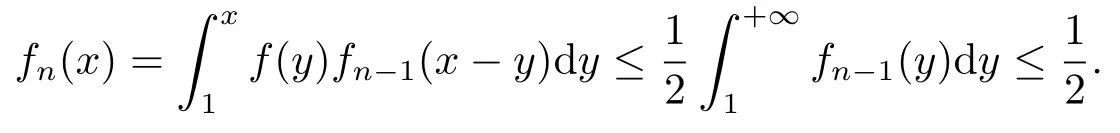
(iii) 因为

定理3.1(2.2)式中Cauchy-OU过程X(t)的时间齐次转移函数为

其中p(t,y;x,λ,a)表示X(t)在时间区间(0,t]上从x到y的转移函数.

4.转移密度函数的近似

为了得到转移密度p(t,y;x,λ,a)的估计,固定t,y,x,λ和a,令

5.未知参数的估计与仿真

先观察强度参数λ和密度参数a分别对Cauchy-OU过程X(t)的影响,不妨取定∆= 0.5,样本容量n=100.下面图5.1-5.3是a=0.5,λ分别取值为λ=0.1,λ=1和λ=10时X(λt)关于t的变化情况.而图5.4-5.6是λ=1,a分别取a=0.1,a=0.5 和a=1 时X(λt)关于t的变化情况.

总体上,强度参数λ值的不同,对其波动即Cauchy-OU过程X(λt)的影响比较大,且由以上述图5.1-5.3可以观察到强度参数λ值越大,该过程的波动频率越大;而图5.4-5.6可以看到相对强度参数λ而言,密度参数a对模型的波动影响较小一些.故此,下文优先选择对强度参数λ进行估计.

Ⅰ强度参数λ的估计

假定在离散时间观测下,令Xk=X(tk) =X(k∆),其中{tk=k∆,k=0,1,··· ,n},∆>0固定.令(X0,X1,...,Xn) 的一个样本值为(x0,x1,...,xn),则由定理3.1及贝叶斯法则知似然函数具有如下形式

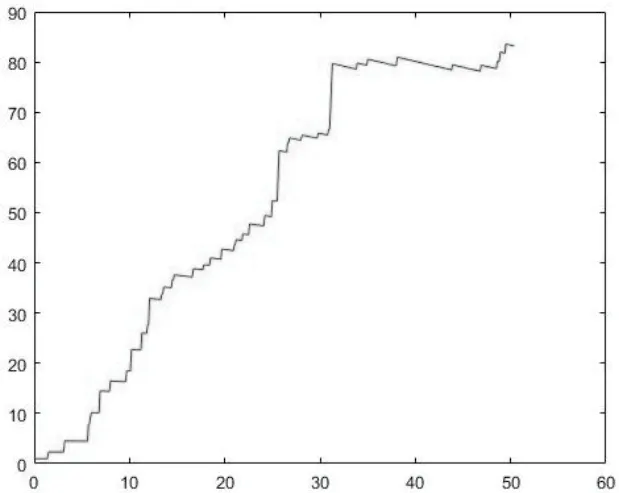
图5.1 X(λt)关于t 的图像(λ=0.1, a=0.5,∆=0.5, n=100)

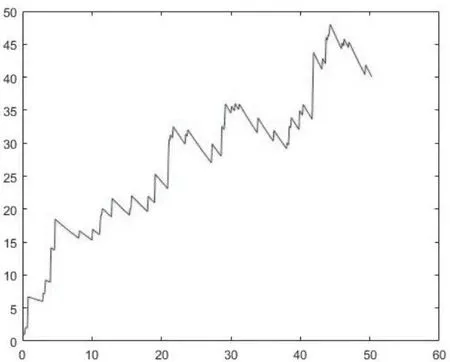
图5.2 X(λt)关于t 的图像(λ=1, a=0.5,∆=0.5,n=100)

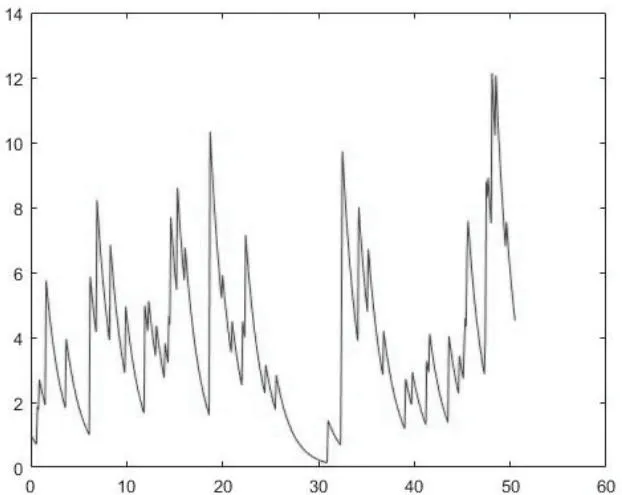
图5.3 X(λt)关于t 的图像(λ=10, a=0.5,∆=0.5, n=100)

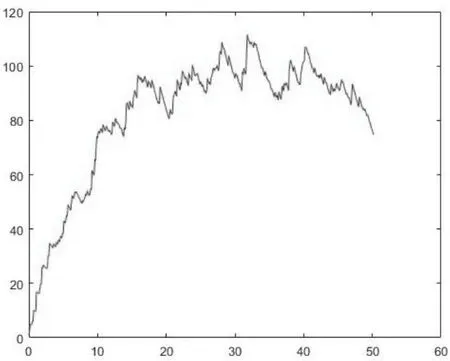
图5.4 X(λt)关于t 的图像(a=0.1, λ=1,∆=0.5,n=100)

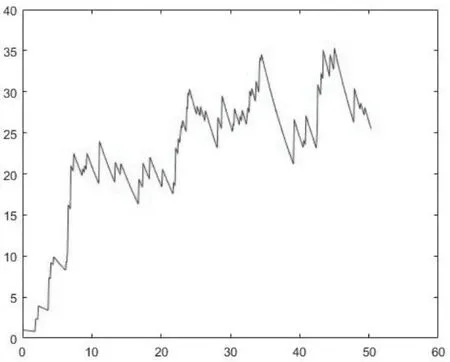
图5.5 X(λt)关于t 的图像(a=0.5, λ=1,∆=0.5, n=100)

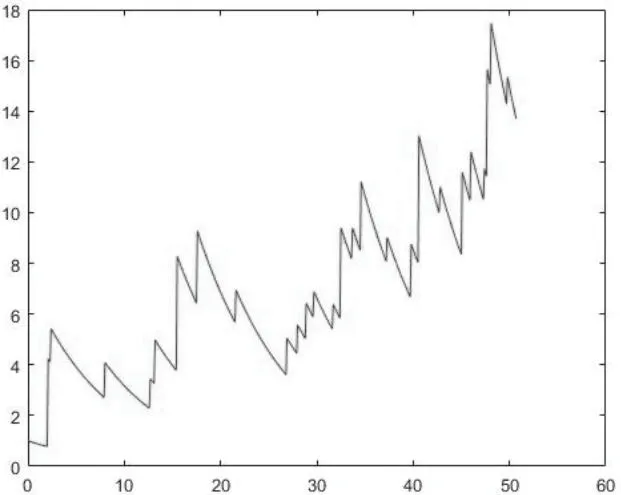
图5.6 X(λt)关于t 的图像(a=1, λ=1,∆=0.5,n=100)

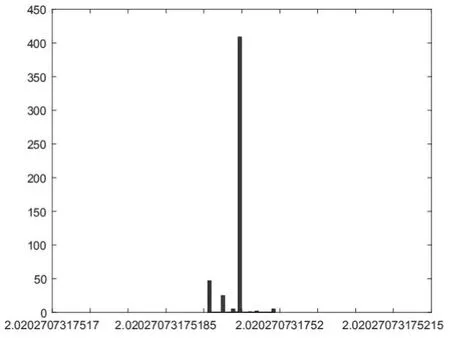
图5.7 估计值n的直方图(真实值λ=2, a=0.5,∆=1, n=100)

为了得到强度参数λ更加精确的估计,分别取样本容量n=100,n=200和n=400进行试验,假定∆=1,a=0.5,通过仿真得到估计值的均值,方差以及误差如下表.

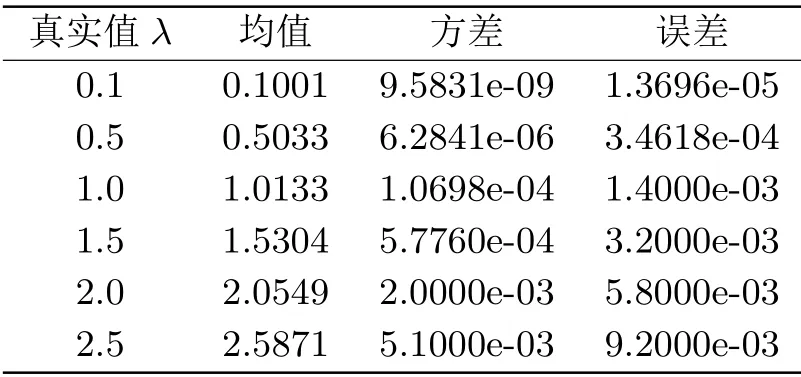
表5.1 样本容量n=100下关于强度参数λ的估计表

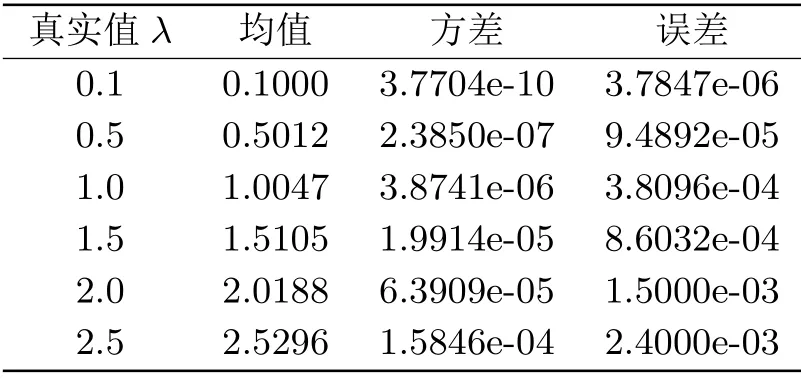
表5.2 样本容量n=200下关于强度参数λ的估计表

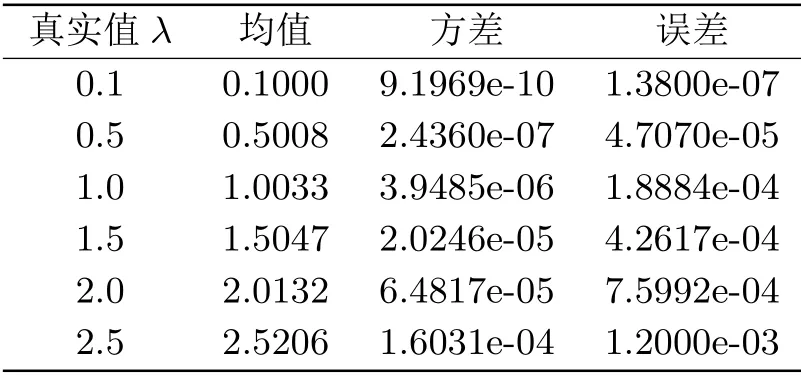
表5.3 样本容量n=400下关于强度参数λ的估计表

由上述表5.1-5.3可见,随着样本容量n的增加,所得到估计值ˆλn的误差逐渐减小,即估计更加准确.另外,由以上表中可以发现,当真实值λ取值为0.1时,所得到估计的误差最小,故以下文章将假定强度参数λ的估计值为0.1来进行对密度参数a的估计.

Ⅲ密度参数a的估计

通过上面方法已经得到参数λ的估计值,不妨记为λ0.接下来估计密度参数a.我们假定强度参数λ是已知的,即令λ=λ0.此时,(5.1)式即为

Ⅳ密度参数a的仿真

由5.1节我们已经得到了强度参数λ的真实估计值λ0,通过5.2节得出了密度参数a的估计方法.这里,我们同样取定∆=1及已估计值λ=λ0=0.1(假定取为0.1).利用MATLAB仿真,这里我们分别取样本容量n=200和n=400进行试验,假定∆= 1,λ=0.1,通过仿真得到估计值ˆan的均值,方差以及误差如下表.

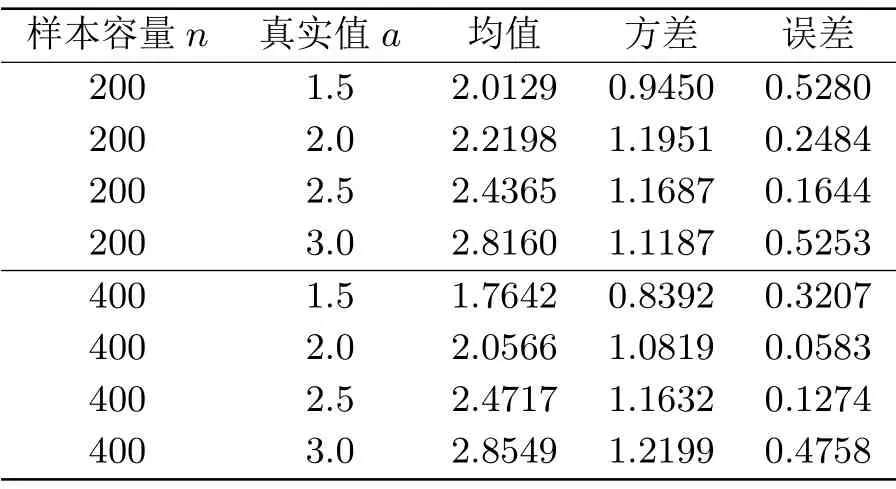
表5.4 不同样本容量n下关于密度参数a的估计表

6.结语

本文在离散观测样本下通过转移函数,采用最大似然估计法研究了Cauchy-OU过程的参数估计问题.通过傅里叶变换及Gaver-Stehfest算法,构造了收敛于真实但未知的似然函数的一个显式逼近序列,从而建立了基于离散时间下Cauchy-OU过程X(t)的似然函数.通过实验仿真,发现强度参数λ对该过程的波动影响明显大于密度参数a的影响,故此优先估计出强度参数λ,再根据最大似然估计法得出密度参数a的估计值.最后的仿真结果表明,本文得到的强度参数和密度参数估计是比较准确且稳定的.在后续工作中,可以考虑其他更一般的OU类过程的参数估计问题,这将在金融领域中对分析资产波动具有重要的作用,但其相应的最大似然函数的解析表达式将会是一个继续深入研究的问题.