污染环境中具有尺度结构的周期种群系统的最优控制

龚薇,王战平

(宁夏大学数学统计学院,宁夏 银川750021)

1.引言

随着环境污染日益严重,种群的生存面临着极大威胁.因此,我们需要建立模型去解决污染环境中的问题.然而,大量的生态学研究表明,个体尺度结构差异要比年龄结构对种群的发展具有更为重要的影响.鉴于种群的生存环境经常会经历如季节影响等周期性变化,这样的外部环境对资源开发具有很大的影响.由此,研究污染环境中具有个体尺度周期种群系统的最优控制问题就有了非常重要的现实意义.

近些年,关于年龄结构的种群模型的行为分析和控制问题有大量的研究成果.1998年,Anita等研究了周期环境中线性种群模型的最优收获问题,主要关注收获总量[1],接着又研究了与年龄相关的种群动力系统的最优收获[2].2002年,陈仁昭等人[3]研究具有空间扩散的种群系统解的存在唯一性及边界控制.2005年,付军等人[4]研究了年龄相关的种群空间扩散系统的广义解及收获控制.同年,雒志学和王绵森[5]研究了一类具有年龄结构的线性周期种群动力系统的最优收获控制问题,主要关注总的经济效益.2006年,何泽荣[6]研究了具有年龄结构竞争种群的最优收获.Hritonenko,Yatsenko[7]研究了一类非线性森林资源模型的最优开发问题,利用变分法推出了最优性条件.2010年,何泽荣[8]又研究了具有年龄结构和约束的群落系统的最优收获.同年,孙宏雨和赵春[9]研究了具有年龄结构两竞争种群系统的适定性和最优控制.与此同时,大量的学者又将个体尺度作为研究的重点,Eucario等人[10]研究了一类具有尺度结构资源模型的最优收获问题.2008年,Kato研究了非周期环境具有尺度结构线性种群系统的最优控制[11],随后,又研究了非线性种群系统的最优控制问题[12].Gasca-Leya和Hernandez[13]讨论了一类线性尺度结构模型的最优收获时间,并与非结构化模型做了对比.何泽荣等人研究了一类周期环境中具有尺度结构的种群模型的适定性及最优收获问题[14],接着又提出了模拟周期环境和尺度结构的种群系统的最优收获率问题[15].2019年,梁丽宇和雒志学[16]研究了周期环境中具有尺度结构的捕食种群系统的最优控制问题.目前,考虑个体尺度的种群模型较多,但在污染环境中具有个体尺度周期种群系统的最优控制种群模型尚且没有,而这样建立的模型更符合实际.

本文结构如下: 第二节提出基本模型,第三节讨论解的存在唯一性,第四节用极大值原理及紧性讨论控制问题的存在性,最后利用法锥技巧得到控制问题的最优条件.

2.基本模型

本文提出并研究如下污染环境中具有尺度结构周期种群系统模型：

本文做以下假设:

3.状态系统的适定性

在本节中,不失一般性,假设α(x,c0(t),J(t))≡0,模型(2.1)变为如下形式:

定义1φ(t;t0,x0)为初始条件x(t0) =x0下常微分方程x′(t) =V(x,t)的解,称其为系统(2.1)通过点(t0,x0)的特征曲线.特别地,在x−t平面上,记通过点(0,0)的特征曲线为z(t).

引理1若函数u(x,t)∈L∞(Q),沿着每条特征曲线φ都绝对连续,且满足

则称(u(x,t),c0(t),ce(t))为系统(3.1)的解.这里Dφu(x,t)表示u(x,t)沿特征曲线φ的方向导数,即

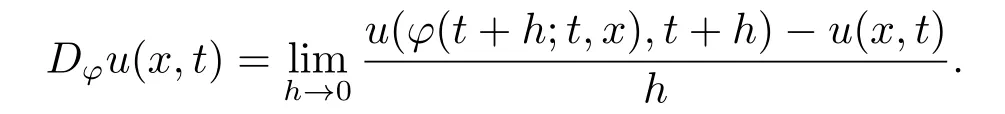
证对于x−t平面上第一象限任意固定(x,t),当x ≤z(t),定义初始时刻τ=τ(x,t)使得φ(t;τ,0)=x.于是有φ(t;τ,x)=0.对于固定函数从而利用特征线法可知,当x ≤z(t)时有

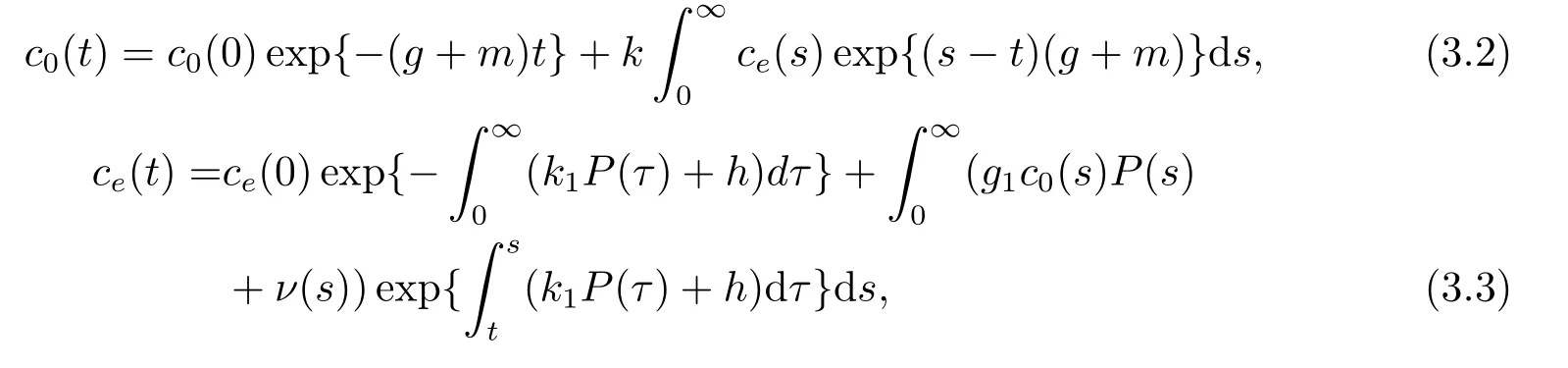
引理2存在正的常数F1,F2,B1,B2,使得对任意J1,J2,R1,R2∈H,t ∈(0,T),有

4.最优策略的存在性

本节我们考虑下述周期环境中的最优收获问题:

其中ω(x,t)≥0为权函数,表示t时刻尺度为x的个体的经济价值.记uα(x,t)为给定α ∈Ω时控制系统(2.1)的解,因此J(α)表示在种群演变的一个周期内人类开发资源所获得的总经济效益.

定理4控制问题(2.1),(4.1)至少存在一个最优解.

证令由定理3中3)可知,

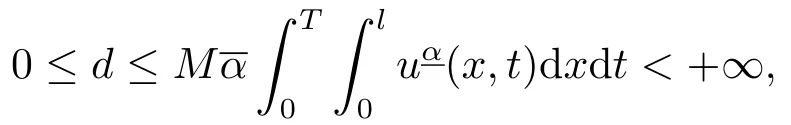
其中M为权函数ω(x,t)的上界.

另一方面

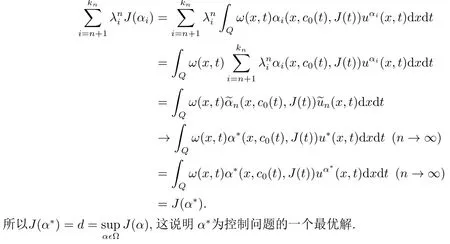
5.最优策略的结构

其中

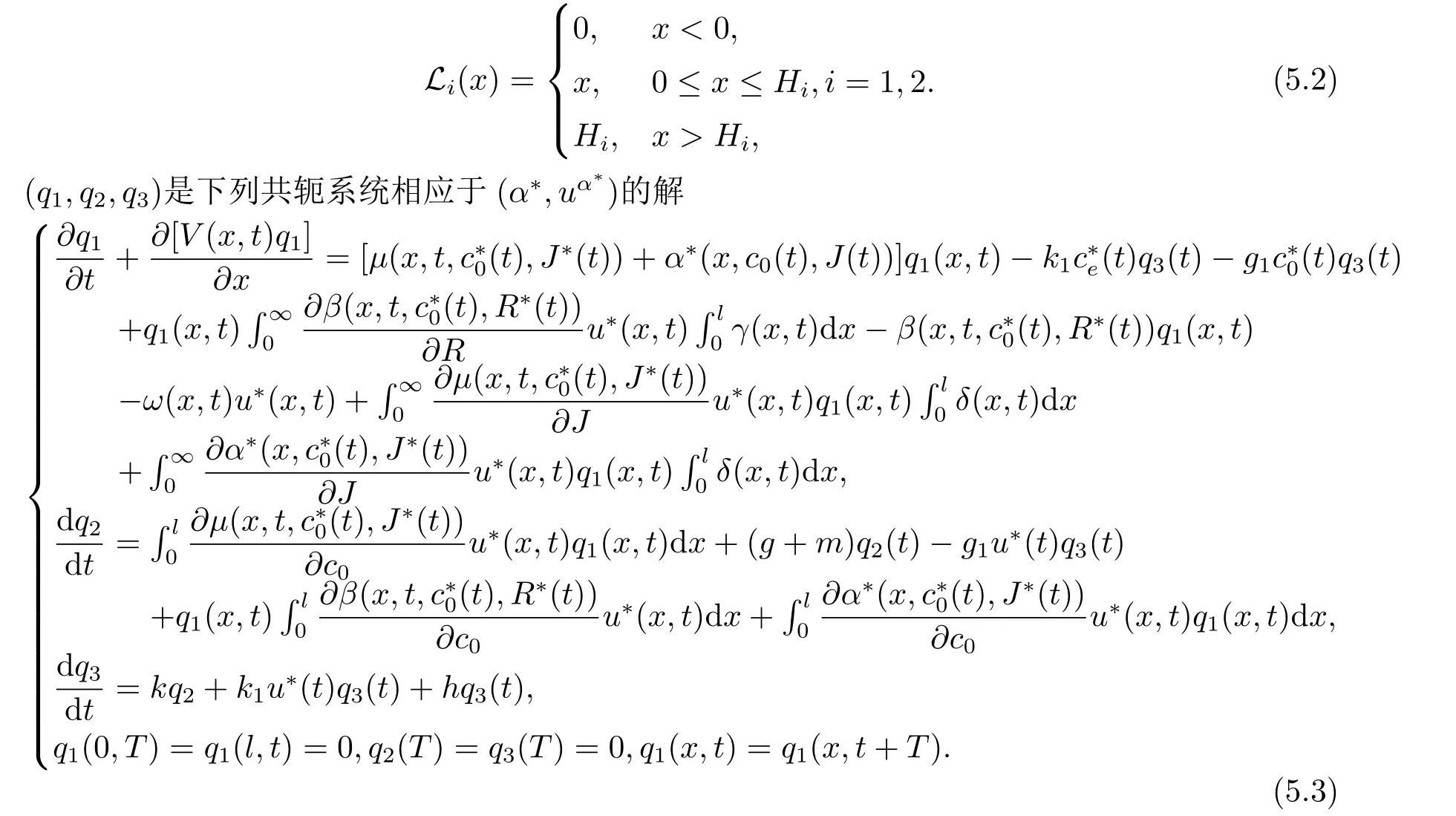
证因为是控制问题(2.1)的最优对,对于任意固定的ν ∈TΩ(α∗),以及充分小的ε>0时,有αε:=α∗+εν ∈Ω,由J(α∗)为J(α)的最大值,即J(u∗+ε,v∗+ε)≤J(u∗,v∗),

可得

在(5.5)的前三式分别乘以q1,q2,q3,第一式在Q上积分,第二,第三式在上积分得以下结果:

在(5.5)的一式两边同时乘以q1,并在Q上积分,得