带约束集值均衡问题的近似Henig有效解

胡莎莎,徐义红,牛智超

(南昌大学数学系,江西 南昌330031)

1.引言

向量均衡问题是许多实际领域中的一个广泛问题.它涵盖了许多典型的数学问题,如向量优化,变分不等式,向量纳什均衡,向量互补等.它广泛应用于投资决策,定量经济,最优控制和工程技术.由于所涉问题的普遍性和统一性以及解决这些问题之普遍,向量均衡问题已成为运筹学和非线性分析领域的热点问题[1−6].LONG等[1]在近似锥次类凸性假设下获得了带函数约束的向量均衡问题Henig有效解的最优性条件.Luu等[2−3]建立了带等式和不等式约束的向量均衡问题有效解的充分和必要条件,同时建立了带约束向量均衡问题局部有效解的Fritz-John和Karush-Kuhn-Tucker最优性必要条件.GONG[4−6]在锥凸性假设下获得了带约束向量均衡问题有效解的最优性条件,在Banach空间中利用非线性泛函和Ioffe次可微获得了非凸向量均衡问题弱有效解,Henig有效解,超有效解以及全局有效解的最优性条件.

Gerth等[7]利用非凸分离定理,得到了弱有效点和真有效点的标量化结果.借助Gerstewitz函数,LI等[8]建立了集值非凸优化问题的必要和充分最优性条件.在没有任何凸性假设下,ZHENG[9]利用连续单调Minkowski泛函,获得了赋范空间中Henig有效点的标量化特征.

另外,在非紧可行集的情况下,精确解集有可能是空集,而在条件较弱情况下,近似解集可以是非空的.因此,研究近似解不仅具有理论价值,而且具有实际意义.QIU等[10−11]利用集值函数研究了向量优化问题的近似解,同时得到了向量均衡问题近似弱有效解和近似Henig有效解的标量化特征.

受以上研究的启发,我们在没有任何凸性假设的情况下,利用非线性泛函讨论近似Henig有效解的必要和充分最优性条件.

2.预备知识

由文[7],我们得到泛函ξ的性质.

引理2.1若k ∈intC×intD,(y0,z0)∈Y×Z,则

(i)ξ(y,z)

(ii)ξ(y,z)≤t ⇐⇒(y,z)∈tk+(y0,z0)−cl(C×D);

(iii)ξ(y,z)≥t ⇐⇒(y,z)∉tk+(y0,z0)−intC×intD;

(iv)ξ(y,z)>t ⇐⇒(y,z)∉tk+(y0,z0)−cl(C×D);

(v)ξ(y,z)=t ⇐⇒(y,z)∈tk+(y0,z0)−∂C×∂D;

(vi)ξ是Y×Z上的严格C×D-单调连续凸泛函.

引理2.2若k ∈intC×intD,(y0,z0)∈Y×Z,则对任意的y ∈Y,z ∈Z,α ≥0有

ξ((y,z)−αk)=ξ(y,z)−α.

证对任意的y ∈Y,z ∈Z有

由引理2.2可得下面的推论.

推论2.1若k ∈intC×intD,(y0,z0)∈Y×Z,则对任意的y ∈Y,z ∈Z,下面结论成立

(i)ξ((y,z)+αk)=ξ(y,z)+α,∀α ≥0;

(ii)ξ((y,z)−αk)<ξ(y,z)<ξ((y,z)+αk),∀α>0;

(iii)ξ((y,z)+α1k)<ξ((y,z)+α2k),∀α1<α2.

3.带约束集值均衡问题的最优性条件

下证ψ(−ε,0)≥0.若t<0,则t(b0,d0)∈−intcone(B+U)×intD.由cone(B+U),D是点锥得(cone(B+U)×D)∩(−(intcone(B+U)×intD))=∅,于是t(b0,d0)∉cone(B+U)×D.因此,若t(b0,d0)∈cone(B+U)×D,则t ≥0.于是由(3.7)得ψ(−ε,0)≥0.

推论3.1设若是(Φ-SEPC)的一个Henig有效解,则存在Y×Z上正齐次次可加连续泛函ψ使得

证由D是凸锥得

推论3.2设B是C的基,¯x ∈A.若存在Y×Z上正齐次次可加连续泛函ψ满足

证由泛函ψ在Y×Z上的正齐次次可加连续性得ψ(0,0)=0.在定理3.2中令ε=0可以证得推论3.2成立.

在定理3.2中,泛函ψ在Y×Z上是正齐次次可加连续的.接下来,我们将减弱泛函ψ在Y×Z上的性质得到下述定理.

定理3.3设ε ∈C,B是C的基,若存在Y×Z上泛函ψ满足

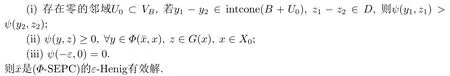
证取一个零的均衡凸邻域U2使得U2⊂VB.令U=U0∩U2,由(i)和(iii)得

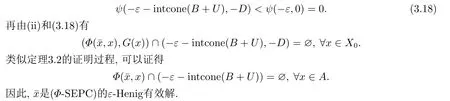
推论3.3设B是C的基,¯x ∈A.若存在Y×Z上泛函ψ满足

(i) 存在零的邻域U0⊂VB,若y1−y2∈intcone(B+U0),z1−z2∈D,则ψ(y1,z1)>ψ(y2,z2);

(ii)ψ(y,z)≥0,∀y ∈Φ(¯x,x),z ∈G(x),x ∈X0;

(iii)ψ(0,0)=0.

证在定理3.3中令ε=0可直接证得推论3.3成立.

4.结论

本文中,我们引进了带约束集值均衡问题近似Henig有效解的概念.在没有任何凸性假设下,利用非线性泛函建立了该解的必要和充分最优性条件(见定理3.1和3.2),且该解的必要和充分条件在形式上大致统一,但在充分条件中要求泛函ψ在Y×Z上是正齐次次可加连续的,条件较强.于是,我们减弱泛函的性质建立了该解的另一充分最优性条件(见定理3.3).最后,我们在上述基础上建立了带约束集值均衡问题Henig有效解最优性条件.