基于博弈论赋权对银行经营绩效的动态评价

王彦伟

(安徽大学 安徽 合肥 230000)

一、理论介绍

(一)改进后的层次分析法(AHP)

一般的层次分析法具有很大的缺陷是当在变量很多的情况下，层次分析法判断矩阵难以得到保证，需进行多次的一致性检验，导致计算量巨大，而且在用整数和倒数表示指标的重要性也难以做到完全客观和准确，因此我们采用3标度的方法对传统的层次分析法进行改进，能够有效地避免决策者的主观意愿带来的误差，提高准确性。

1.建立比较矩阵

我们对一般的层次分析法中的对所有指标进行比较后进行打分进行改进，对俩个变量进行比较，用3标度方法建立比较矩阵：

2.计算重要性排序指数

3.构造新的判断矩阵B

B=(bij)n×n

4.传递矩阵：M=(mij)n×n，mij=lgbij

6.拟优一致矩阵：R=(rij)n×n，rij=10dij

7.计算权重：求R的最大特征根所对应的的特征向量，进行归一化处理，即为权重ω。

(二)改进后的熵值法(EVM)

1.判断矩阵

假设我们收集到n个样本，观察每样本的m维，得到样本数据集X=(xij)n×m，针对各指标的量纲不同，利用下试对数据进行归一化处理

则判断矩阵为：

D=(dij)n×m,(i=1,2,…,n;j=1,2,…,m)

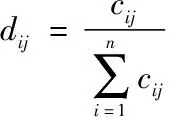
2.计算指标的熵值

传统的求熵方法得到熵值为：

3.各指标权重向量W

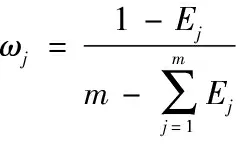
(三)组合赋权-博弈论组合赋权

本文采用综合赋权的方法，基于层次分析法和熵权法，利用博弈论思想，进行综合赋权，以科学的比例分配来平衡各个单一方法对综合权重的作用。

假定采用了K种单一的赋权方法，记为ωi=(ωi1,ωi2,…,ωim),i=1,2,…,k，其中m表示选取的指标个数，则K种权重向量的线性组合可表示为：

根据博弈论的思想，即可以转化为对单一权重向量的线性组合的优化，优化的目标为使得组合权重向量ω与各个单一权重向量的偏差达到最小，可用下式表达：

(四)时序加权平均算子(TOWA)

在动态综合评价问题中，常采用时序加权平均算子对观察年份进行赋权，最终形成指标权重与时间权重的集成，应用于对问题的综合评价分析。

1.时序加权平均算子的定义

令N={1,2,…,n},[μi,ai]为时序加权平均算子对，μi称为时间诱导分量，ai表示的是指标维度的数据量，定义时序加权平均算子为：

2.利用时序加权平均算子确定时间权向量

对时间赋权即为求时间权向量λ=(λ1,λ2,…,λp)T，本文采用规划问题的求解方法来求解时间权向量λ=(λ1,λ2,…,λp)T。首先引入时间权向量信息熵I和时间度γ

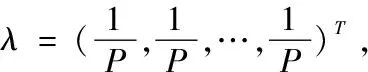
接下来我们求解规划问题：时间权向量中各元素的差异最小。在给定γ值时，可转化为求下面规划问题的最优解：

二、实例应用

(一)数据的来源与指标体系的构建

本文依据2014～2019年国内13家具有代表性银行的面板数据展开分析，分别包括5家大型商业银行和8家全国性股份制商业银行，这13家银行的总资产占银行整体资产的60%左右，在行业内具有较强的代表性。本文选取的指标数据均来自各大银行的年报。

本文依据指标体系的构建原则，充分考虑指标的全面性原则、科学性原则、重要性原则、可得性原则[3]，建立如下的指标体系：

表1 13家银行所构建的指标体系

(二)实例求解

建立如下的模型计算各银行的综合得分：

zki表示第k年第i个银行的综合得分，Zi表示第i个银行综合得分。

依据2019年13个银行的截面数据，进行初步分析。本文采用全序列极差化法来消除指标量纲的影响，Xij表示消除量纲之后的数据。

依据改进后的层次分析法(法一)、改进后的熵值法(法二)和基于博弈论赋权(法三)对上述8个指标进行赋权，如下表

表2 不同赋权法结果

依据时序加权平均算子方法，由于对银行的经营绩效进行评价，则前期数据相对更具有代表性，因此选取时间度ω=0.4，采用Lingo软件求解规划问题，得到时间权重λ

表3 时间赋权结果

按照上述过程，对13家银行的各个年份求综合得分，以及对年份加权，得到13个城市的最终得分以及排名，结果如下表：

表4 2014～2019年13家银行的得分及动态综合得分与排名

三、结论

从上述结果来看，基本每股收益、存款增长率、营业收入增长率是影响经营绩效的重要指标。8家全国股份制商业银行整体绩效要优于5家大型商业银行。国有5大银行实行的是一级法人治理结构下的多层代理体制，造成资产的管理有制度性的缺陷，在体制方面。远远落后于国外。在国有5大银行中，建设银行的排名最为突出，虽然建设银行的成立时间较晚，由于在动态评价中，更注重前期的数据，所以其综合得分较高，并且可以明显的看到建设银行在成长性和安全性方面明显优于其他国有银行，这与建设银行近些年在自动化方面的投入息息相关。招商银行作为我国目前最具有实力、规模最有优势的银行，在8家全国性股份制商业银行中处于领跑位置，在盈利性、安全性、成长性表现强劲。