结合平面投影与区域生长的点云表面重建

张晓帅，华顺刚

（大连理工大学机械工程学院，辽宁大连 116024）

0 引言

点云数据的表面重建是在已有点云数据的基础上还原空间点的几何拓扑结构，恢复物体模型的表面形状[1]。点云表面重建技术已经被广泛应用于制造业、医疗、文物保护以及地形测量等领域。随着技术手段的进步，获取的点云数据量越来越大，如何准确快速地处理这些数据，成为目前的紧要问题。

目前，表面重建的算法主要有Kazhdan[2]和刘涛等[3]提出的泊松算法；Kuo[4]和薄志成等[5]提出的区域生长法；Edelsbrunner等[6]提出的四面体法；Gopiy[7]和李凤霞等[8]提出的平面投影方法等。

本文提出一种平面投影与区域生长相结合的散乱点云曲面重建方法。通过局部点云离散度计算，自适应地选择不同的重建方法，提高了重建效率，减少了重建时间。

1 基于平面投影的点云表面重建

基于平面投影的点云重建是利用空间点云的局部平面性，将局部点集投影到二维平面上，再用平面三角剖分的算法生成三角形，最后将生成的三角关系还原回三维空间。该方法包括求取K邻域、平面拟合、平面投影、Delaunay三角剖分等几个步骤。

1.1 求取K邻域及其平面拟合

在对三维点云进行投影之前，要先获取目标点的K个近邻点，如果用遍历点集的方法来寻找，会导致搜索时间过长。本文采用包围盒法来加快寻找速度，其原理是先将空间划分成许多个小栅格，并为其编号。求中心点的K个临近点时，先在中心点所在的栅格内进行搜索，若得不到K个临近点，则进一步搜索临近的栅格[9]。

求得K邻域点集后，需要利用点集拟合一个二维平面，将空间点集投影到该平面上。本文采用最小二乘法来进行平面拟合。设其平面方程为z=ax+by+c，利用最小二乘法可以求解出平面参数。

1.2 二维平面投影及三角剖分

在求取出K邻域点集及其拟合平面后，应将这些点投影到拟合的二维平面上，对投影点进行二维的Delaunay三角网格化，最后将网格拓扑信息还原到三维空间中，生成空间网格模型，如图1所示。

图1 空间点的投影及其网格拓扑关系映射

1.3 投影法存在问题

平面投影的方法对于比较平滑的表面具有良好的重建效果，但有些情况下，投影生成的网格投射回三维空间时会发生失真。如图2所示，由于点云在空间中的密度分布不均匀导致重构过程中产生孔洞；由于投影重叠产生的错误拓扑关系等等。

图2 重建失真实例

为了避免基于投影的方法生成的网格映射回三维平面后发生严重失真，需要对点集的离散度进行判断，符合离散度要求的用平面投影来重建，不符合要求则采用区域生长法重建。

2 平面投影与区域生长相结合

本文利用局部点集的离散度来确定其重建方法，即通过偏移局部点集的拟合平面来生成两个平行平面，如果所有点都在两个平行平面之内，说明该部分点集离散度较小，可以用平面投影的方法重建该部分点集。如果存在某些点处于两个平行平面之外，则说明该区域的点集离散度过大，若用平面投影重建该部分点集，会产生较大的失真，应采用区域生长法进行空间三角形剖分。区域生长法在重建表面时，可利用各种原则来对第三点进行过滤，比较精确地还原模型的表面。

2.1 局部点集的离散度判断

判断点集离散度的上、下界面由拟合平面偏移得到，如图3所示。偏移量m用m=±β×dˉ来求解，dˉ为中心点与周围连接点距离的平均值；β是一个系数，可以通过其来调整偏移量的大小。实验证明，β取40%可以得到比较好的效果。如果存在某些点处于上、下界之外，则说明该区域的点集离散度不符合条件。

图3 局部点集在拟合平面附近的分布情况

实验表明，使用平面投影的方法可完成60%～70%的点云表面重建，如图4所示。这样，较平滑的部分已经重建完成，对于剩下的部分采用区域生长法进行重建。

图4 符合离散度要求的点集重建后的表面

2.2 区域生长算法改进

区域生长算法是从现有三角形的某一条边出发，基于某些优化判定准则，不断选择新的点与其构成新三角形，直到遍历所有点。常用的候选点筛选原则有最小内角最大原则、最大边长限制等。

为了提高重建后表面的质量，避免产生孔洞和错误的拓扑关系，本文对区域生长算法进行如下改进。

（1）增加拟合平面上空外接圆原则。利用候选点集与生长边的两个端点拟合一个平面，将这些点投影到拟合平面上，判断每一个候选点与生长边组成的三角形的外接圆应是否包含其他点，若包含其他点，则从候选点集中删去该点。如图5所示，当候选点C与生长边AB处于不同的表面时，其在拟合平面上的投影点所形成的三角形的外接圆会包含点D，因此应当在候选点集中去除点C，该方法可以防止出现错误的拓扑连接。

图5 局部点集及其在拟合平面上的投影

（2）分阶段进行重建。区域生长算法进行重建时，若最大边长和最小内角阈值过大，会容易生成错误的拓扑连接，降低模型表面的精确度；若阈值过小，则在点云稀疏的地方会因找不到满足条件的候选点而产生孔洞。因此本文的重建过程分两个阶段，第一阶段选取较小的阈值来保证重建表面的质量，然后选取较大的阈值进行第二次重建，以填补网格的孔洞。

3 实验结果及分析

为了验证提出算法的有效性，在Win7环境下用C++编写程序，使用OpenGL图形库对点云和网格进行渲染，使用MFC框架实现可视化界面。实验计算机配置为Intel（R）Core（TM） i5-4590 3.30 GHz CPU，8 G运行内存。表面重建的实例如图6所示。本文的算法在龙的嘴巴处可以很好地将上下颌分离开，点云比较稀疏的猫鼻子部分也没有孔洞出现。本文算法的细节部分处理得比较好，对于点云密度分布不均的区域也能够比较准确地进行表面重建。

4 结束语

本文算法结合了平面投影重建速度快和区域生长法准确度高的优点，把符合离散度条件的局部点集投影到二维平面上进行重建，降低了表面重建的复杂度，提高了表面重建的速度。用改进的区域生长法重建细节特征比较复杂、曲率变化比较大的部分，保证了重建表面的准确度。由于在区域生长算法中使用了拟合平面上空外接圆原则和分阶段重建的策略，避免了产生孔洞和错误的拓扑关系，保证了重建表面的完整性，提高了对点云模型的适应性。

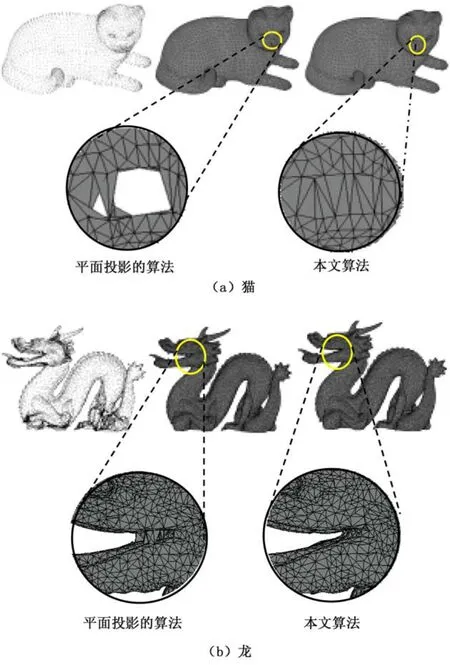
图6 重建实例