液压泵柱塞副油膜热-流耦合特性研究*
2020-07-23俞奇宽王冬云李胜虎荆宝德
俞奇宽,王冬云*,李胜虎,荆宝德
(1.浙江师范大学 工学院,浙江 金华 321004;2.杭州力龙液压有限公司,浙江 杭州 311228)
0 引 言
高速、高压工况下,因温度上升柱塞副油膜易被破坏,引起摩擦副组件干性摩擦而加速磨损[1]。
为此,国内外学者从宏观和微观的角度,对柱塞副的动力学特性和动压力的作用机理开展了系列研究[2-3]。WANG等[4]建立了柱塞副的运动学模型,探究了油膜厚度的变化规律;ZAWISTOWSKI T等[5]提出了用局部模型定义润滑间隙的数值模拟方法;SONG等[6]提出了稳态下柱塞油膜润滑特性的数值计算方法,并测量了油膜压力场分布;GELS等[7]开发了基于雷诺方程的油膜特性仿真方法,并提出了减少柱塞副能量损失的方法;MA等[8]研究了柱塞长度、间隙大小等参数对柱塞副泄漏和摩擦力的影响。Monika团队对柱塞副油膜温度场作了系统的研究:OLEMS等[9]提出了热-流耦合模型,并测量了柱塞副油膜固定点的温度;PELOSI等[10]提出了瞬态加载时的柱塞副热模型,分析了不同形式的缸体和材料对油膜厚度的影响;此外还提出了柱塞副热弹流润滑模型,并考虑了柱塞约束条件对热弹流润滑的影响[11-12];SCHENK等[13]将热弹流模型运用于滑靴副,拓宽了其应用范围。
国内外学者围绕柱塞副的优化开展了系统且深入的探索,然而,液压油温度对柱塞副最小油膜厚度、温度和动压力的影响有待进一步探究。
本文将建立柱塞副热-流耦合模型,并进行仿真,随后进行试验,总结不同入口油温下油膜温度场、厚度场的变化,来对模型加以验证,分析柱塞副中约束条件对热弹流润滑效应的影响。
1 柱塞副油膜热-流耦合模型
1.1 油膜厚度模型
柱塞的偏心量与油膜厚度关系如图1所示。
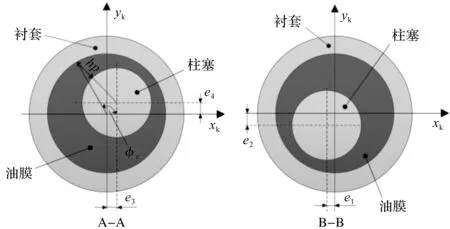
图1 柱塞的偏心量与油膜厚度的关系
柱塞的倾斜姿态可用柱塞轴线与柱塞腔中心线在两个端面的偏移量(e1,e2)及(e3,e4)进行表示。
再由几何关系可得XY平面内任一点油膜厚度hp为:
(1)
式中:ly—油膜在Y方向上的坐标;lf—油膜的长度;Dc—衬套直径;Dp—柱塞直径;Φc—油膜在柱塞周向的角度。
1.2 动压力模型
柱塞副油膜为层流,且呈“楔形”状,其动压力由雷诺方程[14-16]求解,如下式所示:
(2)
式中:hp—油膜厚度;p—油膜动压力;R—柱塞分布圆半径;μ—黏度;β—斜盘倾角;φ—柱塞转角;ω—柱塞自旋速度(约等于泵转速)。
此处雷诺方程的边界条件为:
(1)对于油膜的入口、出口和展开处分别有:
p(x,0)=pout,p(x,lf)=pin,
p(0,ly)=p(πDc,ly)
(3)
(2)在油膜的展开处的左端和右端应满足:
(4)
1.3 能量方程
柱塞副油膜可等效为热稳态流体[17],油膜温度通过能量方程求解。由于油膜厚度为微米级,可忽略z方向上的对流和扩散[18]。
因此,柱塞副油膜的能量方程可简化为二维方程:
(5)
(6)
式中:T—温度;cp—定压比热容;k—传热系数;ρ—液压油密度;ΦD—热源项;vx,vy—油膜在x和y方向上的速度,可由压力在厚度方向上积分算得。
此处能量方程的边界条件为:
(1)对于油膜的入口、出口和展开处分别有:
T(x,0)=Tout,T(x,lf)=Tin,T(0,ly)=T(πDc,ly)
(7)
(2)在油膜的展开处的左端和右端应满足:
(8)
1.4 黏温-黏压模型
动压力受黏度μ的影响,黏度μ又与温度和压力直接相关,因此需建立三者之间的耦合模型[19]。
本文采用Roelands方程[20]来描述:
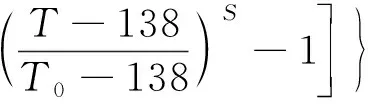
(9)
其中:
(10)
(11)
式中:α—黏压系数;β—黏温系数;μ0—环境黏度;T0—环境温度。
1.5 能量方程求解
笔者采用乘方格式进行离散[21]将展开后的油膜分别沿柱塞轴向和周向进行网格划分。
要获得能量方程的离散通式,需先对贝克列数Pe进行预估,经验算后x和y方向上的贝克列数都小于10,按乘方格式规定:
(12)
Fx=ρcpvpxΔy,Fy=ρcpvpyΔx
(13)
(14)
(15)
式中:Fx,Fy—在x和y方向上的对流系数;Dx,Dy—在x和y方向上的扩散系数;Pex,Pey—在x和y方向上的贝克列数。
经离散后的能量方程的通式为:
aPTP=aETE+aWTW+aSTS+aNTN+b
(16)
式中:aP,aE,aW,aN,aS—节点场变量系数;b—线性化源项。
各值计算方式具体如下:
(17)
本文采用CTDMA方法[22]进行计算,计算精度取εT=εp=1×10-7。
2 仿真与结果分析
本研究基于MATLAB建立了压力场和温度场的数值仿真程序,仿真计算流程如图2所示。

图2 仿真计算流程
主要计算流程为:
输入柱塞副几何参数和工况参数,求解柱塞初始位置和偏心速度;求解膜厚方程、雷诺方程和能量方程;以黏度随温度、压力变化前后是否小于设定精度和柱塞受力是否平衡为依据,判断得出温度、压力场的稳定性;当柱塞受力平衡时,柱塞旋转一定角度,进入下一计算周期,直至柱塞转过一周。
仿真主要物理参数如表1所示(其内主要包含有柱塞几何参数和液压油的物性参数)。

表1 仿真主要物理参数
油膜温度仿真结果如图3所示。
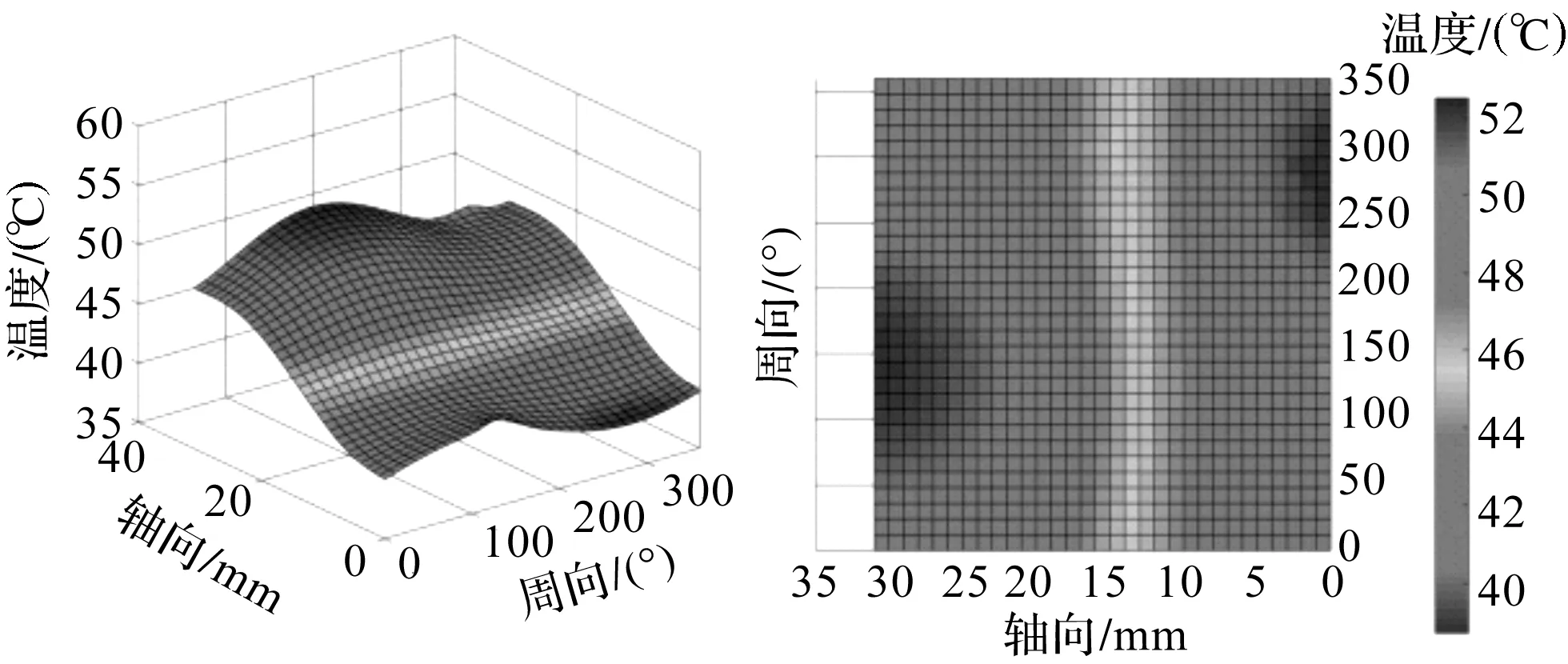
图3 油膜温度仿真结果(入口温度40 ℃)
图3中,从进口端到出口端温度逐步增加,在油膜的中段(轴向长度5 mm~25 mm之间)温度呈线性变化,油膜场最高温升达到了10 ℃;油膜两端有两个微小温升区,这是由于这两处为柱塞偏心量最大处,速度梯度最大,黏性耗散最高,即能量方程中的源项值为极大值,导致温度高于周围。
3 试验装置及测量结果分析
3.1 测试台总体结构与测试原理
为了验证模型的有效性,笔者探究油温对柱塞副油膜性能的影响,设计并搭建了一种360°柱塞副油膜特性测试台。
360°油膜特性测试台实物图如图4所示。

图4 360°油膜特性测试台实物图
该系统由变频电机驱动双联泵后输出高压油,驱动液压马达转动后带动斜盘旋转,实现测试箱体内柱塞的吸排油过程。通过变频器控制主轴转速,并通过扭矩-转速仪测量泵的输入转矩和转速,电涡流传感器、温度传感器和压力传感器测量油膜温度、压力和柱塞的偏心量。
测试箱体结构与功能如图5所示。

图5 测试箱体结构与功能1-斜盘;2-柱塞-滑靴组件;3-缸体;4-轴承座;5-涡轮-蜗杆组件;6-旋转接头;7-平衡柱塞;8-电涡流位移传感器;9-温度传感器;10-压力传感器;11-绕线盘;12-定滑轮;13-定滑轮;14-重物
测试箱体内轴测图如图5(a)所示,测试箱的位置已在图5中框出。测试时,研究人员将有一定压力的液压油引入缸体的柱塞腔中,将把柱塞-滑靴组件压在斜盘上以保证滑靴不被斜盘刮擦而损坏。开启驱动电机,待柱塞往复运动稳定后,启动步进电机,经齿轮和蜗轮蜗杆传动后使缸体转动,带动其上的传感器绕油膜一周,完成360°内油膜特性的测量。该过程中,3种传感器输出相对应的电压信号,信号在经过处理后即可得到油膜上对应角度的温度、压力以及柱塞的偏心情况。
传感器的安装示意图如图5(b)所示,且压力传感器和温度传感器皆为等间距分布。
缸体的尾端带有旋转接头,所以在保证液压油连续供给的同时保证缸体可自由转动。
绕线机构原理图如图5(c)所示,为了解决测量过程中的绕线问题,笔者设计了绕线盘,并在靠近地面的线缆上设置重物,使传感器导线一直处于“张紧”的状态,让线缆可以整齐收放。
3种传感器相关参数如表2所示。

表2 3种传感器相关参数
注:所有传感器满足量程和精度的要求
3.2 测量结果与仿真结果的对比
3.2.1 温度场实测与仿真结果的对比
不同温度入口温度下仿真与测量结果如图5所示。
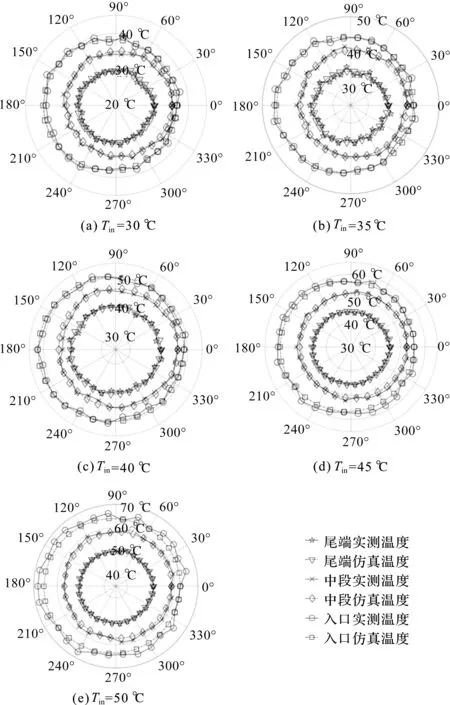
图5 不同温度入口温度下仿真与测量结果
基于前述试验台,本研究测量了转速为1 500 r/min,柱塞腔压力为20 MPa,入口油温为30 ℃~50 ℃时(间隔5 ℃为一组)3个特定位置圆周内油膜的温度。将测量结果和仿真结果放入极坐标内,对应实际柱塞角度,使结果更为直观。
由测试结果可知:在极坐标下油膜的入口处和出口处温度曲线明显凸起(所代表的极径变大),再至周围均匀减小,符合两端有温度凸起点和呈线性分布的仿真结论。
对比5组结果发现:当入口温度在40 ℃以下时,误差在±0.7 ℃之内,当入口温度增加至40 ℃以上时,出口温度的实测结果明显大于仿真结果,误差在-0.5 ℃~2 ℃之间。
造成这一现象的原因是:作为仿真边界条件的出口油温为测试箱体内的液压油油温,但当出口油温较高时,测试箱体油温与出口处油温的温差为2 ℃~3 ℃,导致仿真与实验差值加大。
3.2.2 温度对塞副油膜厚度的影响
最小油膜厚度处油膜所受力矩最大,偏心最为严重,容易发生干摩擦。
不同温度下最小油膜厚度随转角变化的情况如图6所示(转速1 500 r/min,柱塞腔压力20 MPa)。
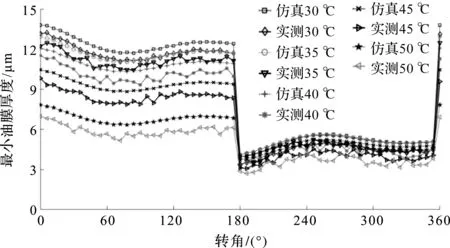
图6 不同温度下的最小油膜厚度随转角变化
其测量原理为,先通过位移传感器测得柱塞的偏心量,再由式(1)计算得到油膜厚度场,进而获得最小油膜厚度值。
对比不同温度下的最小油膜厚度随转角变化,结果可知:
(1)最小油膜厚度一般为几微米至十几微米,排油区的最小油膜厚度明显大于吸油区;
(2)在吸油区,柱塞腔的压力急剧减小,柱塞所受外力减少,相比于其他外力,离心力起主要作用。在其作用下,柱塞整体被甩向一侧,导致最小油膜厚度值明显减小,且在吸油过程中近保持不变;
(3)在排油区,最小油膜厚度先减小后增大。柱塞转至90°时,柱塞轴向速度最大,动压效应最强。但在力矩平衡方程中,此时外侧力矩更大,致使偏心量达到最大,最小油膜厚度为极小值。
此外,在测试过程中由于是间接测量,未考虑由温度、压力引起的柱塞和衬套的弹性变形,可引入以下公式进行修正:
h0=hp+Δhpp+ΔhTp+Δhpc+ΔhTc
(18)
式中:Δhpp,Δhpc—压力引起的柱塞和衬套弹性变形量;Δhtp,ΔhTc—由于热引起的柱塞和衬套弹性变形量。
上述所有量因为压力p和温度T的非线性,不能给出通用的计算表达式,但可通过有限元方法进行相应计算[23]。
对比图6中不同入口温度下的最小油膜厚度可知:
(1)在排油区,最小油膜厚度随入口温度上升而减小,但在吸油区变化不明显;
(2)当入口温度超过40 ℃时,排油区的最小油膜厚度减小趋势变得明显,减小幅度最大处达到3 μm;
(3)当入口温度超过45 ℃,排油区的最小油膜厚度大幅减小,说明液压油黏度大幅下降,入口温度上升量和最小油膜厚度减小量已不成线性关系,热平衡被破坏。
4 结束语
笔者建立了柱塞副油膜热流耦合模型,并基于MATLAB进行了仿真研究;搭建了柱塞副360°油膜特性试验台,验证了柱塞副油膜的热流耦合模型的有效性。主要结论如下:
(1)温度场在柱塞轴向呈“线性”分布,在油膜入口和出口处分别形成有微小的局部高温区。随着油温上升,液压油黏度下降,柱塞偏心量加大,且油膜最小厚度处产生压力高峰,柱塞达到新的动压平衡;
(2)在排油区,最小油膜厚度随温度逐步上升而减小。当入口温度超过40 ℃时,减小趋势加快,超过45 ℃时,吸油区的最小油膜厚度也开始减小,温度上升量与最小油膜厚度减小量不成线性关系,热平衡被破坏。因此,应将柱塞副的入口温度控制在45 ℃以下。
