全平衡卷扬式垂直升船机液压动态调平下的纵倾稳定特性研究*

张 阳，石端伟*，肖 童，程熊豪，周 吉

(1.武汉大学 水力机械过渡过程教育部重点实验室,湖北 武汉 430072；2.武汉大学 动力与机械学院,湖北 武汉 430072)

0 引 言

对于全平衡卷扬式垂直升船机，在运行过程中，由于提升卷筒圆度、钢丝绳直径、钢丝绳弹性模量制造误差等因素的影响，承船厢不可避免地会产生微量纵倾。为了调平承船厢以及均衡钢丝绳的拉力，研究人员设置了液压调平子系统。但是，由于液压调平子系统启动后会与主提升子系统、承船厢结构及厢内浅水晃动子系统构成复杂的机-液-固-流(MHSF)耦合系统，其动态稳定性以及抗承船厢倾覆的能力尚不清楚，目前仅允许液压静态调平[1-2](升船机停机后启动液压调平系统)。为了在安全运行的同时提高通航效率，研究液压动态调平(升船机运行过程中启动液压调平系统)下承船厢的纵倾稳定性十分必要。

国内针对卷扬式升船机耦合系统稳定性的研究中，阮诗伦[3]建立了船-水-厢耦合运动方程，并结合伽辽金法以及精细积分法进行了时域计算；程耿东[4]考虑提升钢丝绳、平衡重、承船厢、水体和船建立了耦合系统，利用自振频率为零时系统失稳为判据研究了稳定性。以上研究虽然考虑到了船-水-厢的耦合，但模型中对于纵倾稳定具有关键影响的主提升机械结构考虑并不完整，尤其缺少了同步轴这一关键结构；廖乐康[5]率先建立了主提升子系统、承船厢结构与厢内水体晃动的耦合动力学模型，并利用胡尔维茨定理判定了纵倾稳定性；程熊豪[6]在模型中补充了缺少的重力平衡重，并利用笛卡尔准则推导了临界吊点中心距计算公式。

虽然主提升子系统考虑趋于完善，但仍然缺少关键的转矩平衡重，且Housner理论对厢内浅水晃动子系统的模拟准确度有待提高。文献[7]利用多模态理论建立了浅水晃动子系统模型，完整考虑了主提升子系统与承船厢结构子系统模型，形成了机械-结构-流体耦合的动力学模型，并利用李雅普诺夫运动稳定性理论判断了纵倾稳定性，研究结果对于液压静态调平下的纵倾稳定性分析是适用的，但对于液压动态调平下形成的复杂MHSF耦合系统价值有限。

国内针对液压调平子系统的研究中，陆严[8-9]进行了比例物理模型试验研究，探索了模糊控制在自动调平问题中的适用性；王刚[10]建立了液压调平子系统的数学模型，提出了基于二分逼近法和积分同步法的承船厢调平控制策略。以上研究为调平控制策略提供了很好的参考，但均将液压调平子系统作为独立不参与耦合的系统进行了研究，对于液压动态调平的可行性探索是不利的。彭华伟[11]和潘尔顺[12]将液压调平子系统简化为一阶反馈系统，利用动态子结构法实现了液压调平子系统与其他子系统的动态耦合，并求解了动态响应。这对于MHSF耦合系统的研究是一个很好的尝试，但对于液压调平子系统的简化不利于动态特性的研究。

国外学者针对升船机的研究主要集中在工程设计及施工应用层面，对于升船机MHSF耦合系统的内在机理性研究尚处于空白。

本文针对液压动态调平下的全平衡卷扬式垂直升船机，首次建立包含主提升子系统、液压调平子系统、承船厢结构运动子系统以及浅水晃动子系统的MHSF耦合动力学模型；研究承船厢的纵倾稳定性；计算钢丝绳临界吊点中心距；分析各子系统的稳定特性及响应的快速性。

1 MHSF耦合系统模型

笔者将液压动态调平状态下的全平衡卷扬式垂直升船机简化为二维双吊点系统，用于探索液压动态调平下的承船厢纵倾稳定特性。

全平衡卷扬式垂直升船机的MHSF耦合动力学模型图如图1所示。

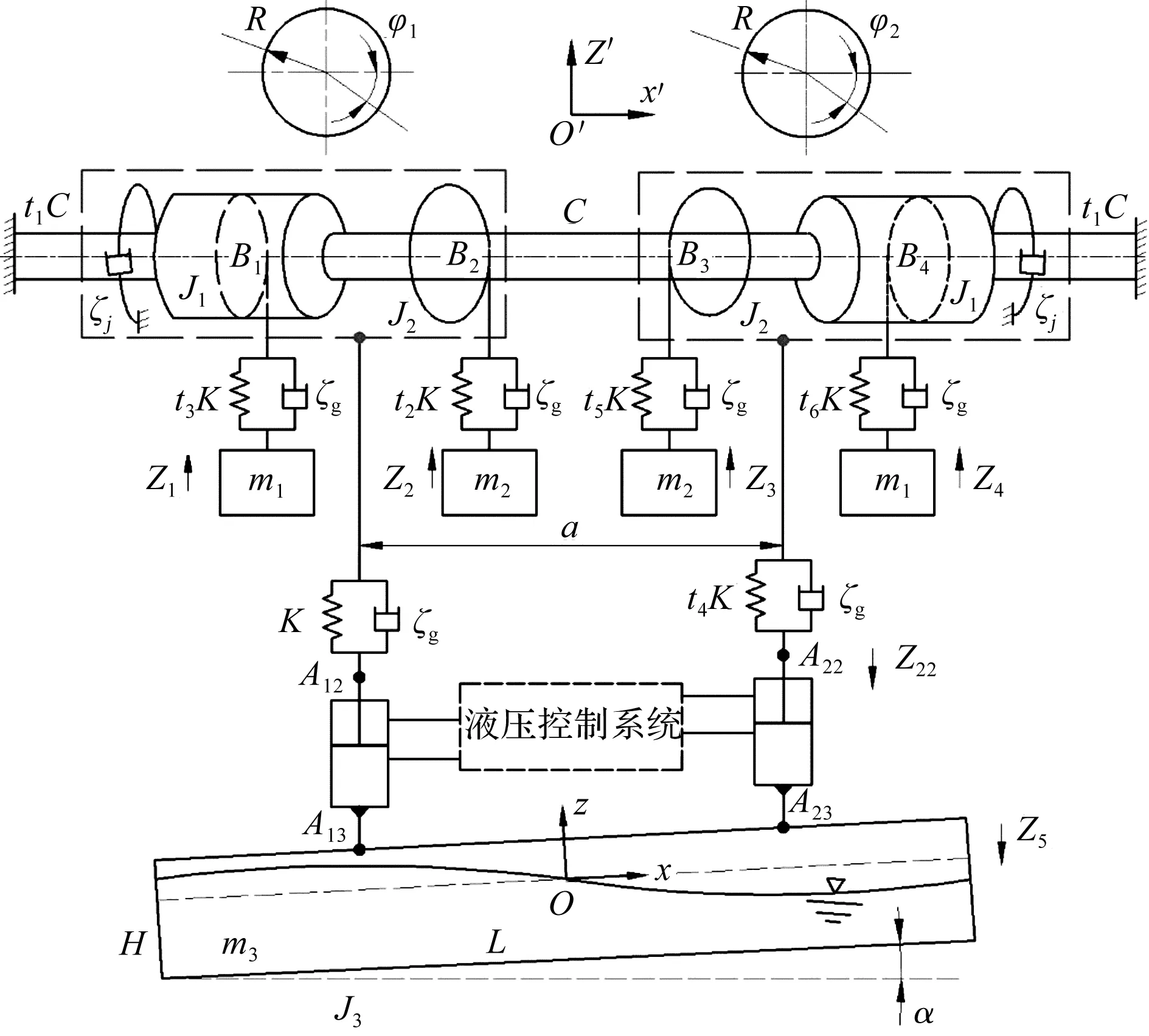
图1 全平衡卷扬式垂直升船机的MHSF耦合动力学模型R-卷筒和滑轮的半径；φ1-上游侧卷筒的转动角位移；φ2-下游侧卷筒的转动角位移；B1-上游侧提升卷筒；B4-下游侧提升卷筒；B2-上游侧滑轮；B3-下游侧滑轮；C-同步轴等效扭转刚度；t1C-电机传动轴等效扭转刚度；J1-卷筒的等效转动惯量；J2-滑轮的等效转动惯量；ξj-主提升机扭转振动阻尼比；ξg-钢丝绳僵性阻尼比；t2K-上游侧重力平衡重悬吊钢丝绳的等效刚度；t3K-上游侧转矩平衡重悬吊钢丝绳的等效刚度；t5K-下游侧重力平衡重悬吊钢丝绳的等效刚度；t6K-下游侧转矩平衡重悬吊钢丝绳的等效刚度；m1-转矩平衡重的一半；m2-重力平衡重的一半；Z1-上游侧转矩平衡重的位移；Z2-上游侧重力平衡重的位移；Z3-下游侧重力平衡重的位移；Z4-下游侧转矩平衡重的位移；a-钢丝绳吊点中心距；K-上游侧提升钢丝绳的等效刚度；t4K-下游侧提升钢丝绳的等效刚度；A12-上游侧提升钢丝绳下端与调平液压缸的铰接点；A22-下游侧提升钢丝绳下端与调平液压缸的铰接点；A13-上游侧调平液压缸与承船厢上端的铰接点；A23-下游侧调平液压缸与承船厢上端的铰接点；z22-调平液压缸活塞位移；Z5-承船厢在竖直方向的位移；H-承船厢水深；L-承船厢长度；m3-承船厢及厢内水体的质量；J3-承船厢及厢内水体的等效转动惯量；α-承船厢纵倾运动角度

1.1 浅水晃动子系统模型

根据文献[13]，在承船厢纵倾运动的影响下(见图1)，厢内水体的浅水晃动特性及产生的倾覆力矩可以表达为：

(1)

(2)

式中：M—浅水晃动产生的倾覆力矩；β1—浅水晃动的一阶模态函数；ρ—水体密度；ξ1—水体一阶边界层阻尼；ω1—浅水晃动一阶自振频率；g—重力加速度。

1.2 液压调平子系统模型

当承船厢在运行过程中出现图1所示纵倾时，水平传感器将水平偏差信号传输给控制器，控制器发出控制信号，经比例放大器放大后控制比例调速阀，经比例调速阀调节的液压油仅进入A22侧油缸有杆腔，A12侧油压不变，推动活塞向下运动，从而调平承船厢。

液压调平子系统主要包括：比例放大器、比例调速阀、四通阀控非对称液压缸和承船厢水平度传感器。其中，比例放大器工作频率远高于液压缸及承船厢的工作频率，简化为比例环节，即以控制器及D/A转换后的电压信号U为输入，电流I为输出，传递函数如下：

(3)

式中：Kα—比例放大器增益。

比例调速阀为电气元件，以电流I为输入，滑阀阀芯位移xv为输出，其响应速度比较快，与液压动力元件相比，动态特性可以忽略不计，视为比例环节。传递函数为：

(4)

式中：Ksv—比例调速阀的流量增益。

四通阀控非对称调平液压缸以阀芯位移xv为输入，活塞位移z22为输出。考虑弹性负载刚度、忽略液压缸泄漏情况下，四通阀控非对称液压缸的传递函数G(s)[14]为：

(5)

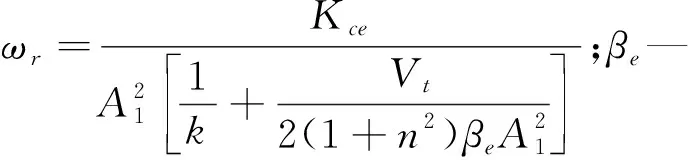
承船厢水平传感器以水平偏差Lα为输入，以电压U′为输出，传递函数如下：

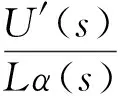
(6)

式中：Kf—传感器增益。

综上，液压调平子系统闭环传递函数方框图如图2所示。

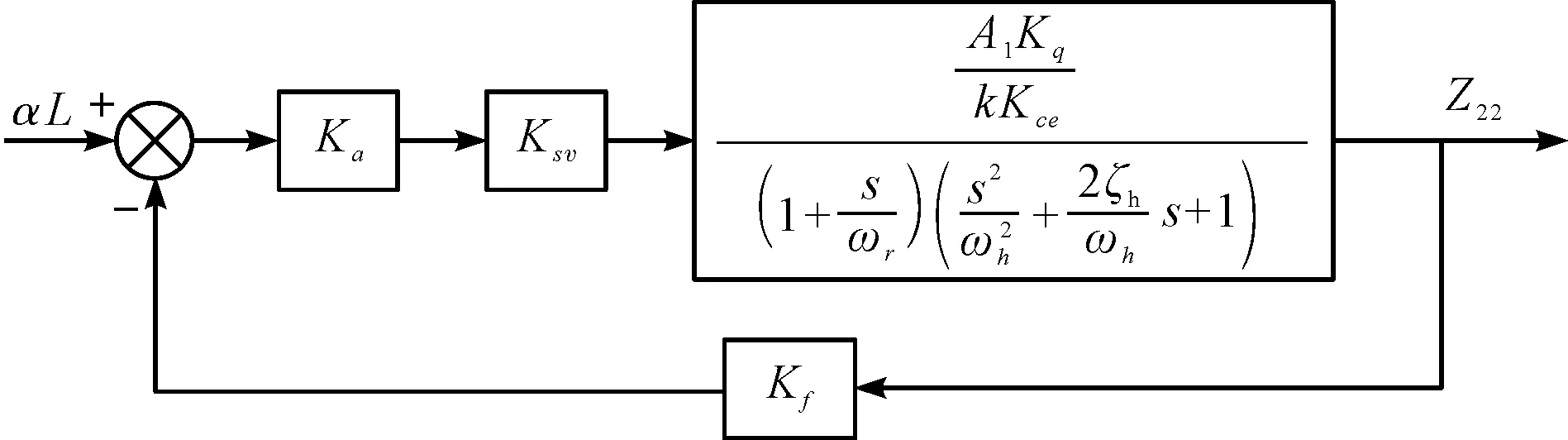
图2 液压调平子系统闭环传递函数方框图

由图2可知，液压调平子系统的闭环传递函数GB(s)为：

GB(s)=

(7)

则，液压调平子系统的微分方程为：

(8)

1.3 主提升机械子系统模型

从图1可得，主提升机械子系统和承船厢结构子系统的动能与势能分别为：

(9)

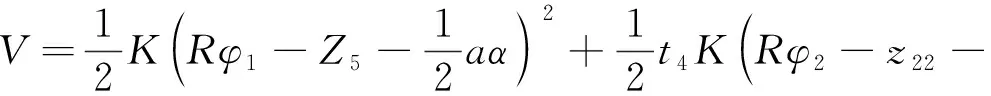
(10)

式中：t1—同步轴与电机传动轴的扭转刚度比；t2—上游侧重力平衡重悬吊钢丝绳弹性模量容差和提升扬程的影响系数；t3—上游侧转矩平衡重悬吊钢丝绳弹性模量容差和提升扬程的影响系数；t5—下游侧重力平衡重悬吊钢丝绳弹性模量容差和提升扬程的影响系数；t6—下游侧转矩平衡重悬吊钢丝绳弹性模量容差和提升扬程的影响系数；t4—上、下游侧钢丝绳之间弹性模量制造误差的影响系数。

根据第二类拉格朗日方程可得主提升子系统动力学模型，即：

(11)

(12)

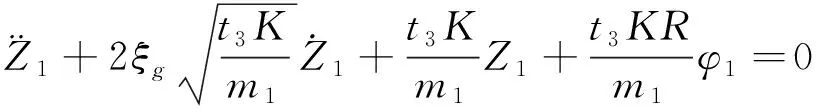
(13)

(14)

(15)

(16)

1.4 承船厢结构子系统模型

结合式(9～10)，根据第二类拉格朗日方程，可得承船厢结构子系统的动力学方程，即：

(17)

(18)

式中：ξp—升船机承船厢纵倾运动阻尼比；ξv—升船机承船厢竖向运动阻尼比。

1.5 MHSF耦合系统动力学模型

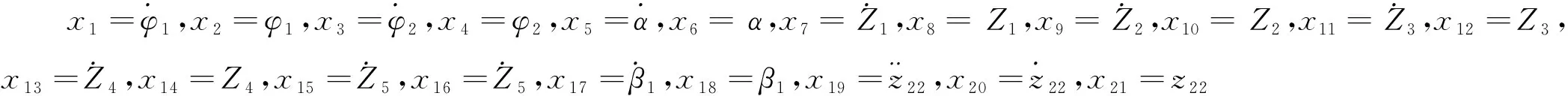
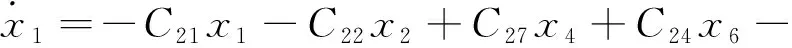
(19)

(20)

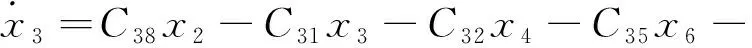
(21)

(22)

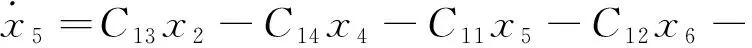
(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

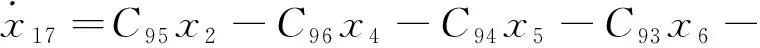
(35)

(36)

(37)

(38)

(39)

式中：Cij—式(1～2，8，11～18)化简为式(19～39)过程中，各参数前的系数表达式。

2 临界吊点中心距计算

临界吊点中心距是指耦合系统临界稳定状态下对应的吊点中心距，是评价纵倾稳定性的重要指标；临界吊点中心距越小说明稳定性越高。

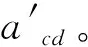
通过两种不同方法计算得到的四座典型全平衡卷扬式垂直升船机不同工况的临界吊点中心距，如表1所示。

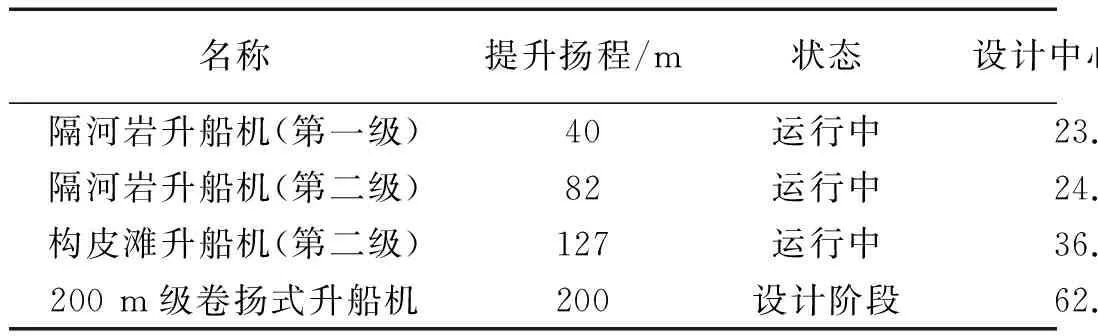
表1 四座典型全平衡卷扬式垂直升船机不同工况的临界吊点中心距

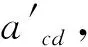
(2)表1中，acs为液压静态调平下保持纵倾稳定对应的临界吊点中心距；比较acd与acs可以看出，相比较于液压静态调平，液压动态调平会降低承船厢的纵倾稳定性。主要原因是液压调平系统以串联的方式耦合进入原机械-结构-流体系统，降低了系统的整体刚度；

(3)将acd与设计中心距作比较可以看出，在液压动态调平下，四座卷扬式升船机的设计吊点中心距均依然能够保证升船机承船厢处于纵倾稳定状态。尤其是对于200 m级升船机，设计参数可以保证即使在最危险位置开启动态调平，安全系数依然有1.1(62/56)，承船厢仍然能够稳定安全运行。

3 纵倾稳定特性分析

3.1 子系统稳定特性分析

吊点中心距a=56 m时，200 m级升船机各子系统位移响应图如图3所示。

分析图3可知，吊点中心距取临界值56 m时，浅水晃动子系统响应呈现等幅振荡，为临界稳定状态；其余各子系统收敛，处于稳定状态。即浅水晃动子系统是最易受吊点中心距影响，而不稳定的。

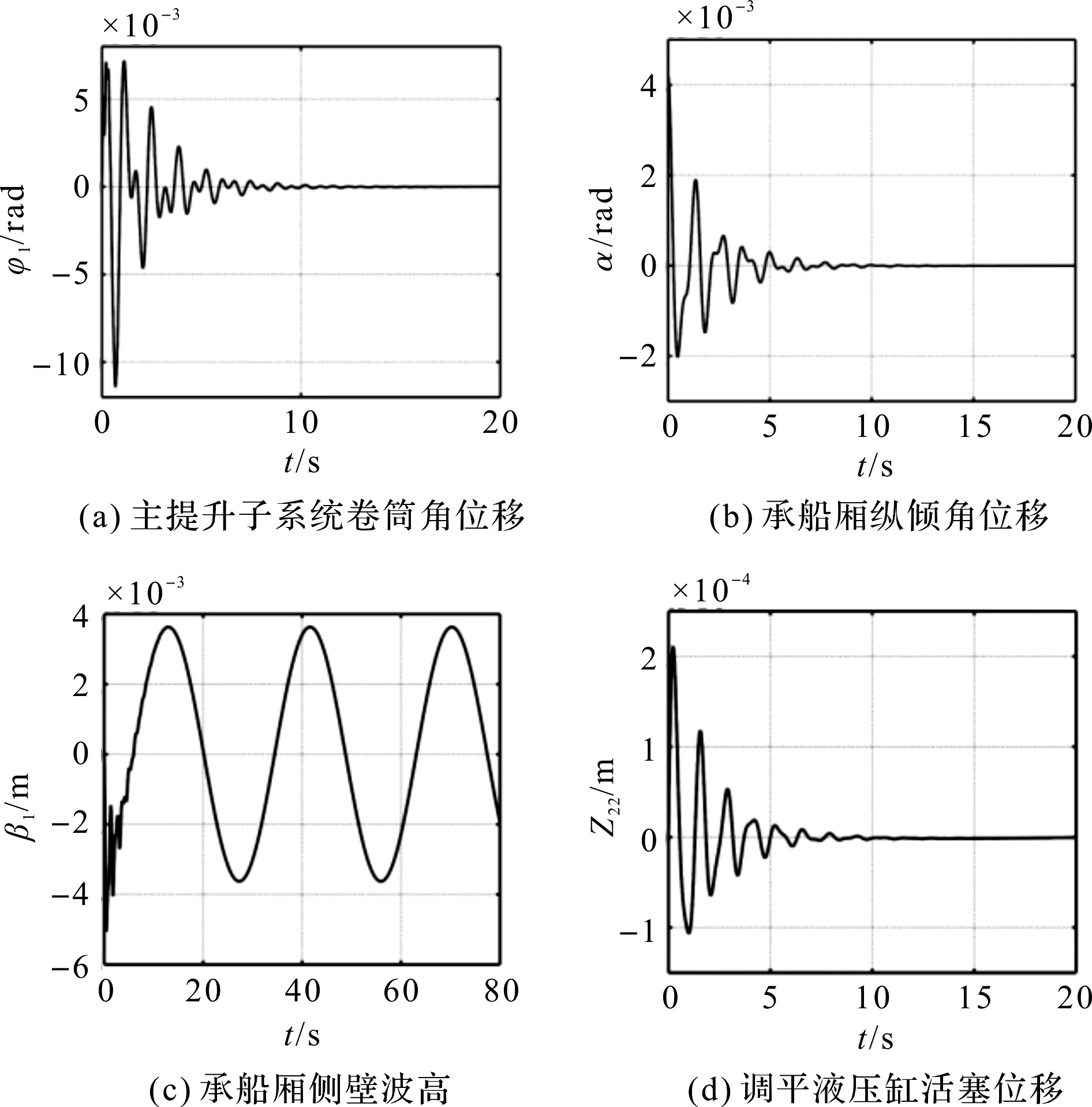
图3 a=56 m时200 m级升船机各子系统位移响应

吊点中心距a=19 m时，200 m级升船机各子系统位移响应图如图4所示。

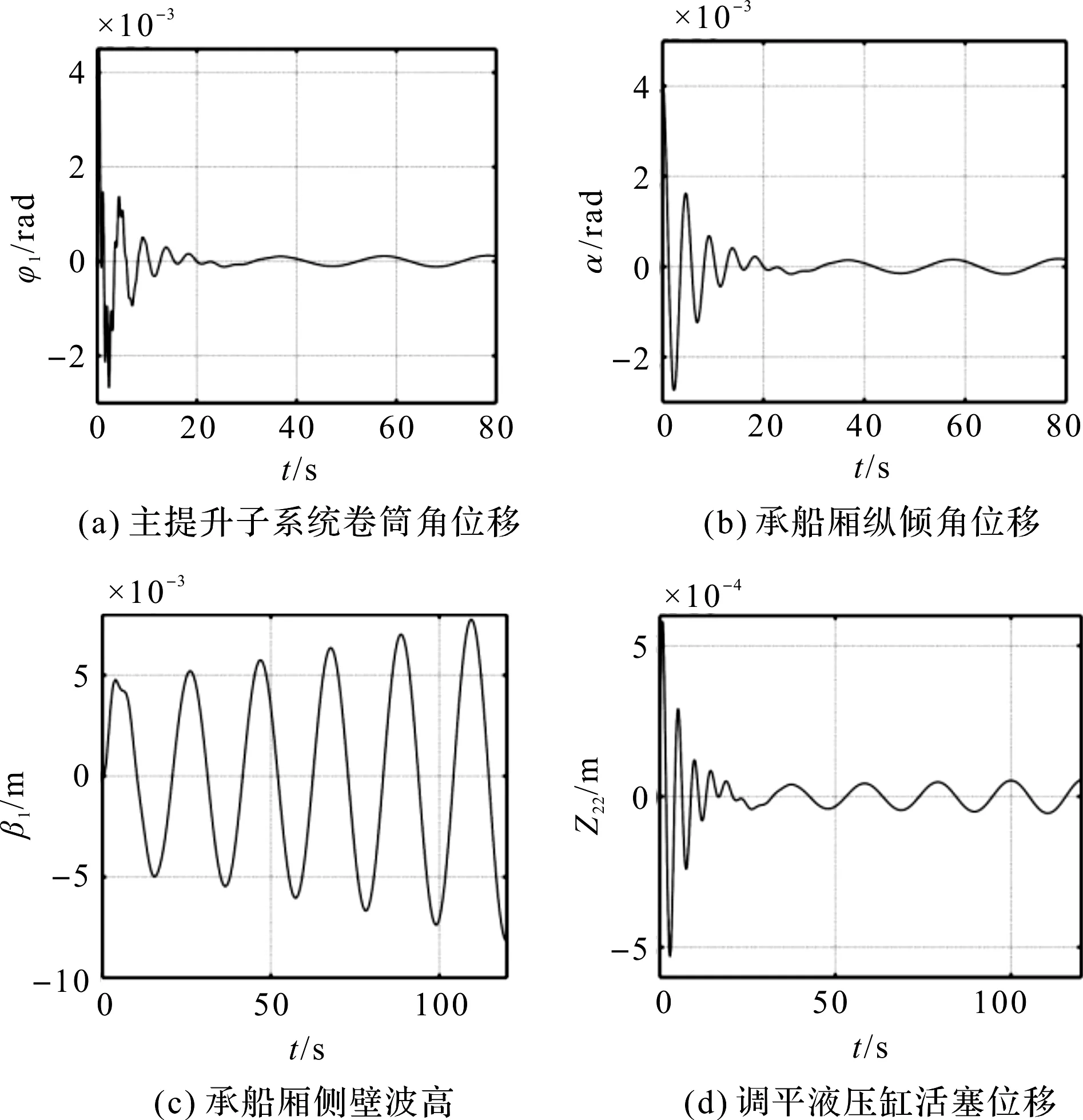
图4 a=19 m时200 m级升船机各子系统位移响应

分析图4可知，当吊点中心距降至19 m时，浅水晃动子系统已经发散，其余各子系统位移响应呈现等幅振荡，处于临界稳定。此时虽然MHSF耦合系统已经纵倾不稳定，但悬吊的承船厢不会出现倾覆。

吊点中心距a=18.5 m时，200 m级升船机各子系统位移响应图如图5所示。

图5 a=18.5 m时200 m级升船机各子系统位移响应

图5中，若吊点中心距低于19 m时(取18.5 m)，处于临界稳定的主提升子系统、承船厢结构子系统以及液压调平子系统的位移响应会慢慢趋于发散；出现大幅度不可逆倾覆所需的时间随吊点中心距的降低而缩短。

3.2 子系统响应快速性分析

以200 m级卷扬式垂直升船机为对象，根据工程实际，给定初始状态纵倾角0.004 2 rad。

吊点中心距a=62 m时，200 m级升船机各子系统位移响应图如图6所示。

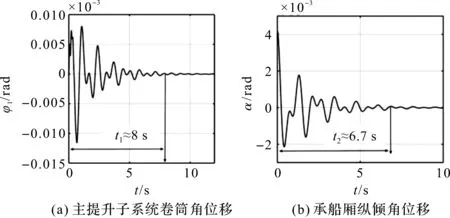
图6 a=62 m时200 m级升船机各子系统位移响应

图6中，t1～t4分别表示对应各子系统从开始响应到进入工程误差允许范围内的稳态所需的调整时间。由图6可知，浅水晃动子系统的响应快速性是最差的(t3>10 s)；其次就是主提升系统(t1≈8 s)；再是承船厢结构子系统(t2≈6.7 s)；响应快速性最好的是液压调平子系统(t4≈5.4 s)。

4 结束语

为研究全平衡卷扬式垂直升船机承船厢在液压动态调平下的纵倾稳定性，本文建立了包含主提升机械子系统、液压调平子系统、承船厢结构子系统与浅水晃动子系统的MHSF耦合动力学模型；利用变步长龙格库塔法求解时间响应，以响应的收敛性为判据得到了临界吊点中心距；以四座典型全平衡卷扬式升船机为例，验证了模型及方法的可靠性；分析了各子系统的稳定特性与响应快速性。

研究结果表明：

(1)对于全平衡卷扬式垂直升船机，与液压静态调平相比，液压动态调平虽然会降低纵倾稳定安全裕度，但依然能够保证承船厢运行过程中始终处于纵倾稳定状态；

(2)对于200 m级卷扬式垂直升船机，在液压动态调平状态下，目前的设计中心距62 m可以保证纵倾稳定安全系数不低于1.1；即使设计吊点中心距略低于临界值56 m，水体晃动缓慢趋于发散，但承船厢依然能够维持运行；只有设计吊点中心距低于19 m时，承船厢才会出现倾覆；

(3)200 m级卷扬式垂直升船机承船厢受到纵倾影响后，各子系统响应调整至稳态的速度由快到慢依

次为：液压调平子系统、承船厢结构子系统、主提升子系统、浅水晃动子系统。