利用Laplace变换求解分数阶Allen-Cahn方程

汪精英， 邓杨芳， 翟术英

(华侨大学 数学科学学院， 福建 泉州 362021)

1 预备知识

Allen-Cahn方程是一类非齐次半线性泊松方程[1]，是材料科学中描述流体动力学问题和反应扩散问题的一类重要方程.在研究图像处理[2]、平均曲率流量[3]、晶体生长[4]、人群扩散现象[5]和随机扰动[6]等问题时，Allen-Cahn方程发挥着极为重要的作用.

考虑时间分数阶Allen-Cahn方程,即

(1)

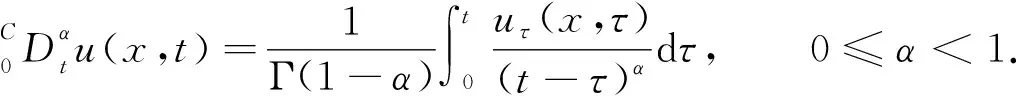
(2)

Allen-Cahn方程可以视为Lyapunov能量泛函的L2梯度流[7].设基本能量泛函为E(u)，即

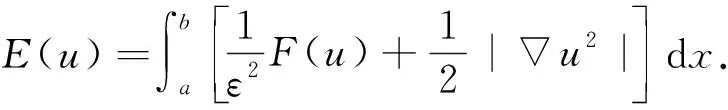
(3)

能量泛函E(u)关于时间t求Caputo型分数阶导数为

由此易知,能量泛函E(u)不会随时间的增长而增加.

求解上述方程数值解的方法很多[8-20].文中利用Laplace变换法[20]逼近时间分数阶Allen-Cahn方程(1)，并将其转化为整数阶问题.然后，对所得到的整数阶Allen-Cahn方程，采用算子分裂法[14]将方程分裂为线性部分和非线性部分，并将解算子分别记为SA和SB.上述方程可通过以下格式求解，即

(5)

式(5)中：线性部分利用C-N格式求解，非线性部分解析求解，从而达到减少计算量的目的，且得到简单有效的数值格式.

2 分数阶Allen-Cahn方程的数值解

2.1 利用Laplace变换将分数阶问题转化为整数阶问题

先用Laplace变换逼近Caputo型分数阶导数，即

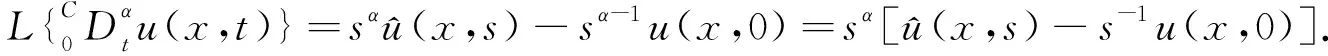
(6)

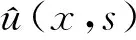
sα≈αs1+(1-α)s0=αs+(1-α).

(7)

将式(7)代入到式(6)，可得

再利用Laplace逆变换,可得

(9)

从而原分数阶Allen-Cahn方程可转化为整数阶方程，即

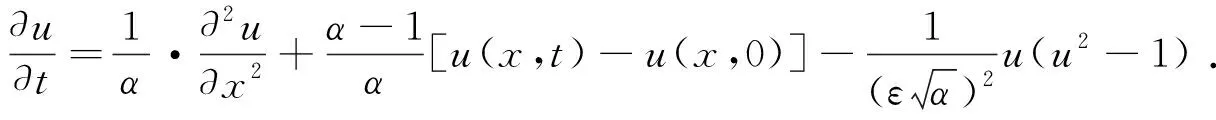
(10)

2.2 算子分裂法求解Allen-Cahn方程

利用算子分裂将Allen-Cahn方程分解为热传导方程和非线性方程，即有

(11)

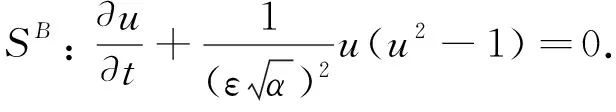
(12)

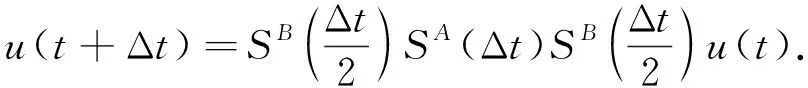
(13)

非线性方程解析求解，其数值格式为

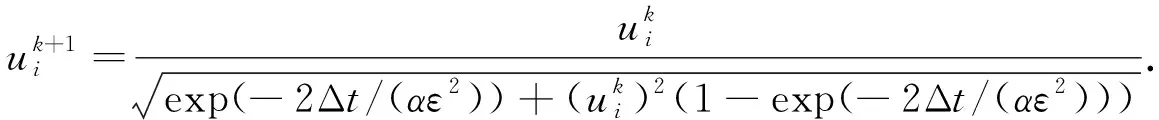
(14)

引入二阶中心差分算子，则有

(15)

热传导方程的C-N格式为

(16)

将式(15)代入式(16)中，进一步化简,可得

结合式(13)，(14)和(17)，可得到求解问题(10)的二阶差分格式为

(18)

注1Laplace变换同样可以用来逼近Riemann-Liouville型分数阶导数， 而且p(>0)阶Riemann-Liouville分数阶导数的Laplace变换为

(19)

3 数值算例

通过数值算例，验证数值格式的有效性和精确性.为方便分析，对如下符号进行解释

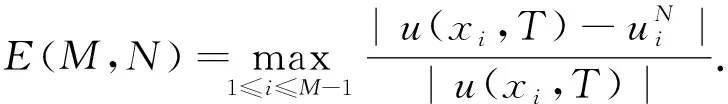
(20)

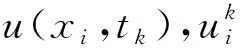
3.1 算例一

为验证时间数值计算的精度，选取具有充分正则性的精确解的方程作为测试实例.考虑如下Allen-Cahn方程，有

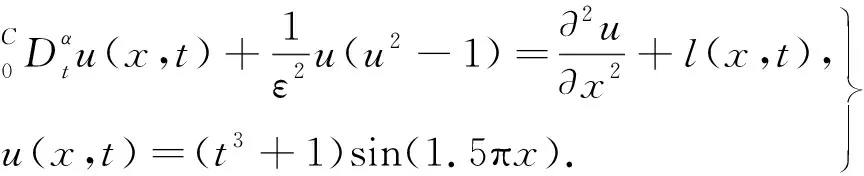
(21)

在式(21)右端添加l(x，t)，则

是为了满足给定的方程及其精确解.其区域的取值范围是[0，1]×[0，1]，ε=0.5.

取网格剖分M=20，N=3 000，给出α为0.5时的数值解和误差(e)图像,分别如图1,2所示.

图1 算例一的数值解图像(α=0.5) 图2 算例一的误差图像(α=0.5) Fig.1 Numerical solution image of example 1 (α=0.5) Fig.2 Error image of example 1 (α=0.5)

分别计算不同剖分、不同ε和不同α时的最大相对误差，结果如表1所示.

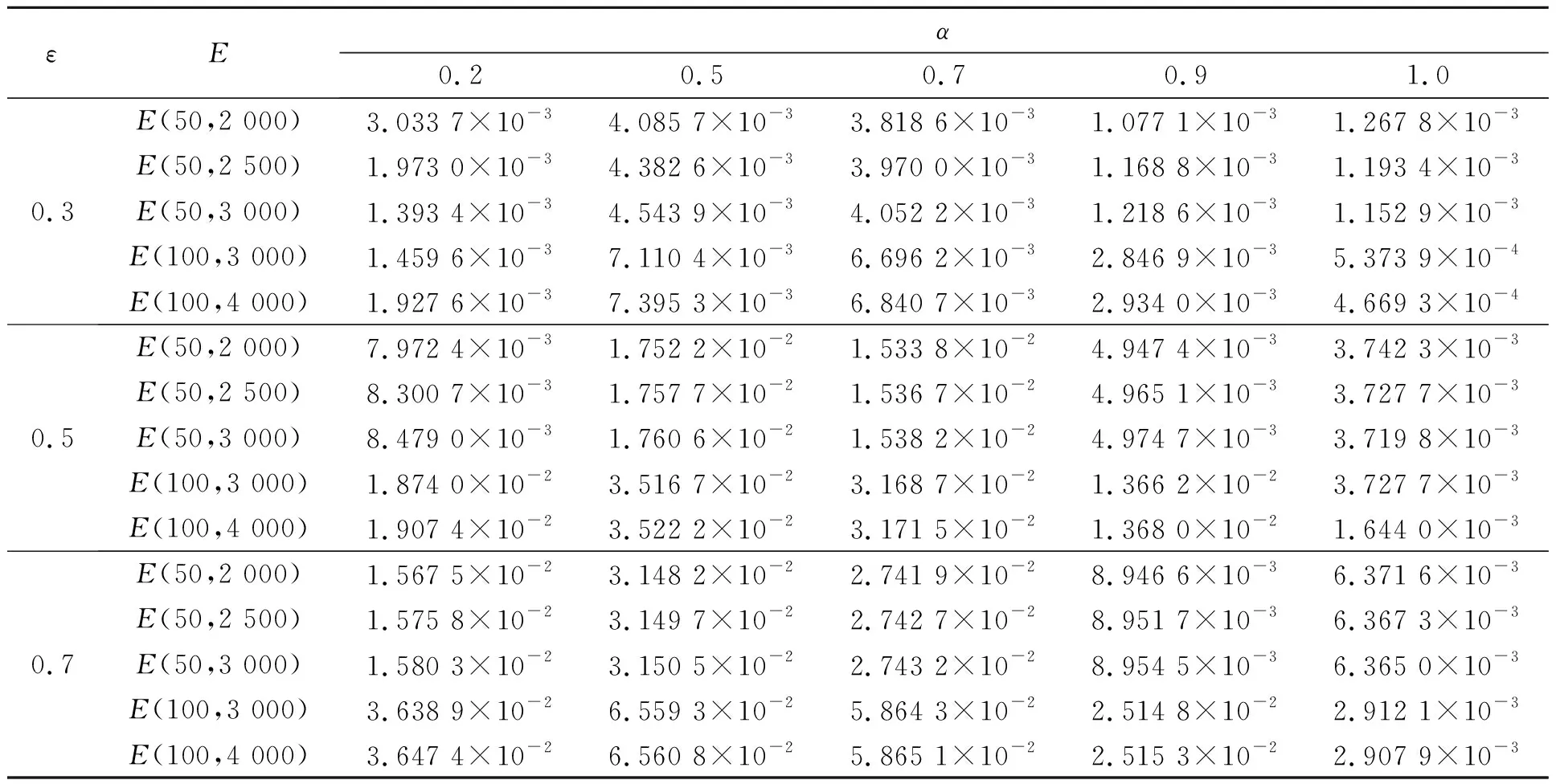
表1 不同ε时的最大相对误差Tab.1 Maximum relative error at different ε

由图1，2可知：数值解逼近于精确解，具有较高的精度.由表1可知：数值解在不同剖分、不同ε及不同α时均满足精度要求，α越接近1，ε越小且网格剖分越细密，数值解精度越高.

3.2 算例二

考虑如下初值问题

u(x，0)=ε·sin(1.5πx)，x∈[-1，1].

取Dirichlet边界条件，左边界u0=1，右边界uM=-1，t∈[0，T].定义离散能量函数为

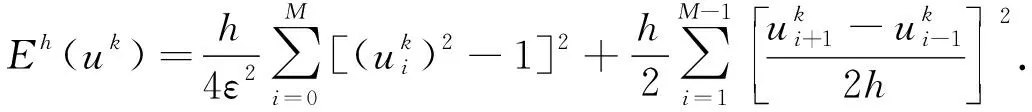
(23)

具体求解参数为M=20，N=1 000，T=2，ε=0.1，并分别取α=0.2，0.5,0.9，得到不同α的数值解和能量变化图像,分别如图3～8所示.

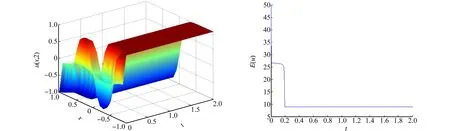
图3 算例二的数值解图像(α=0.2) 图4 算例二的能量变化图像(α=0.2)Fig.3 Numerical solution image of example 2 (α=0.2) Fig.4 Energy change image of example 2 (α=0.2)

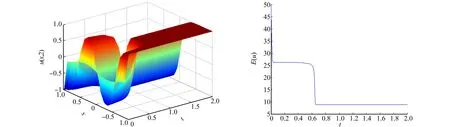
图5 算例二的数值解图像(α=0.5) 图6 算例二的能量变化图像(α=0.5)Fig.5 Numerical solution image of example 2 (α=0.5) Fig.6 Energy change image of example 2 (α=0.5)

图7 算例二的数值解图像(α=0.9) 图8 算例二的能量变化图像(α=0.9)Fig.7 Numerical solution image of example 2 (α=0.9) Fig.8 Energy change image of example 2 (α=0.9)

由图3～8可知:能量函数E(u)随着时间t的增大而减小，即能量泛函E(u)满足能量递减.此外，时间分数阶Allen-Cahn方程的能量耗散受分数阶α的影响，α越小，能量衰减越快.

4 结束语

利用Laplace变换，将时间分数阶Allen-Cahn方程转化为整数阶Allen-Cahn方程;然后，再利用算子分裂法得到能量稳定的二阶差分格式;最后，通过数值算例验证了格式的有效性.