采用Bootstrap抽样的靖远黄河大桥模态参数识别不确定性量化
2020-07-23刘远贵徐乐赖芨宇骆勇鹏
刘远贵, 徐乐, 赖芨宇, 骆勇鹏,2
(1. 福建农林大学 交通与土木工程学院, 福建 福州 350002; 2. 华侨大学 福建省结构工程与防灾重点实验室, 福建 厦门 361021)
模态参数是结构的基本动力参数之一,可用于荷载识别、损伤诊断、模型修正及既有结构状态评估等方面[1].常用的模态参数识别方法有频域法、时域法和时频分析3类.基于随机子空间的模态参数识别是时域模态参数识别中较为常用的方法.该方法可直接作用于时域数据,无需转化为频域数据,避免频率分辨率误差的问题[2].由于结构动力测试受仪器精度、测量误差、噪声干扰等因素的影响,模态参数识别结果具有一定的不确定性[3],从而影响结构荷载识别、损伤诊断及状态评估结果的精度.因此,如何有效地评估模态参数识别结果的可信程度引起学者的关注.蒲黔辉等[4]采用特征系统实现算法,对整个模态识别算法进行摄动分析,从而确定模态参数对测量误差的灵敏度.秦世强等[5]通过构建模态参数置信区间的方法衡量模态参数的不确定度.易伟建等[6]采用贝叶斯方法研究模态参数的不确定性.Döhler等[7]提出一种有效估计模态参数协方差的算法,通过一阶摄动分析对识别结果的不确定性进行评估.Herrera等[8]研究模态参数在1年内的数据监测变化,并对识别结果进行量化.上述方法是在假设模态参数服从的概率分布函数及分布参数已知的情况下进行的评估.然而,在实际振动测试中,由于观测数据有限及激励荷载的不确定性,观测数据样本服从的概率分布往往未知,当人为假设的概率分布与实际不符时,模态参数识别结果的准确性将受到影响.
Bootstrap是一种有返还的再抽样统计方法,可用于总体分布未知或统计量分布未知时的参数推断,在一定程度上可解决上述问题,但该方法在模态参数识别不确定性量化方面的研究还较为少见.Farrar等[9]采用蒙特卡罗(Monte Carlo)和Bootstrap抽样对模态参数置信区间的算法进行比较,通过模态参数估计算法,得到模态参数集合,从而得到其统计分布.Chauhan等[10-11]将Bootstrap抽样引入模态参数估计过程中,阐述Bootstrap抽样的特点及其在模态参数识别不确定性量化中的应用可行性.Yaghoubi等[12]联合相关分析和Bootstrap抽样,实现模态参数自动估计,提高参数识别的精度和自动化程度.本文采用协方差驱动随机子空间(SSI-COV)法对靖远黄河大桥的模态参数进行识别,并引入Bootstrap抽样,分别从整体和局部对靖远黄河大桥的模态参数识别结果的可靠性进行评价.
1 基本理论
1.1 系统状态空间模型
结构系统振动方程可描述为
(1)
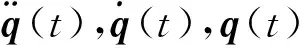
在环境激励下,实测数据总是离散的,应将连续的状态空间方程离散化,即
xk+1=Axk+Wk,yk+1=Ccxk+Vk.
(2)
式(2)中:xk+1,yk+1分别为k+1时刻系统的状态向量和输出向量;A为状态矩阵;Cc为输出矩阵;xk为k时刻系统的状态向量;Wk,Vk分别为零均值的过程噪声和测量噪声,且互不相关.
1.2 随机子空间识别理论
随机子空间(SSI)法是一种时域内线性系统识别算法[13],无需进行傅里叶变换,直接对时程响应数据进行处理,可以有效地从环境激励的结构响应中提取结构模态参数.SSI法主要分为数据驱动随机子空间(SSI-DATA)法与协方差驱动随机子空间(SSI-COV)法两类.首先,协方差驱动随机子空间法将输出数据的协方差组成Toeplitz矩阵;然后,对该矩阵进行奇异值分解(SVD),得到扩展的可观测矩阵和可控矩阵;最后,利用其性质计算系统的A和Cc,进而得到结构的模态参数.该算法有以下6个流程.
1) 构建Hankel矩阵,即
(3)
2) 根据白噪声均值为零且互不相关的性质,计算输出协方差矩阵Ri,有
Ri=E[yk+iyk].
(4)
式(4)中:E为数学期望.
3) 将协方差序列组成Toeplitz矩阵并进行分解,有
(5)
式(5)中:G为下一时刻的状态向量与输出向量的协方差矩阵.
4) 对Toeplitz矩阵进行奇异值分解,可得
(6)
式(6)中:Oi为系统可观矩阵;U,V均为对协方差矩阵进行奇异值分解后形成的正交矩阵;S为奇异值分解中正奇异矩阵组成的对角阵;U1,U2均为对应于非零奇异值的左奇异向量构成的正交矩阵;V1,V2均为对应于非零奇异值的右奇异向量构成的正交矩阵;S1为降序的奇异值构成的对角阵.
5) 计算得到系统状态矩阵A和输出矩阵Cc,并对A进行特征值分解,可得
A=ΦΛΦ-1.
(7)
6) 将离散系统转化为原连续系统,系统特征值也相应变化,则由
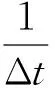
(8)
可计算出结构第m阶模态参数,即
(9)
式(8),(9)中:Δt为采样时间间隔;i为虚数单位;am,bm分别为系统特征值的实部和虚部;fm,ξm分别为第m阶的固有频率和第m阶的阻尼比.
结构第m阶模态的观测振型φm是系统状态矩阵A的特征向量Φm的可观部分,即
φm=CcΦm.
(10)
1.3 模态参数不确定性量化
在传感器数量有限的情况下,需要采用多个测试组分批次进行振动测试,才能获得结构的整体振动特性.受外界因素、仪器误差影响,基于多组模态测试识别得到的模态参数不尽相同.因此,需有效地评价每个测试组识别的模态参数的可信度,特别是在测试组有限的情况下,基于有限的数据评价识别得到的模态参数的可信度,并进一步确定结构模态参数的最终结果[14-15].
Bootstrap 抽样运用模拟再抽样技术代替理论分析,基于有限的试验观测数据,模拟再抽样出大量符合原数据特征的模拟样本,从而提供足够的样本进行概率统计分析[16],避免统计分析对概率分布函数假定的依赖.因此,提出一种基于Bootstrap抽样的结构模态参数识别结果不确定性量化分析方法.该方法有以下4个计算步骤.
步骤1基于不同测试组的加速时程响应,采用SSI方法,可识别到多组模态参数X=(x1,x2,…,xN),假设其为总体分布F的一个随机独立样本,样本容量为N.根据该样本,可构造原始样本的经验分布函数Fn(x),即
(11)
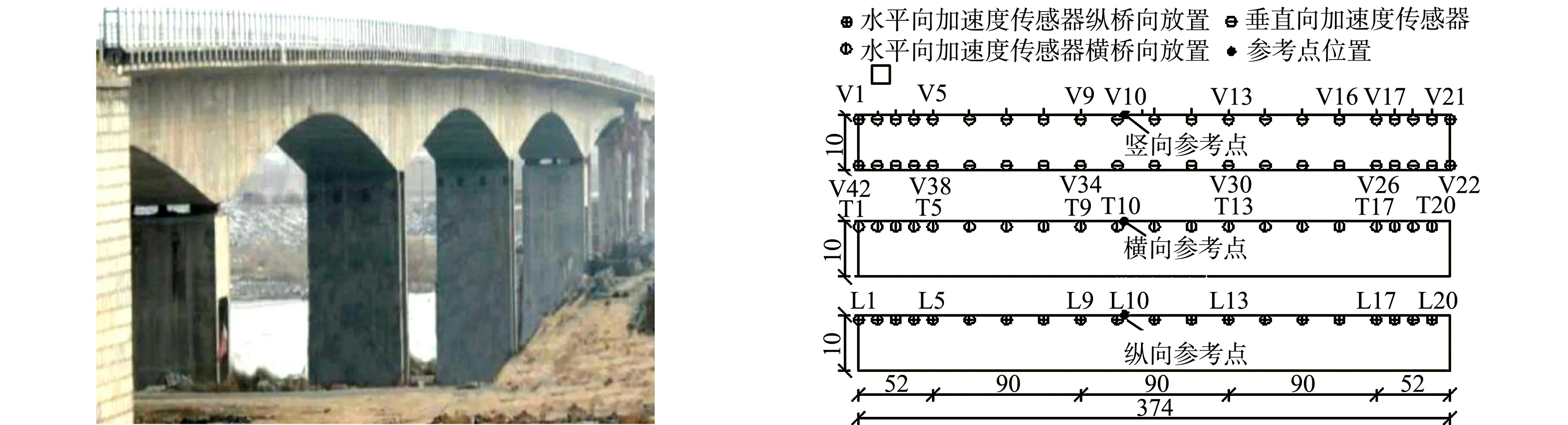
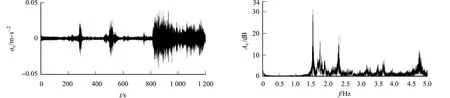
式(11)中:x(1) (12) (13) (14) (15) 在统计学上,平均值数量等同于描述总体的样本的大小.因此,平均值数量越多,越接近准确的估计值,即样本规模的增大可以减小方差.以B个自助样本均值的均值作为频率识别值减少了随机误差,均值的方差可以反映各测点识别的频率值的整体变异程度和稳定性,方差越大,表明多个测试数据识别的模态参数的不确定性越大;反之,方差越小,则不确定性越小. 为了评估基于单个测点的数据识别得到的模态参数的不确定性,首先,将单个测试组数据按采样时间分为m个时间段,可以得到m组识别结果;然后,采用上述方法对m组识别结果进行统计分析,进一步评估基于单个测点识别得到的模态参数的可靠性;最后,将单个测点的识别值与多测点的识别值进行比较,通过均值可以得出结构模态参数识别值的差异程度,通过方差可以分析结构模态参数整体和局部的离散程度,进而为模态参数识别的准确度和稳定性提供可靠性指标. 以靖远黄河大桥[17]环境振动测试为例,验证文中方法的可行性和可靠性.靖远黄河大桥(图1)为五跨刚构-连续组合梁桥,主跨部分为374 m. 振动测试的测点布置,如图2所示.靖远黄河大桥上、下游两侧共设置42个竖向测点(V1~V42),竖向测试采用垂直向加速度传感器,分7组进行量测,每组有6个可移动测点;纵向和横向的量测采用单侧量测的方法,单侧均布置20个测点(纵向测点L1~L20,横向测点T1~T20),水平向加速度传感器分别沿纵桥向和横桥向布置,纵向测试和横向测试均分为4组进行量测,每组有5个可移动测点.测点10为竖向、横向和纵向三向量测时各组公用的参考点.振动测试的采样频率为102.405 Hz,采样时间为20 min. 图1 靖远黄河大桥 图2 振动测试的测点布置(单位:m)Fig.1 Jingyuan Yellow River Bridge Fig.2 Arrangement of measure points for vibration test (unit: m) 为了衡量单个测点数据识别的模态参数不确定性,以竖向测点16为例,采样时间为20 min,该测点的加速度时程曲线及傅里叶频谱图(0~5 Hz),如图3所示.图3中:av为竖向加速度;Av为振幅;f为固有频率. 以60 s为一个时间段,将竖向测点16的竖向加速度时程分成20组数据,可以识别20组模态参数.利用自助抽样法,假设重复抽样1 000次,计算1 000个自助样本的统计特征值,以样本均值的均值作为该测点的固有频率识别值,以自助样本均值的方差评估参数识别的不确定性.将文中方法与特征系统实现算法(ERA)、有限元模型修正后的计算结果进行对比,竖向测点16前3阶固有频率对比(局部),如表1所示. 由表1及式(13),(15)可知:单测点识别的前3阶固有频率与特征系统实现算法(ERA)及有限元模型修正后的计算结果基本一致;前3阶固有频率的方差分别为0.015 3,0.049 6,0.018 2,自助样本均值的方差分别为0.003 3,0.018 5,0.003 9,测点16的识别结果整体稳定性较好,离散程度较低,第2阶固有频率的方差大于第1阶和第3阶,其不确定性相对较高.由于随机子空间法识别阻尼的精度不高,故阻尼比的识别算法还需进一步研究,此处不考虑阻尼比的不确定性. (a) 加速度时程曲线 (b) 傅里叶频谱图(0~5 Hz)图3 竖向测点16的加速度时程曲线和傅里叶频谱图(0~5 Hz)Fig.3 Acceleration time history curve and Fourier spectrum (0-5 Hz) of vertical measure point 16 表1 竖向测点16前3阶固有频率对比(局部)Tab.1 Comparison among first three natural frequencies of vertical measure point 16 (local) Hz 竖向测点16基于60~120 s,780~840 s及20 min的加速度识别数据得到的稳定图,如图4~6所示.由图4,5可知:基于60~120 s的加速度识别数据仅识别出第1阶和第3阶的固有频率,第2阶固有频率未被识别;基于780~840 s的加速度识别数据可以识别出前3阶固有频率,但第2阶的识别结果的稳定性较差,与方差分析结果一致. 由图4~6可知:采用不同时间段的数据,得到的模态参数识别结果不同;方差可作为识别准确度的评价指标,从而进一步提高模态参数的识别结果. 图4 竖向测点16的稳定图(60~120 s) 图5 竖向测点16的稳定图(780~840 s) Fig.4 Stabilization diagram of vertical Fig.5 Stabilization diagram of vertical measure point 16 (60-120 s) measure point 16 (780-840 s) 图6 竖向测点16稳定图(20 min)Fig.6 Stabilization diagram of vertical measure point 16 (20 min) 对于每个测试组的加速度响应数据,通过SSI-COV算法识别其模态参数,以竖向42个测点的加速度时程数据为例.以7个测试组识别的固有频率值为样本观察值,采用文中方法对多组模态参数识别结果进行不确定性量化,并与ERA、有限元模型修正后的计算结果进行对比.竖向测点16前3阶固有频率对比(整体),如表2所示. 由表2及式(13),(15)可知:前3阶固有频率的方差较小,分别为0.076 1,0.042 9,0.096 5,识别的固有频率值总体上较为稳定,自助样本均值的方差分别为0.021 0,0.009 7,0.020 7;采用自助样本均值的均值作为固有频率识别值,减少了随机误差,与ERA及有限元模型修正后的分析结果对比,三者的识别结果基本一致. 表2 竖向测点16前3阶固有频率对比(整体)Tab.2 Comparison among first three natural frequencies of vertical measure point 16 (whole) Hz 提出一种基于Bootstrap抽样的模态参数识别不确定性量化方法,从整体和局部的角度量化靖远黄河大桥模态参数识别结果的不确定性,得到以下2点结论. 1) 单个测试组识别的前3阶固有频率均值分别为1.526 5,1.788 0,2.306 0;方差分别为0.015 3,0.049 6,0.018 2;不同测试组识别的前3阶固有频率的均值分别为1.553 9,1.720 6,2.165 2;方差分别为0.076 1,0.042 9,0.096 5.这说明识别的固有频率值总体上较为稳定. 2) 样本均值的均值、均值的方差都可以用于评价模态参数识别结果局部,以及整体的大小与变异程度,即均值的方差越小,不确定性越小,识别结果的可信度越高;反之,则说明不确定性越大,波动越大,离散程度越高.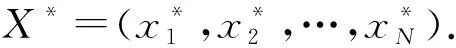
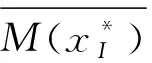

2 工程实例
2.1 工程概况
2.2 模态识别结果的局部不确定性量化



2.3 模态识别结果的整体不确定性量化

3 结论
