基于数学核心素养的一题多解分析

祝 燕

(广东省梅县东山中学 514017)

现在我国对人才的要求是综合化、创新化，如果缺乏对事物的“举一反三”能力，将很难面对今后复杂多类的现实问题，很难适应社会的需要.一题多解是指利用不同的思维方法，对于同一个问题使用两种或者两种以上的方法策略进行分析解答.以下通过具体实例的求解进行阐述.

(1)求动点C的轨迹方程；

(2)假设直线l与动点C所形成的轨迹相切于点P，并与直线x=4相交于一点Q，那么以PQ为直径的圆是否经过x轴上的某定点？若经过，求出该点坐标；若不经过，请说明理由.

(2)方法一设而不求，精准计算.

由题意分析可知，直线l的斜率是存在的，那么可设直线l的方程为：y=kx+m.

依题意，Δ=(8km)2-4(3+4k2)(4m2-12)=0，即3+4k2=m2.

综合以上分析，可知以PQ为直径的圆必过x轴上的定点(1，0).

方法二善用性质结论，减少复杂运算.

将各点坐标代入整理可得(x0-t)·(4-t)+3-3x0=0，即x0(1-t)+t2-4t+3=0.

因为x0是任意取的，所以有1-t=0，t2-4t+3=0同时成立，所以t=1.

故以PQ为直径的圆必过x轴上的定点(1，0).

方法三由特殊到一般，代入验证.

易得到与x轴的交点坐标分别为(1,0)，(3,0).

小结一般情况下，对于圆锥曲线中的定点、定值问题通常有两类处理方法：

(1)参数法：对动点坐标或动直线方程系数，引进相关参数，利用参数表示坐标或系数等，然后依据题意，分析定点、定值成立的条件，得出方程，进而解方程求出答案.

(2)从特殊到一般的推理法：先选择一些特殊点(如坐标轴上的点)或特殊直线(如垂直于x轴或y轴的直线，经过原点的直线等)探究求出满足条件的点坐标或某值，再进一步证明该点或值与相关变量无关，那么即为所要求的定点或定值等.

(1)求椭圆C的标准方程；

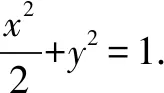
(2)方法一设而不求，精准计算.

(a)若直线的斜率存在，可设直线方程为y=k(x-1)(k≠0)，交点A，B的坐标分别为A(xA，yA)，B(xB，yB).

那么依据题意有：

方法二由特殊到一般，代入验证.

在平时学习、考试碰到的数学问题中，很多通过各个板块知识交汇编制的数学题都具有采用一题多解策略分析求解的可能，具备培养处理数学问题核心素养的价值.通过对此类题目进行一题多解的探究，不仅有助于培养学生的数学思维能力、解题能力、探究能力等，而且可以在探究多种解法的过程中，通过各种解法的相互比较，促进学生积极地、全面地灵活运用所学数学知识处理数学问题，有助于学生进一步理解数学知识、掌握数学方法、提升数学能力、培育数学素养.