一类有关具体函数图象对称中心问题的研究
2020-07-22武增明
武增明
(云南省玉溪第一中学 653100)
高中数学学习过程中,我们知道,一些具体函数图象是有对称中心的,常见的具体函数有常数函数、一次函数、三次函数、反比例函数、正弦函数、余弦函数、正切函数.笔者在这里与读者一起要研究的主要是,一类由上述函数构成的具体函数且函数图象具有对称中心的有关问题.同时,温馨提醒同学们要有函数图象的对称中心意识,也供同仁们在教学中作参考,希望能起到抛砖引玉的作用.
一、重要性质

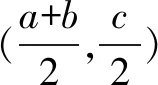
性质3若函数f(x)是奇函数,则函数g(x)=f(x-a)+b的图象关于点(a,b)对称.
二、有关一般函数图象的对称中心问题
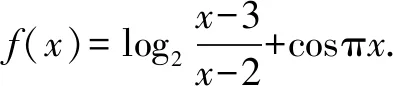
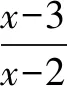


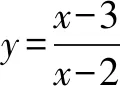
又-1≤cosπx≤1,于是,当x>4时,-2 因为f(β)=-10,从而β∈(3,4)且是唯一的. 同理,由函数y=(x-2)(x-3)及y=-sinπx的图象,知当x∈(1,2)时,f′(x)>0,所以函数f(x)在(1,2)上单调递增,且f(1)=0. 又-1≤cosπx≤1,于是,当x<1时,-1 因为f(α)=10,从而α∈(1,2)且是唯一的. 所以函数f(x)的图象关于点(0,2)对称,从而f(x)max+f(x)min=4,即m+n=4. (2)本题先将原函数进行化简,然后利用函数y=f(x)的图象关于点(0,2)对称,求得m+n=4,并不需要分别求出m与n的值.事实上,要分别求出m与n的值是非常困难的,甚至几乎求不出来.(3)若没有想到函数y=f(x)的图象是否关于点对称,进而用相关性质解答,而尝试用导数的知识分别去求m与n的具体数值,就会深陷泥沼,无法自拔了. 1.问题的提出 2.问题的探究 f(x)=3+g[x+(a+2)],当a+2=0,即a=-2时,将函数g(x)的图象向上平移3个单位,得到函数f(x)的图象,其图象关于点(0,3)对称. 当a+2>0,即a>-2时,将函数g(x)的图象向左平移a+2个单位,再向上平移3个单位,得到函数f(x)的图象,其图象关于点(-a-2,3)对称. 当a+2<0,即a<-2时,同理可得函数f(x)的图象关于点(a+2,3)对称. 3.一点反思 凡是同学们提出的问题是合理的,我们都要热情地、耐心地、认真地、千方百计地帮助和引导,鼓励同学们大胆地用合作探究的方式去加以解决. 例3 (2016年全国数学联赛山东省预赛试题)设α,β分别满足方程α3-3α2+5α-4=0,β3-3β2+5β-2=0,则α+β=____. 解析观察题目条件α3-3α2+5α-4=0,β3-3β2+5β-2=0,想到设f(x)=x3-3x2+5x,则f(α)=4,f(β)=2. 因为三次函数f(x)=x3-3x2+5x的图象的对称中心为(1,3),f′(x)=3x2-6x+5>0对x∈R恒成立,故f(x)在R上单调递增. 评注(1)若没有想到三次函数的图象的对称中心,则很难求解.(2)要求出α,β的值,是很困难的. 例4 (2012年高考四川卷·文12)设函数f(x)=(x-3)3+x-1,{an}是公差不为0的等差数列,f(a1)+f(a2)+…+f(a7)=14,则a1+a2+…+a7=( ). A. 0 B. 7 C. 14 D. 21 解f(x)=(x-3)3+x-1=x3-9x2+28x-28,f(x)是关于点(3,2)成中心对称的增函数. ∵f(a1)+f(a2)+…+f(a7)=14, ∴f(a4)=2, ∴(a4-3)3+a4-1=2, ∴a4=3. ∵{an}是等差数列, ∴a1+a2+…+a7=7a4=21,故选D. 评注此题解法较多,只有利用三次函数f(x)=x3-9x2+28x-28是关于点(3,2)成中心对称的增函数来解答最简捷. 下面给出一组变式题目,供同学们训练,也供同仁们在教学中作参考. 1.已知函数f(x)=x3-9x2+29x-30,实数m,n满足f(m)=-12,f(n)=18,则m+n=____. 2.已知实数x,y满足x3+5x-3=3x2+1,y3+5y-1=3y2+1,则x+y=____. A. (-4,6) B. (-2,3) C. (-4,3) D. (-2,6) A. (2,3) B. (2,0) C. (3,2) D. (3,0) 参考答案为:1. 6; 2. 2; 3. B; 4. A; 5. 5; 6. 4.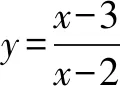


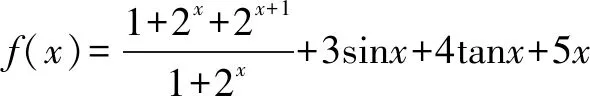
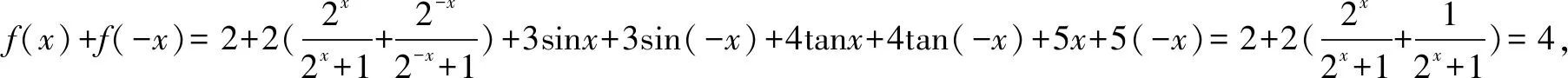

三、一类分式型函数图象的对称中心问题
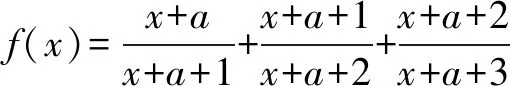
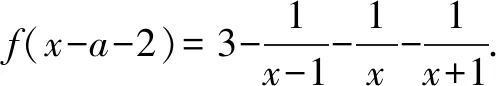
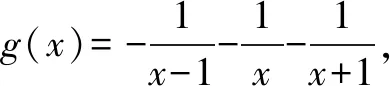
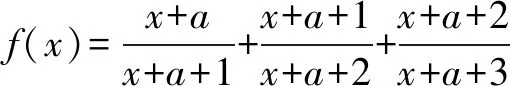
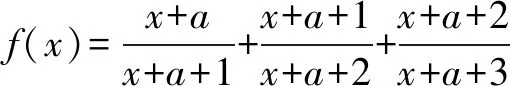
四、有关三次函数图象的对称中心问题
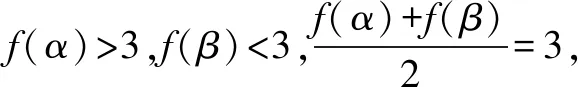

五、一组变式题