例谈平面向量的数量积的应用

刘立强

(甘肃省康县第一中学 746500)

平面向量的数量积是平面向量的重要内容，也是高考命题的一个热点，主要考查平面向量数量积的运算、几何意义、模与夹角、垂直等问题.下面举例说明平面向量的数量积常见的几种应用，供参考.

一、求向量的长度(模)

例1已知向量a、b、c两两所成的角相等，均为120°，且|a|=2，|b|=3，|c|=1，求向量a+b+c的长度.

点评根据题意先求|a+b+c|2的值是求|a+b+c|的关键.

二、求两向量夹角

例2已知a，b是两个非零向量，且|a|=|b|=|a-b|，求a与a+b的夹角.

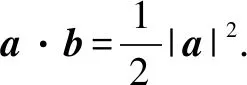
三、求解两向量的垂直问题

例3已知|a|=5，|b|=4，且a与b的夹角为60°，则当k为何值时，向量ka-b与a+2b垂直？

分析利用向量垂直的充要条件(ka-b)·(a+2b)=0及数量积的运算性质展开，列出关于k的方程即可.

点评解决向量垂直问题常用向量数量积的性质a⊥b⟺a·b=0，这是一个重要性质，它把垂直问题转化为代数计算问题.

四、判断三角形的形状

分析由已知条件可根据角来判断三角形的形状.

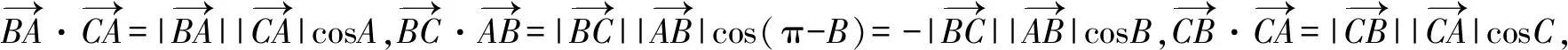
点评根据向量数量积的有关知识判断平面图形的形状，关键是由已知条件建立数量积、向量的长度、向量的夹角等之间的关系.

五、求参数的取值范围

分析根据向量a+λb与λa+b的夹角是锐角时，则有(a+λb)·(λa+b)>0且(a+λb)与(λa+b)不共线，列出关于λ的不等式即可.

六、证明平面几何题