对数公式大汇集及其证明、应用

甘志国

(北京市丰台二中 100071)

一、对数公式大汇集及其证明

(1)对数的定义：ab=N⟺logaN=b.

(2)对数恒等式：logaab=b；alogaN=N(由定义中的两个式子等量代换即得).

(4)对数的运算性质——积、商、幂、方根的对数：

①loga(MN)=logaM+logaN；

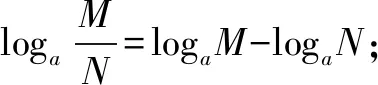
③logaMn=nlogaM；

证明①由对数的定义知，即证

alogaM+logaN=MN.

这由第二个对数恒等式易证：

alogaM+logaN=alogaM·alogaN=MN.

②即证

这由①立得.

③由对数的定义知，即证

anlogaM=Mn.

证明如下：

anlogaM=(alogaM)n=Mn

④由③立得.

证明即证logxN=logxalogxN，也即证

xlogxalogaN=N.

证明如下：

xlogxalogaN=(xlogxa)logaN=alogaN=N.

(7)对数的同次幂公式：loganNn=logaN.

(9)对数的循环公式：loga1a2·loga2a3·…·logan-1an=loga1an.

(10)对数的重排公式：loga1b1·loga2b2·…·loganbn=1(其中a1,a2,…,an与b1,b2,…,bn这两组数仅仅次序不同).

(6)～(10)均可由(5)证得，下面证明(10)：

(11)幂的换底公式：ab=xblogxa(由第二个对数恒等式易证).

注以上公式均在两边有意义时才能成立.

对数中有很多趣题，其中以对数换底公式的应用最多，比如后文例4的证法2.

二、对数公式的应用

(6)lg2lg50+lg5lg20-2lg2lg5；

(9)(log25+log40.2)(log52+log250.5)；

解(1)a1+logab=a1·alogab=ab.

(6)lg2lg50+lg5lg20-2lg2lg5=lg2(lg5+1)+lg5(lg2+1)-2lg2ln5=lg2+lg5=1.

例2(1)若log147=a,log145=b，则log3528=____(用a,b表示)；

(2)若log83=a,log35=b，则lg5=____(用a,b表示).

(2)由题设，可得

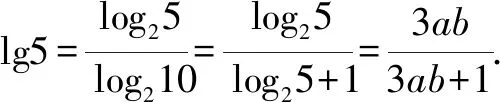
例3(原创题)(1)若log303=a,log305=b，则log308=____(用a,b表示)；

(2)若log712=a,log1224=b，则log54168=____(用a,b表示)；

(3)若α=log1218,β=log2454，则αβ+5(α-β)=____.

解(1)3-3a-3b.由题设，可得

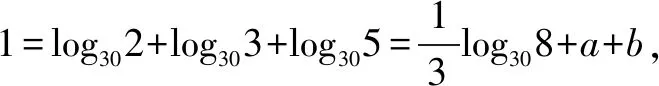
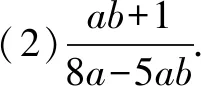
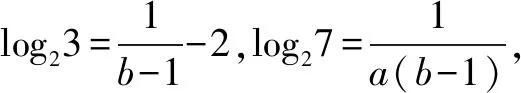
(3)1.由题设，可得

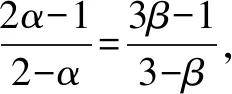
αβ+5(α-β)=1.

例4求证algb=blga.

证法1只需证lgalgb=lgblga.

由幂的对数运算法则知，即证lgblga=lgalgb.

而此式显然成立，所以要证结论成立.

证法2只需证a=blga/lgb.

由对数的换底公式知，即证a=blogba.

这由对数恒等式，立知成立.所以要证结论成立.

还可把本题的结论推广为alogxb=blogxa.

例5(原创题)甲、乙二人同解一道数学题：先求某个三位正整数的以2为底的对数，再把所得的结果减去另一个正整数b，最后求所得的差与b的商.甲在解题时把“以2为底”看成了“以3为底”而后进行了正确的计算，乙计算出了正确的结果.当两人核对自己的计算结果时，发现他们所得的结果互为倒数.根据这些信息，请求出这道题的正确答案.

解设这道题中的三位正整数是a，由题设，可得

(log2a-b)(log3a-b)=b2,

b(log2a+log3a)=log2alog3a,

b(loga2+loga3)=1,

bloga6=1,

a=6b(a,b∈N*,100≤a≤999).

再由63=216,64=1296，可得a=63=216,b=3，所以所求答案是