也谈一道竞赛题的解法与推广

贵州省毕节梁才学校 (551700) 翁文建

题目(2018年全国高中数学联赛天津市预赛题)已知实数x,y满足x2+y2=20，求p=xy+8x+y的最大值.

本题目的一般解法是消元法和换元法化为一元方程或一元函数求值域，即下面的分析1—分析3.

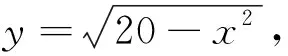
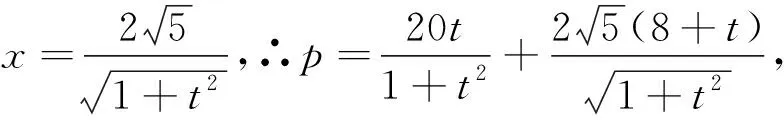
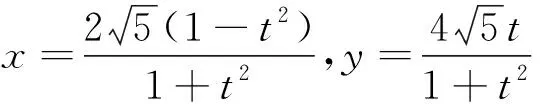
题目的另一个不易想到的方法是通过放缩使目标函数与约束条件满足不等式xy+8x+y≤λ(x2+y2)+μ(λ>0)，且等号成立，达到整体消元求最大值.而用什么不等式放缩是很难想到的，本文用待定系数给出几种解法，并对该题做部分推广.

由于xy+8x+y≤λ(x2+y2)+μ⟺λx2+λy2-xy-8x-y+μ≥0是可解二次不等式(方程)，是可用基本的求根公式或配方法化为f2(x,y)+kg2(x,y)≥0(k>0)的.

解法1：令xy+8x+y≤λ(x2+y2)+μ(λ>0)，即λx2+λy2-xy-8x-y+μ≥0，即λx2-(y+8)x+λy2-y+μ≥0，对应方程根

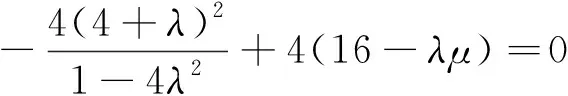
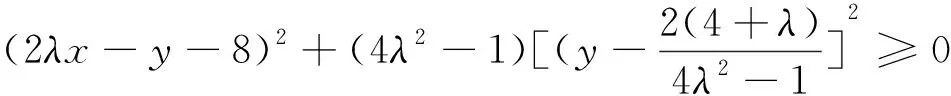
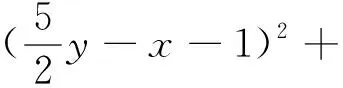
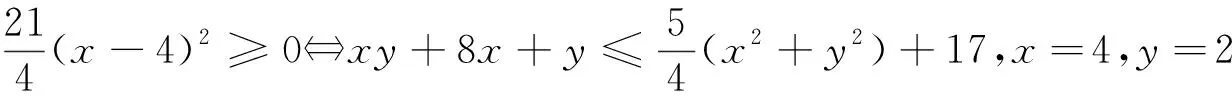
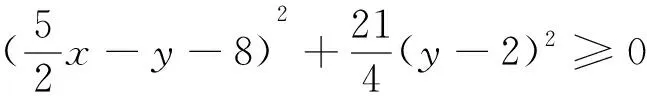
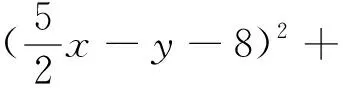
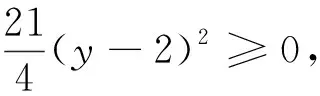
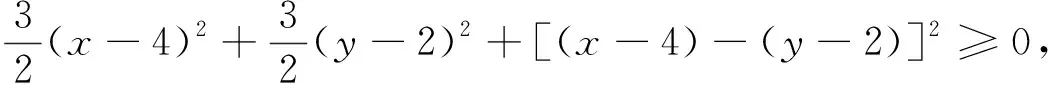
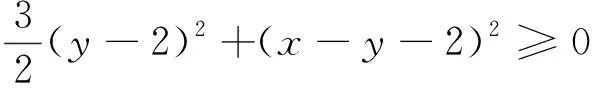
解法4：在解法3中，由25(x-4)2+25(y-2)2-20(x-4)(y-2)≥0得5(x-4)2+5(y-2)2-4(x-4)(y-2)≥0，即(x-4)2+4(y-2)2+4(x-4)2+(y-2)2-4(x-4)(y-2)≥0，即(x-4)2+4(y-2)2+[2(x-4)-(y-2)]2≥0，即(x-4)2+4(y-2)2+(2x-y-6)2≥0，

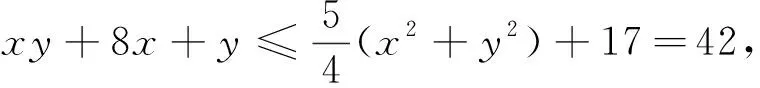
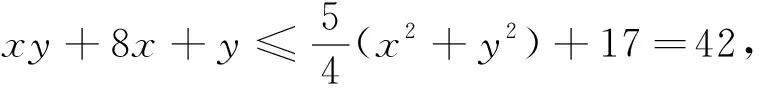
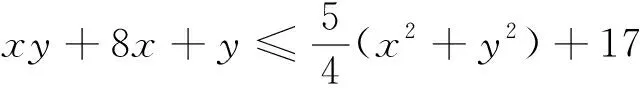
上述待定系数法可推广到三元上，只是运算太繁，只举一略去繁琐运算的例.

例已知实数x,y,z满足x2+y2+z2=14，求p=xy+yz+zx+3x+12y+21z的最大值(文[1]的问题9).

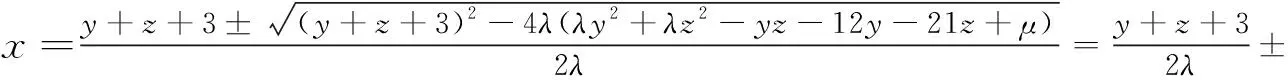
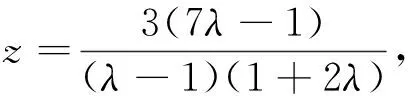
总之，把问题转化为特殊的完整二元二次不等式Ax2+Ay2+Bxy+Dx+Ey+F≥0或方程问题,用基本的求根公式解决.