一类刚柔协作混联机器人机构的绳索数量和位置分布研究

2020-07-21张俊宝侯红娟崔国华

工程设计学报 2020年3期

张俊宝，侯红娟，崔国华,2，刘健

（1.河北工程大学机械与装备工程学院，河北邯郸056038；2.上海工程技术大学智能机器人研发中心，上海201620；3.复旦大学工程与应用技术研究院，上海200433）

随着抛光、打磨工艺自动化水平的不断提高，并、混联机器人机构广泛应用于抛光、打磨等工艺，其中3UPS-UP机器人机构应用较为广泛，许多专家学者都对该机构进行了研究。例如：天津大学的王友渔对3UPS-UP机器人机构的刚度进行了解析建模分析［1］；北京工业大学的卿建喜、李剑锋等对冗余驱动Tricept并联机构进行了驱动优化和奇异性分析［2-3］；天津大学的王玉茹等对Tricept并联机器人的运动学理论进行了论述［4］；河北工程大学的刘健对刚柔协作搅拌摩擦焊机器人机构进行了设计与性能研究［5］。笔者拟基于3CD-3UPS-UP刚柔协作混联机器人机构，通过改变其绳索的数量及位置分布，得到3种不同的刚柔协作混联机器人机构，并对它们进行运动学分析，求取量纲统一速度雅克比矩阵；同时，分析3种刚柔协作混联机器人机构在不同工作高度下的各项性能指标并进行对比。

1 刚柔协作混联机器人机构的运动学模型

刚柔协作混联机器人机构由3UPS-UP刚性部分和绳索部分组成。如图1所示，Ai（i=1，2，3）表示刚性部分动平台的铰点，Bi（i=1，2，3）表示刚性部分定平台的铰点，Cj/Dj/Ej（j=1，2，3/j=1，2，3，4/j=1，2，3，4，5）表示绳索部分定平台的铰点，其中刚性部分动、定平台的铰点呈正三角形分布，绳索部分定平台的铰点呈正三角形、正方形、正五边形分布。分别以刚柔协作混联机器人机构各平台的几何中心为原点构建基坐标系O-x′y′z′、局部坐标系A-uvw和全局坐标系B-xyz。将抛光、打磨设备放置在刚柔协作混联机器人机构动平台几何中心A处。

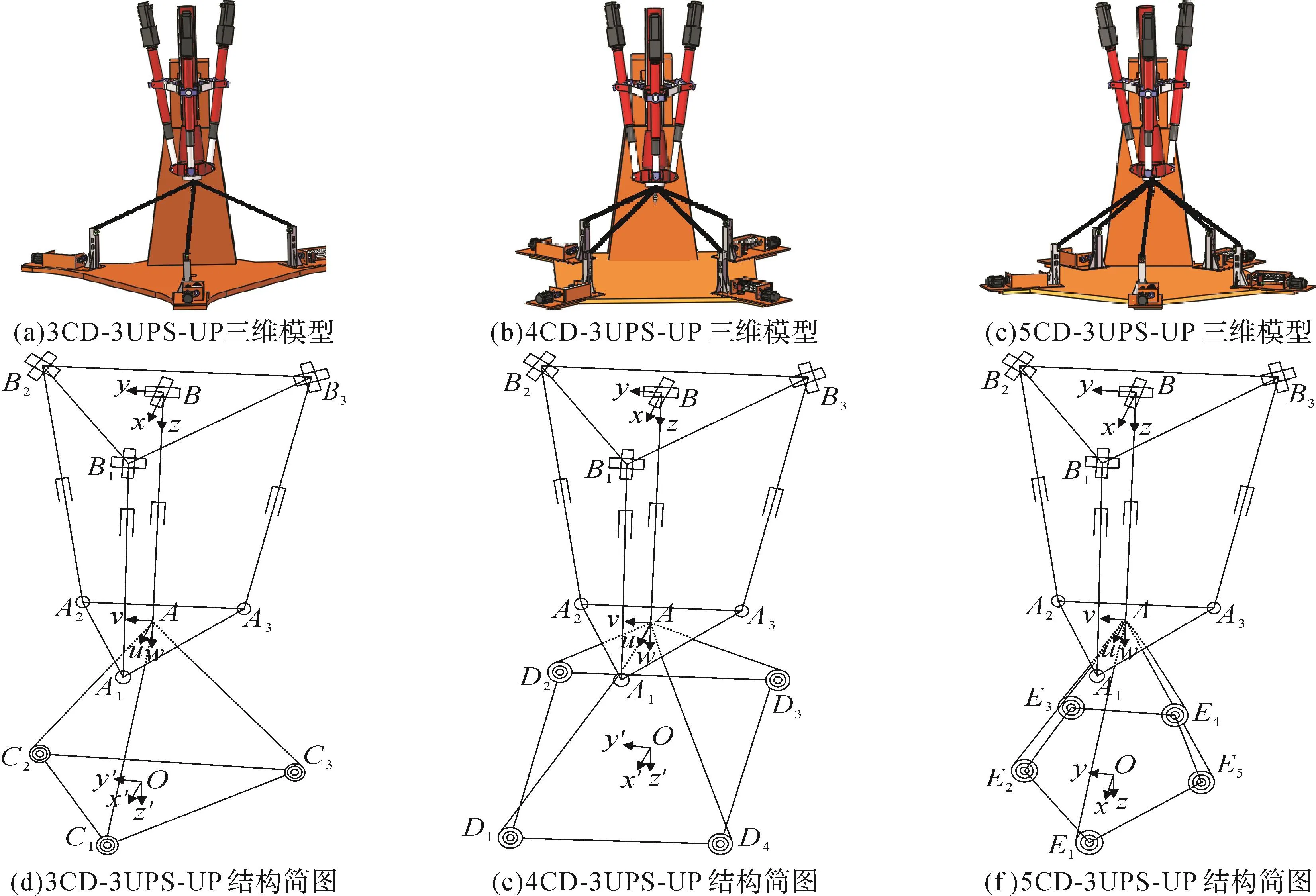
图1 3种刚柔协作混联机器人机构的模型Fig.1 Models of three kinds of rigid-flexible cooperative hybrid robot mechanisms

2 刚柔协作混联机器人机构的位置逆解

2.1 刚性部分的位置逆解

令△B1B2B3和△A1A2A3的外接圆半径分别为b和a，则铰点Ai在局部坐标系A-uvw下的位置矢量为：

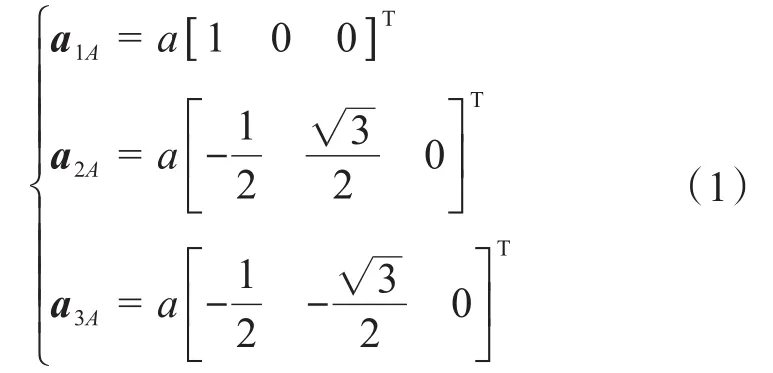
铰点Bi在全局坐标系B-xyz下的位置矢量为：

设局部坐标系A-uvw到全局坐标系B-xyz的旋转矩阵为R，则铰点Ai在全局坐标系B-xyz下的位置矢量ai=RaiA。令点A在全局坐标系B-xyz下的位置矢量r=[xyz]T，根据封闭矢量法［6-7］可得3UPS-UP刚性部分的闭环矢量方程为：

式中：qi——支链i的长度；

qi——支链i的单位方向向量。

由此可得3UPS-UP刚性部分的位置逆解为：

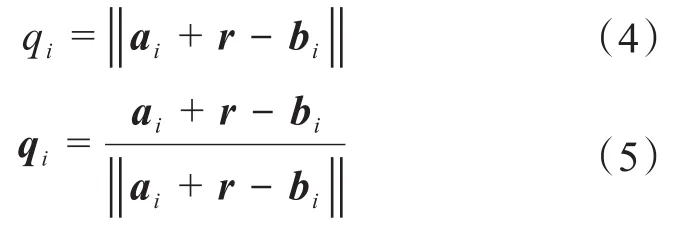
2.2 绳索部分的位置逆解

令3种刚柔协作混联机器人机构绳索部分定平台的外接圆半径为n，则铰点Cj/Dj/Ej在基坐标系O-x'y'z'下的位置矢量分别为：

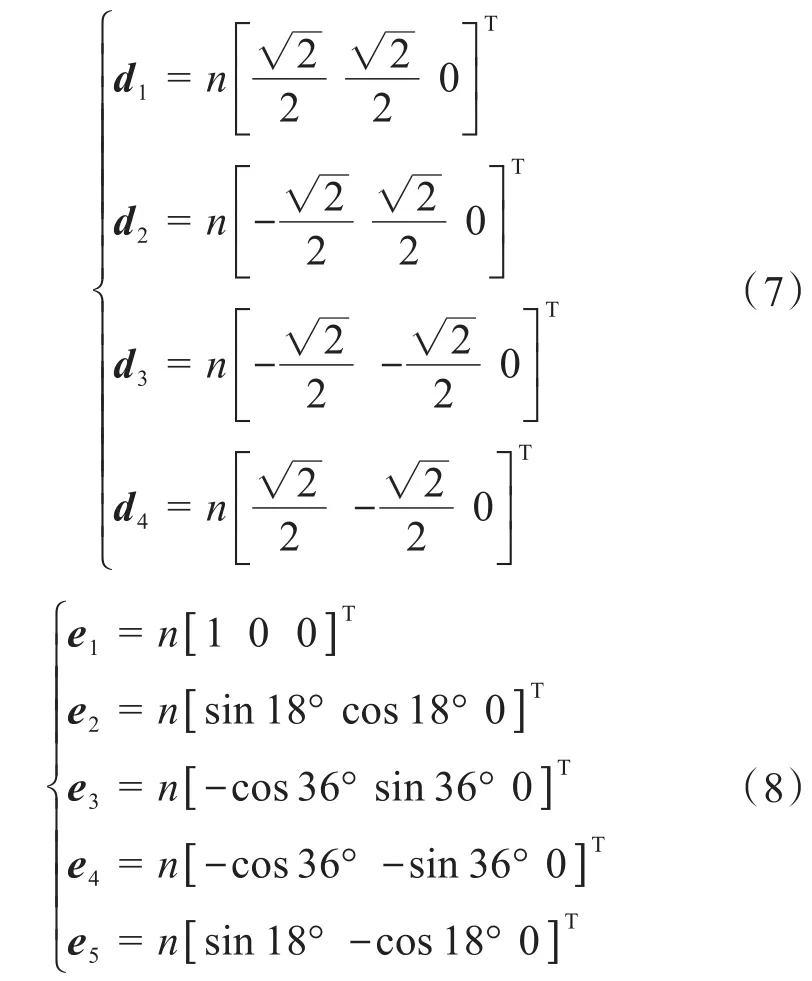
令点A在基坐标系O-x′y′z′下的位置矢量分别为：

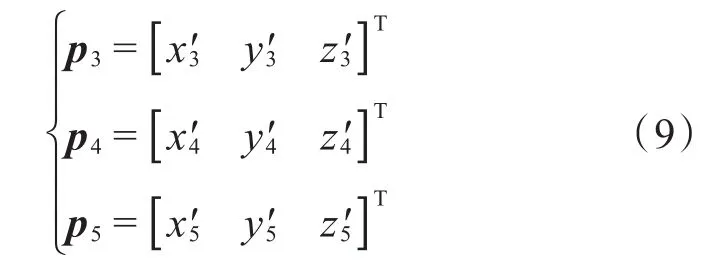
根据封闭矢量法，可得绳索数量分别为3，4，5时绳索部分的闭环矢量方程为：

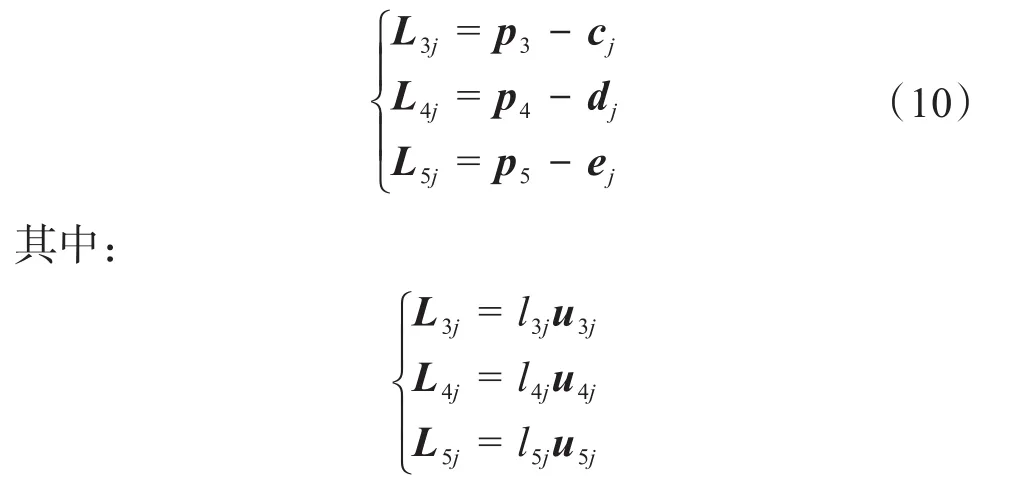
式中：l3j、l4j、l5j——绳索数量分别为3，4，5时绳索j的长度；

u3j、u4j、u5j——绳索数量分别为3，4，5时绳索j的单位方向向量。

由此可得绳索数量分别为3，4，5时绳索部分的位置逆解为：

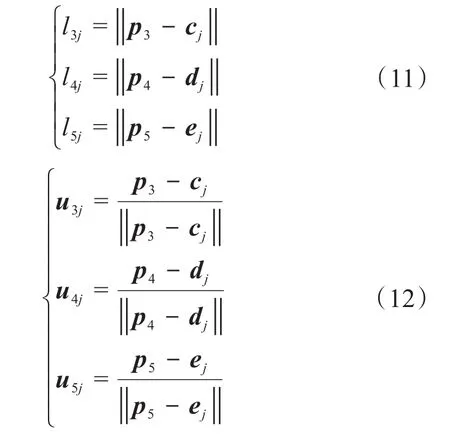
3 刚柔协作混联机器人机构的量纲统一速度雅可比矩阵

刚柔协作混联机器人机构可拆分为3UPS、UP支链及绳索三部分，分别求各部分的速度雅可比矩阵，进而求得其量纲统一速度雅可比矩阵。为方便表示，此节的公式中用s表示sin，用c表示cos。

3.1 速度雅克比矩阵求解

3.1.1 3UPS的速度雅可比矩阵

对式（3）求导［8］可得：

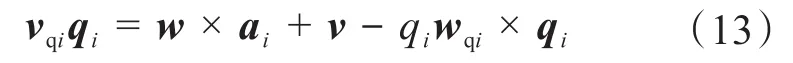
式中：w——动平台的角速度；

v——点A的线速度；

wqi——支链i的角速度；

vqi——支链i的移动副的移动速度。

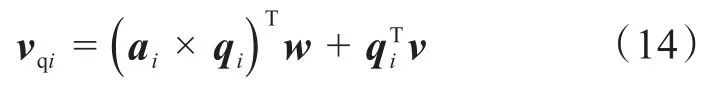
式（14）的矩阵形式为：

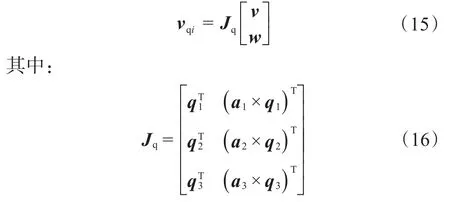
式中：Jq——3UPS的速度雅可比矩阵。

3.1.2 UP支链的速度雅可比矩阵

构建UP支链的D-H坐标系，如图2所示。UP支链的结构参数如表1所示，表中：θg为连杆关节角度，dg为连杆偏距，φg为连杆长度，αg为连杆转角。可将UP支链中的虎克铰U看成2个转动副R，则UP支链可看作R-R-P链，θ1和θ2为2个转动副R的转角，d3为移动副P的位移。

UP支链各连杆坐标系之间的变换矩阵为：

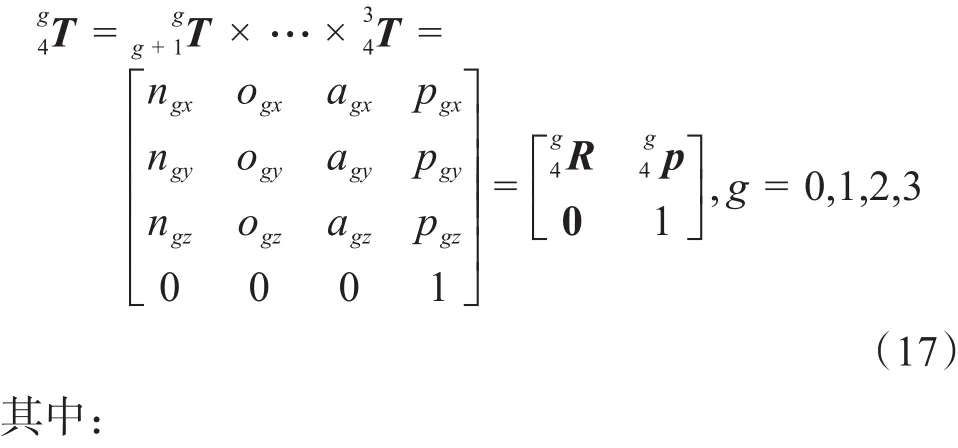
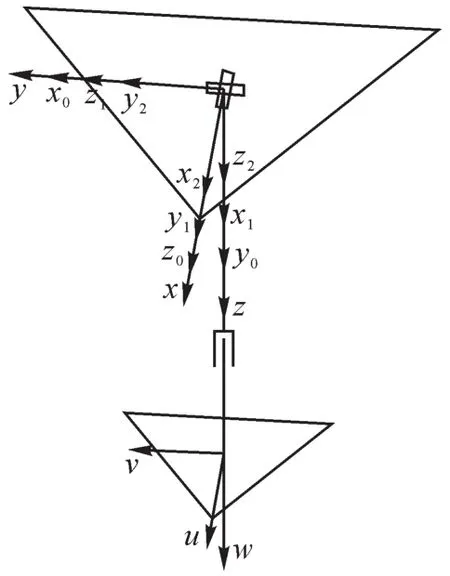
图2 UP支链的D-H坐标系Fig.2 D-H coordinate system of UP branch chain

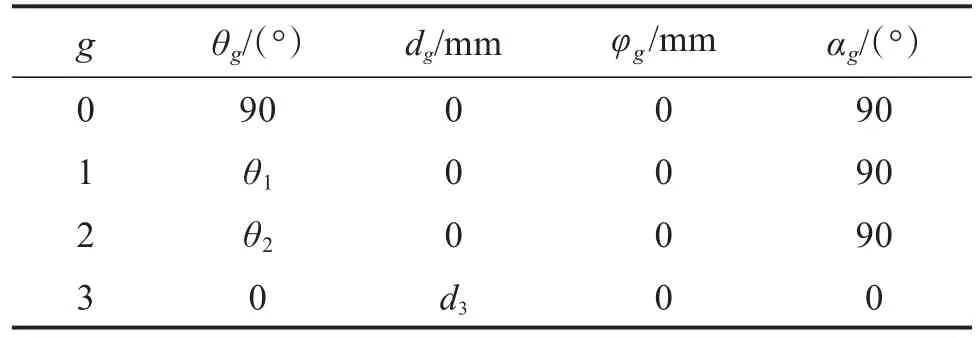
表1 UP支链的结构参数Table 1 Structure parameters of UP branch chain

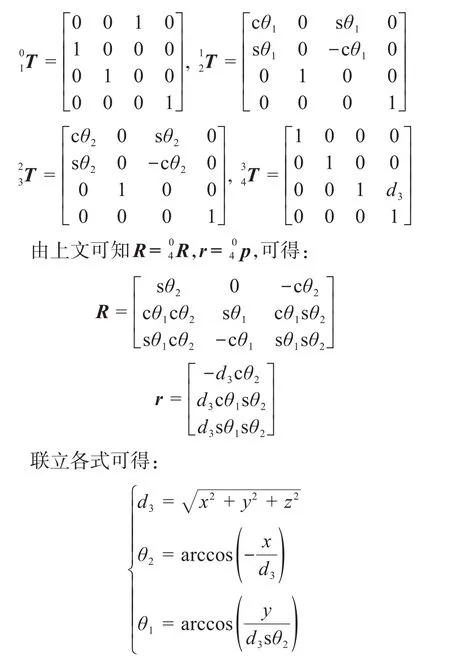
由于关节0不转动，由微分变换法［9］得UP支链的速度雅克比矩阵为：

3.1.3 绳索部分的速度雅可比矩阵

对式（10）求导，可得绳索数量为3，4，5时点A的线速度分别为：

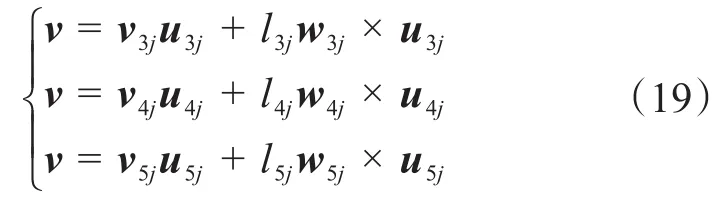
式中：v3j、v4j、v5j——绳索数量分别为3，4，5时绳索j的伸缩速度；

w3j、w4j、w5j——绳索数量分别为3，4，5时绳索j的角速度。

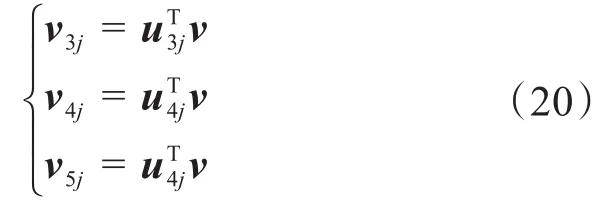
联立各式可得：

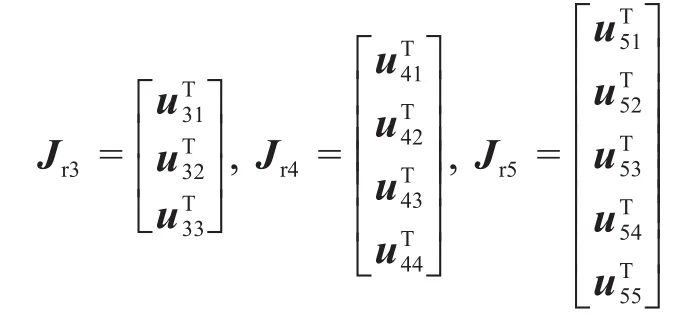
式中：Jr3、Jr4、Jr5——绳索数量为3，4，5时绳索部分的速度雅可比矩阵。

3.2 量纲统一速度雅可比矩阵求解

3.2.1 刚性部分的量纲统一速度雅克比矩阵

令Jp的前3行为Jp1，则可得：

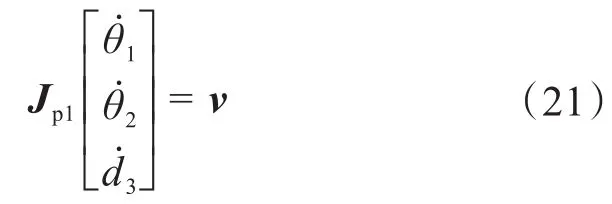
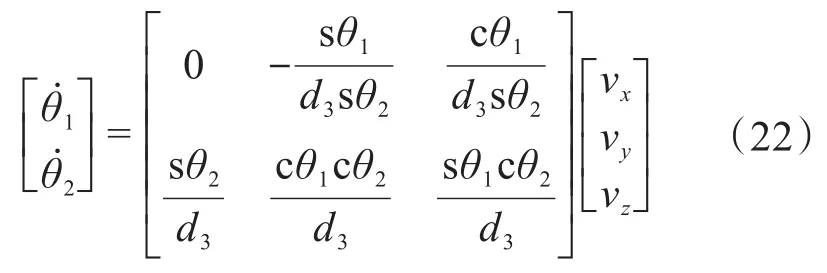
基于式（18）的后3行，同理可得：

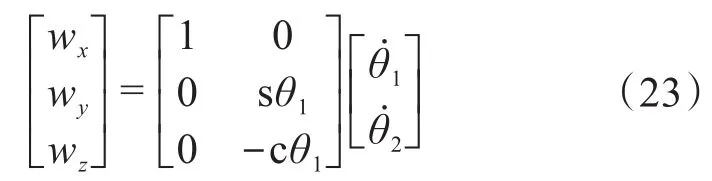
联立式（22）和式（23）可得：

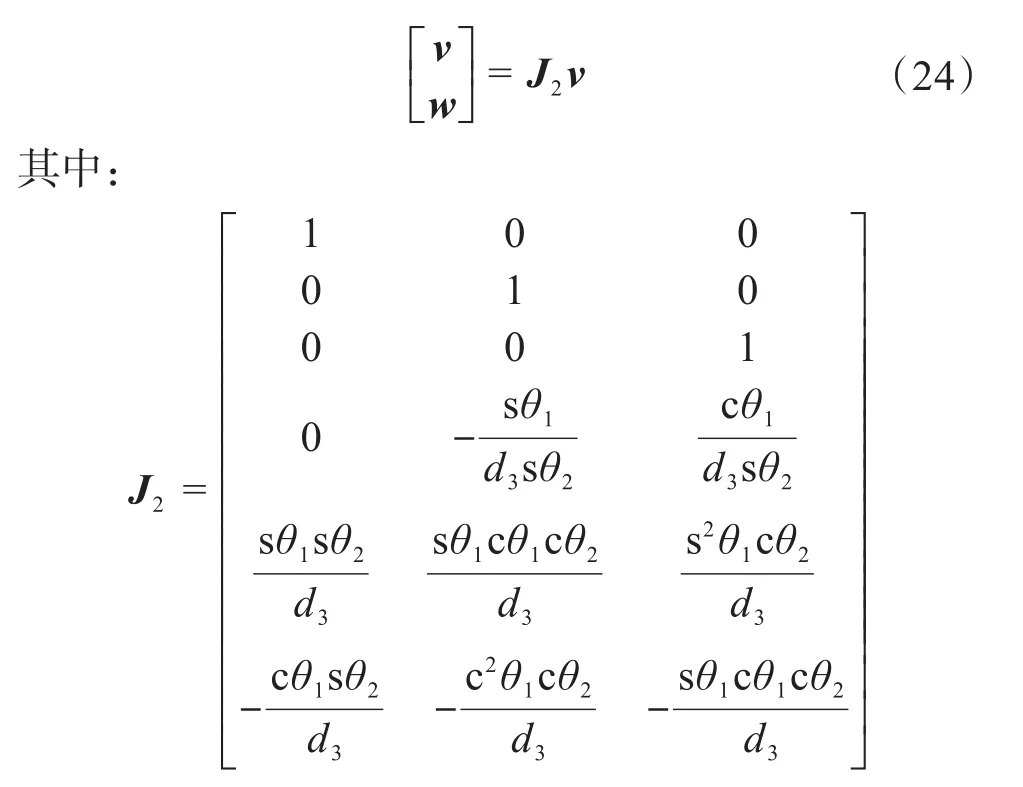
联立式（15）、式（16）和式（24）可得刚柔协作混联机器人机构刚性部分的量纲统一速度雅克比矩阵为：

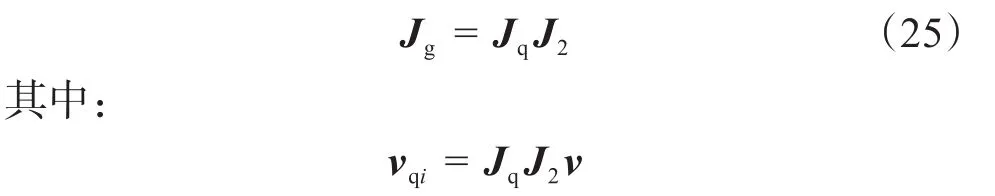
3.2.2 机构的量纲统一速度雅克比矩阵

设T为基坐标系O-x'y'z'到全局坐标系B-xyz的旋转矩阵，令：

式中：Jgr3、Jgr4、Jgr5——绳索数量为3，4，5时刚柔协作混联机器人机构的量纲统一速度雅可比矩阵。

4 刚柔协作混联机器人机构的性能分析

4.1 工作空间

刚柔协作混联机器人机构的工作空间［10-12］受刚性部分支链的长度和运动副转角的约束。刚柔协作混联机器人机构的结构参数如表2所示，其中：h为2个定平台之间的距离，qmin为UPS支链的最小伸缩长度，r为UPS支链最大伸缩长度和最小伸缩长度的比值，β1为虎克铰的最大转角，β2为球铰的最大转角。

以抛光、打磨设备的放置点A为参考点，通过MATLAB软件编程计算得到不考虑绳索部分时刚柔协作混联机器人机构的工作空间，如图3所示。

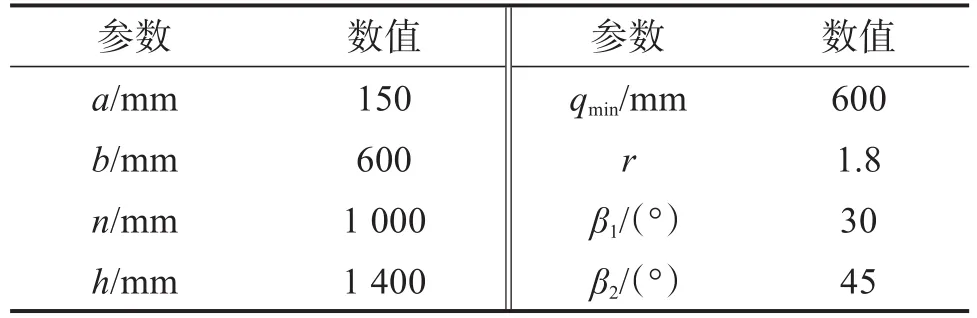
表2 刚柔协作混联机器人机构的结构参数Table 2 Structural parameters of rigid-flexible coopera-tive hybrid robot mechanism

图3 不考虑绳索部分时刚柔协作混联机器人机构的工作空间Fig.3 Workspace of rigid-flexible cooperative hybrid robot mechanism without considering rope part

从图3可以看出，该刚柔协作混联机器人机构的工作空间连续且没有空洞，说明在该工作空间内抛光、打磨运动的连续性较好。

4.2 刚度

通过建立刚度矩阵［13-14］来对刚柔协作混联机器人机构的刚度进行表征。

式中：J——刚柔协作混联机器人机构的量纲统一速度雅克比矩阵，即上文的Jgr3、Jgr4和Jgr5；

KJ——刚柔协作混联机器人机构的刚度矩阵，KJ=diag[q1q2…qm]，其中qm为第m个驱动副的关节刚度。

以刚度矩阵的对角线数值之和LSI为刚柔协作混联机器人机构的刚度指标：LSI越大表明该机构在工作时抵抗变形的能力越强，精度越高。设刚柔协作混联机器人机构刚性部分的刚度Gg=1000N/mm，绳索部分的刚度Gr=500N/mm，通过计算得到不同刚柔协作混联机器人机构（绳索的数量和位置分布不同）的刚度，如图4所示。

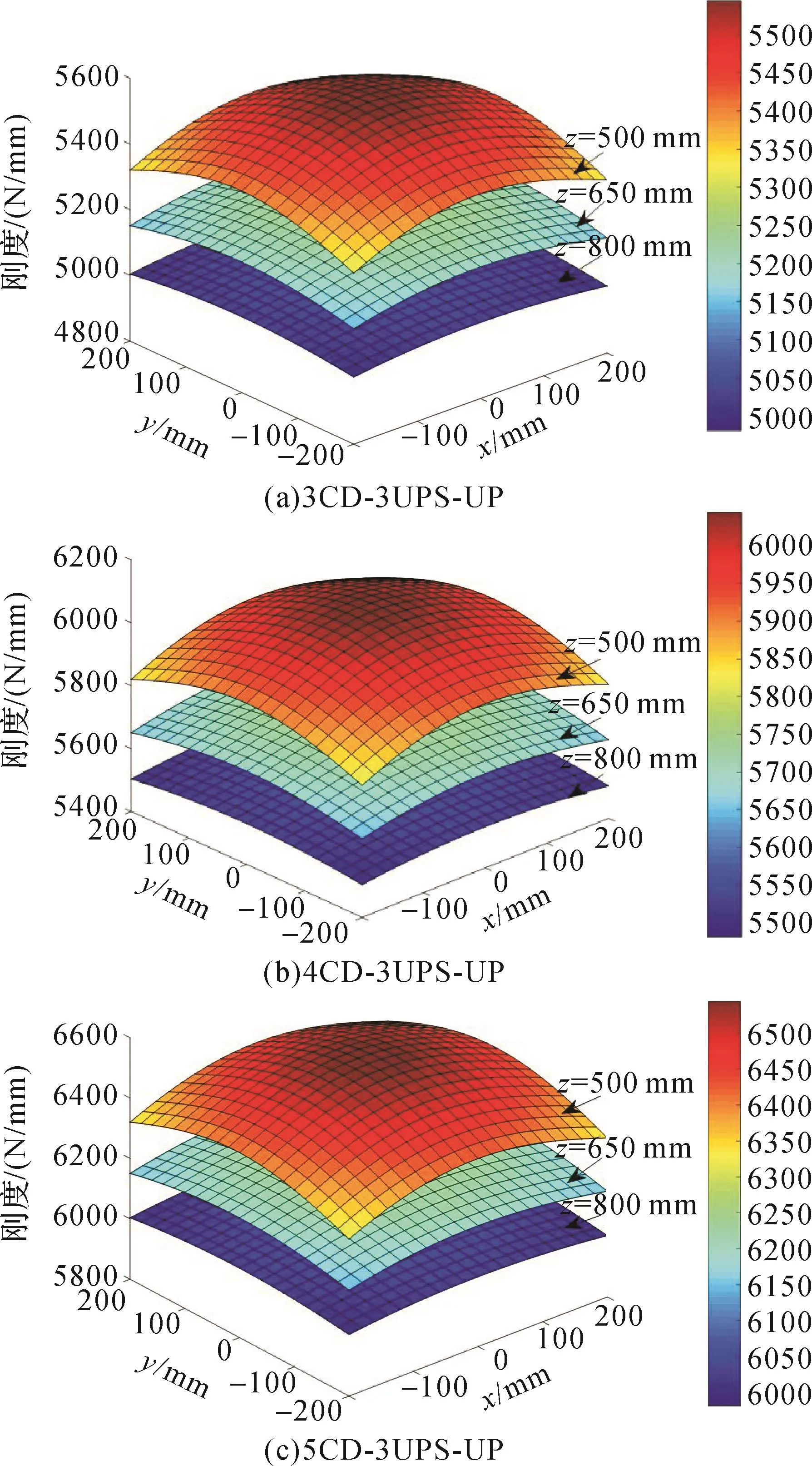
图4 不同刚柔协作混联机器人机构的刚度对比Fig.4 Comparison of stiffness of different rigid-flexible co-operative hybrid robot mechanisms

由图4可知：不同刚柔协作混联机器人机构的刚度均随工作高度z的增大而减小；不同工作高度z下，不同刚柔协作混联机器人机构的最大刚度均在x=0 mm，y=0 mm处出现，最小刚度均在机构所能到达的边缘处出现；随着绳索数量的增加，刚柔协作混联机器人机构的刚度有所增大，更适用于抛光、打磨等工艺。

4.3 全域刚度

刚柔协作混联机器人机构的全域刚度可表示为［15-16］：

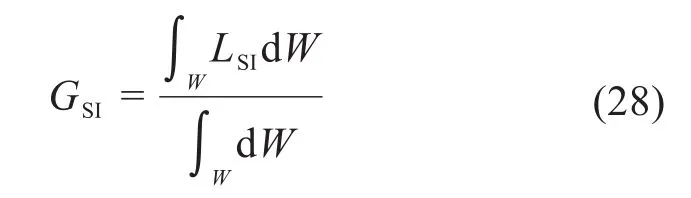
式中：W——刚柔协作混联机器人机构的工作空间。

通过计算可知，3CD-3UPS-UP的全域刚度GSI3=5127.2，4CD-3UPS-UP 的全域刚度GSI4=5627.2，5CD-3UPS-UP的全域刚度GSI5=6127.2。对比可知：绳索的数量和位置分布不同时刚柔协作混联机器人机构的全域刚度不同；随着绳索数量的增加，刚柔协作混联机器人机构的全域刚度增大，更适用于抛光、打磨等工艺。

4.4 灵巧性

将量纲统一速度雅克比矩阵条件数的倒数作为灵巧性的度量［17-20］，即灵巧度，可表示为：

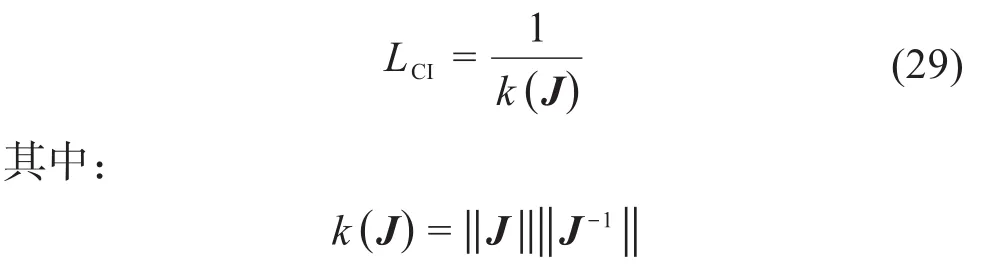
式中：k(J)——量纲统一速度雅克比矩阵的条件数。

力雅克比矩阵与量纲统一速度雅克比矩阵之间的关系为：

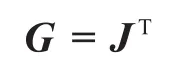
式中：G——力雅克比矩阵。

则有：

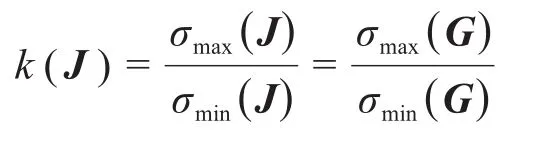
式中：σ(J)——量纲统一速度雅克比矩阵的奇异值；

σ(G)——力雅克比矩阵的奇异值。

灵巧度越接近1表明刚柔协作混联机器人机构的运动传递性能越佳。不同刚柔协作混联机器人机构的灵巧度如图5所示。

由图5可知：不同刚柔协作混联机器人机构的灵巧度均随工作高度z的增大而减小；不同工作高度z下，不同刚柔协作混联机器人机构的最大灵巧度均在x=0 mm，y=0 mm处出现，最小灵巧度均在机构所能到达的边缘处出现；随着绳索数量的增加，刚柔协作混联机器人机构在x=0 mm，y=0 mm附近的灵巧度稍有减小，其余部分灵巧度有所增大。

4.5 全域灵巧性

刚柔协作混联机器人机构的全域灵巧度可表示为［21］：

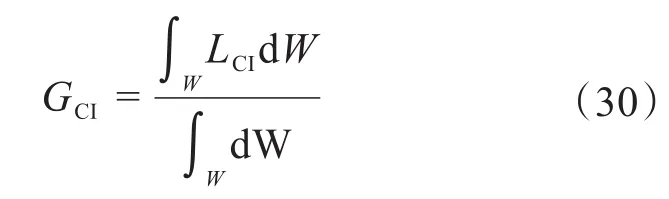
通过计算可得，3CD-3UPS-UP的全域灵巧度GCI3=0.7117，4CD-3UPS-UP的全域灵巧度GCI4=0.7722，5CD-3UPS-UP的全域灵巧度GCI5=0.8001。对比可知：绳索的数量和位置分布不同时刚柔协作混联机器人机构的全域灵巧性不同；随着绳索数量的增加，刚柔协作混联机器人机构的全域灵巧性增强，更适用于抛光、打磨等工艺。

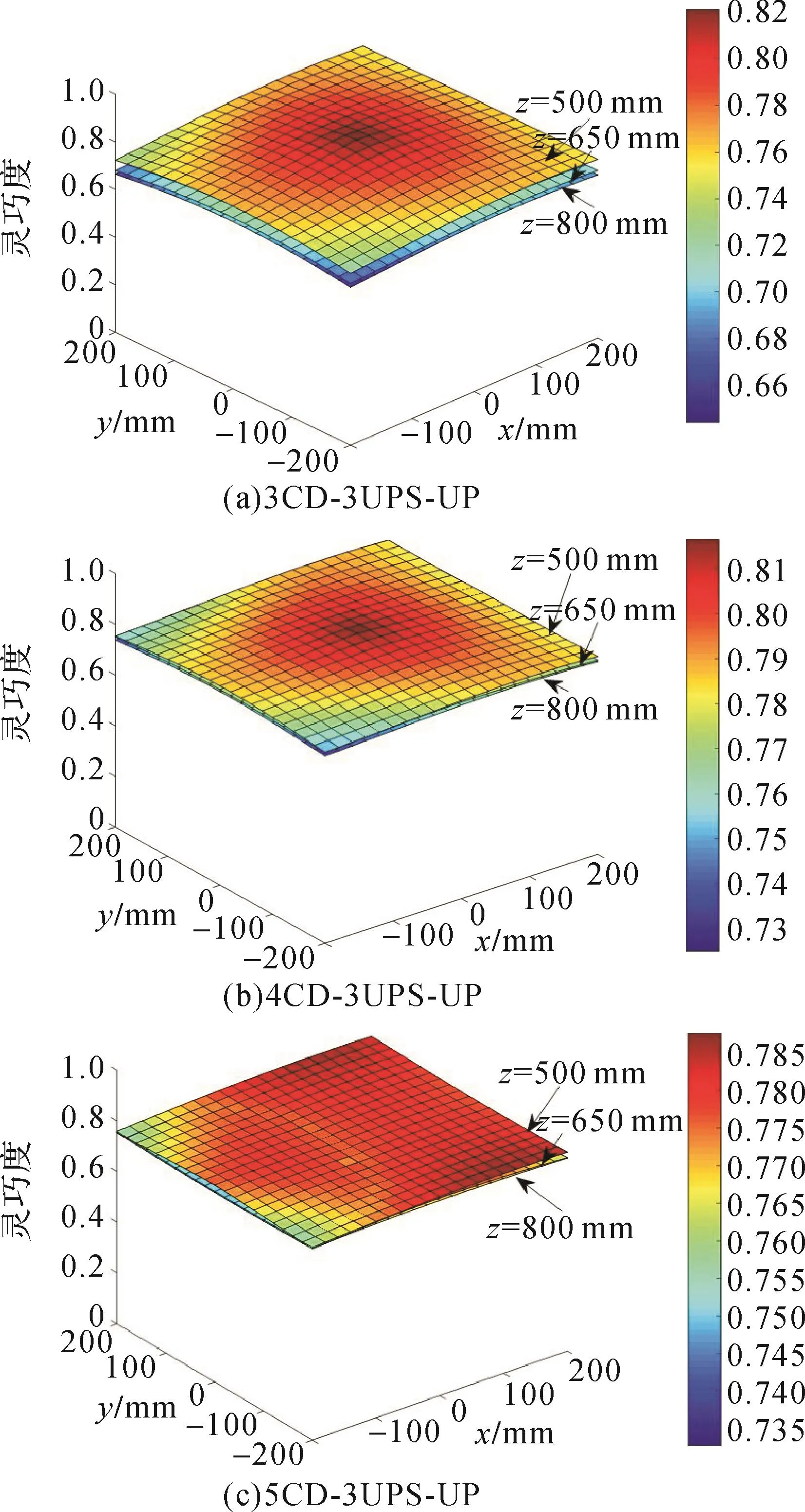
图5 不同刚柔协作混联机器人机构的灵巧度对比Fig.5 Comparison of dexterity of different rigid-flexible co-operative hybrid robot mechanisms

4.6 考虑灵巧性的工作空间

为实现刚柔协作混联机器人机构的灵活运动，需考虑灵巧性的约束，工作空间内灵巧度大于GCI的点的集合为刚柔协作混联机器人机构考虑灵巧性的工作空间。不同刚柔协作混联机器人机构考虑灵巧性的工作空间如图6所示。

由图6可知：不同刚柔协作混联机器人机构考虑灵巧性的工作空间不同；随着绳索数量的增加，刚柔协作混联机器人机构考虑灵巧性的工作空间不断减小，不利于抛光、打磨等工艺。

5 刚柔协作混联机器人机构绳索选择

综合考虑刚柔协作混联机器人机构的各项性能指标可知，绳索的数量和位置分布不同时，刚柔协作混联机器人机构的刚度、全域刚度、灵巧性、全域灵巧性以及考虑灵巧性的工作空间是不同的。因此当刚柔协作混联机器人机构用于抛光、打磨等工艺时，应根据实际工况选择合适数量的绳索进行布置：当主要工作高度为600 mm左右且对刚度和灵巧性的要求比较低时，使用3根绳索进行布置；当主要工作高度为530 mm左右且对刚度和灵巧性要求不是特别高时，使用4根绳索进行布置；当主要工作高度为490 mm左右且对刚度和灵巧性的要求较高时，使用5根绳索进行布置。