增材制造中基于零件特征的分段自适应分层算法
2020-07-21王春香郝志博
王春香,王 耀,郝志博
(内蒙古科技大学机械工程学院,内蒙古包头014010)
立体光刻(STL)模型的分层求交计算较为简单。国内外许多学者着重于STL模型的分层算法研究,其中自适应分层算法是目前的研究热点。例如:文献[1]提出了基于截面面积变化率的自适应切片算法;文献[2-3]提出利用相邻两层的面积偏差比控制分层厚度;文献[4]提出利用垂直分层轮廓曲线上点的切线角度决定分层厚度;文献[5-8]提出根据STL模型面片法向量、表面几何特征信息及弦高等因素进行分层厚度的自适应调整。上述自适应分层算法虽能提高分层精度和分层效率,但在对零件中能等厚分层且分层精度要求不高的非配对(配合)部分进行分层时,这些算法依然会不断地进行分层厚度的判定,导致分层时间增加,分层效率低下。
此外,在具有装配要求的零件的增材制造中,分段等厚分层算法具有一定的优势:可按精度要求进行分段。文献[9]提出了一种基于零件装配要求的分段等厚分层算法,即沿模型成型方向对零件进行分段,每段采用同一分层厚度,而各段的层厚不同。对在不同部位有不同精度要求的零件,分段等厚分层算法相较于等厚分层算法,能够根据不同的精度要求进行分段,使分层不受零件最低精度要求的限制,从而提高了分层效率。
综上所述,对于工程中应用广泛的具有复杂形状和配对(配合)要求且在不同部位有明显精度区别的零件的增材制造,现有的自适应分层算法和分段等厚分层算法虽各有优势,但其分层效率有待提高。若能结合自适应分层和分段分层的思路,则可进一步提高分层精度和分层效率,然而目前自适应分层算法无法与后提出的分段等厚分层算法融合使用。基于此,笔者融合上述2种分层算法的优势,提出了一种基于零件特征的分段自适应分层算法:根据零件的形状特征和不同的精度要求,沿成型方向对STL模型进行人工分段,并在分段的基础上利用最大尖端高度自适应调整每段分层的层厚。通过分段等厚分层算法和自适应分层算法的结合使用,使分层效果更优。
1 分段自适应分层算法的原理及实现
具有复杂形状和配对(配合)要求且在不同部位有不同精度要求的零件的增材制造,既需满足装配精度要求,又能在较短的时间内完成分层,且生产成本应相对较低。综合考虑装配精度、成型效率和成型成本,基于MATLAB软件,笔者提出一种分段自适应分层算法。当零件存在尖端部位时,利用该算法能保留其特征,降低特征畸形等问题的发生概率[10-14]。
1.1 零件STL模型的分段
根据零件的特性要求,沿着零件成型方向,利用等厚分层算法[15]将STL模型进行三次排序精简,使零件在分层方向上具有一定特征。在STL模型面片数据被有序整理后,按要求将模型划分为n段,将模型各段边界值按从小到大的顺序依次输入一个矩阵中,保证分层和模型成型按从底到顶的顺序进行。为保证程序整体的灵活性和各段的分层互不影响,在输入各段的初始分层厚度时,若各段的初始分层厚度相同,则只需输入一次,若各段的初始分层厚度不同,则须把各段的初始分层厚度按顺序输入另一个矩阵,保证与己分好的各段一一对应。
以各段边界值为界限,将属于该段的所有三角形面片数据从有序的STL模型中提取出来。经过排序处理后,沿着成型方向,先找到并排除三角形面片3个顶点的最大值小于较小边界值的所有三角形面片,接着将剩余三角形面片按其顶点坐标最小值进行排序,排除顶点坐标最小值大于较大边界值的三角形面片,剩余的三角形面片数据就是该段包含的所有数据信息。提取剩余的三角形面片(剩余矩阵),从边界值较小处开始对该段进行自适应分层处理。
1.2 模型各段的自适应分层
模型分段后,以法矢量自适应分层算法为基础,采用最大尖端高度限制法控制模型的成型精度。
各段自适应分层的实现过程为:将边界精度值、初始分层厚度和该段的数据输入自适应分层程序中,以边界值最小的边界为起点对该段分层,用该边界高度值作一次截交,得到该层轮廓线。以初始分层厚度(一般为最大分层厚度)对三角形面片法矢量最大值进行搜索,在排序整合过程中,程序自动将模型中的每个三角形面片的顶点坐标数据和法矢量数据储存在矩阵的行中,直接将索引指针指向法矢量在分层方向的最大分量的所在行,提取并将它作为该初始分层厚度下法矢量的最大值进行运算,利用法矢量与尖端高度之间的几何关系确定实际分层厚度。
控制阶梯效应以达到成型精度要求是自适应分层算法的关键。在STL模型中,阶梯效应主要受三角形面片与分层切片平面的位置关系的影响,其位置关系主要有2种:1)相邻2个分层切片平面与同一个三角形面片相交;2)相邻2个分层切片平面与多个(主要是2个)三角形面片相交。图1和图2分别为分层切片平面与不同数量三角形面片相交的示意图,其中:平面M是投影平面;S、S1、S2是三角形面片;o点是线段ab与分层切片平面Zi+1的交点a在分层切片平面Zi上的垂足。
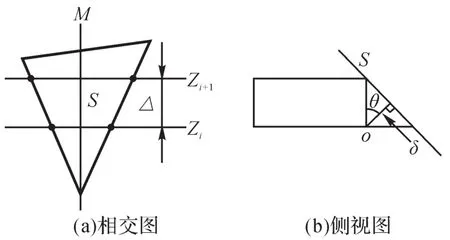
图1 分层切片平面与同一个三角形面片相交Fig.1 Intersection of layered slice planes and the same trian-gular plane
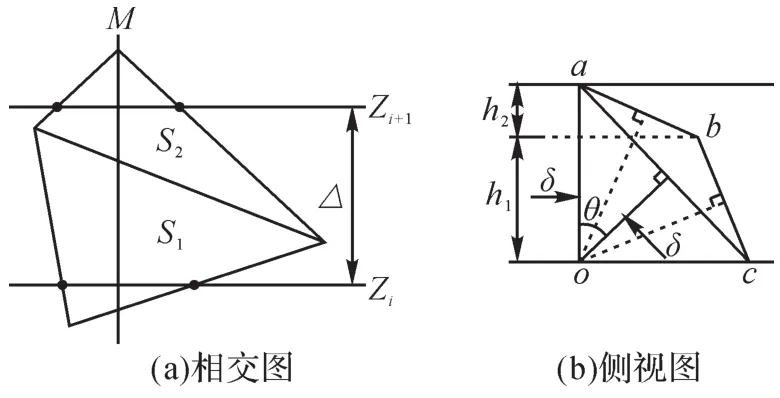
图2 分层切片平面与不同三角形面片相交Fig.2 Intersection of layered slice planes and different trian-gular plane
文献[16-18]介绍了分层切片平面与三角形面片的位置关系,并简略描述了其几何关系,但存在一定误差。其中,文献[16]以图2(b)中的δ作为其尖端高度,以其最大值作为分层厚度的判断依据。如果分层方向上2个相邻三角形面片之间的夹角小于90°,其模型误差会非常明显。如图2(b)所示,当切片平面与多个三角形面片相交时,影响模型误差的主要因素是o点到线段ac的距离与b点到线段ac的距离之和。过o点作线段ab、bc的垂线,垂线中总会存在长度大于δ且更加接近尖端高度值的线段。通过详细对比分层切片平面与三角形面片之间的位置关系,笔者提出一种基于最大尖端高度的限制法:将模型在该层内产生的所有尖端高度的最大值限定在精度范围内,即δmax≤δa(δmax为该层内所有三角形面片尖端高度的最大值,δa为所要求的精度),以控制模型各段的装配精度、形状等特性,将各段所要求的精度按矩阵形式对应上述边界值依次输入,即可保证模型的分段与分层精度对应,从而提高分层效率。
以零件STL模型中的每个三角形面片法矢量确定模型的自适应分层厚度。根据图2可得尖端高度δ与分层厚度△之间的关系:

式中:θ为三角形面片与水平面之间的夹角。
STL模型中存有每个三角形面片的法矢量,其种ni、nj、nk分别表示该法矢量在空间坐标系中x、y、z三个方向上的分量。依据该矢量信息可得到STL模型中每个三角形面片与水平面之间的夹角,而STL模型中每个三角形面片的法矢量都是一个单位向量,因此当分层方向为z向时,尖端高度δ与分层厚度△之间的关系也可以表示为:

当零件有装配要求时,其装配部位有过盈配合和间隙配合之分,本文通过三角形面片法矢量的方向来控制零件装配部位的过盈配合或间隙配合。当法矢量与成型方向的夹角为锐角时,成型时会产生成型余量;当法矢量与成型方向的夹角为钝角时,成型时会产生成型缺陷。成型误差是由阶梯效应及分层时上下轮廓线的选取所致,为满足零件的装配精度要求,根据夹角的大小自适应选择上下轮廓线。装配部位过盈配合:当夹角为锐角时,选择下轮廓线加工;当夹角为钝角时,选择上轮廓线加工。装配部位间隙配合:当夹角为锐角时,选择上轮廓线加工;当夹角为钝角时,选择下轮廓线加工。若装配部位没有过盈或间隙配合要求,则按照各分层轮廓线加工,无须选择上下轮廓线。
按照文献[15]提出的方法,对STL模型进行第2次排序时,用户给出初始分层层厚△初始和模型所要求的成型精度δa,找到法矢量在分层方向(z向)分量的绝对值最大的三角形面片,以该三角形面片法矢量的z向分量作为分层厚度的判断依据,即分层厚度△为:

由式(3)可知,由于选择的三角形面片法矢量的z向分量是最大的,则相应的实际分层厚度△就相对较小,阶梯效应也就较小,模型成型精度就易符合要求。
获得模型中某层的实际分层厚度后,利用分层平面的高度值,在排序完成的STL模型中直接提取仅与分层切片平面相交的三角形面片,然后进行求交运算。采用Trioutline函数进行求交运算,在无须建立拓扑关系的情况下,利用排序精简法直接提取与分层切片平面相交的所有三角形面片进行求交运算,快速输出封闭的轮廓线。分段自适应分层算法对轮廓线进行边求交、边输出,可减少内存占有量,提高分层效率。
各段之间的分层衔接是分段自适应分层的关键,衔接技术对成型精度与效率均有影响,当衔接出现问题时,会产生特征缺失等问题。因此,为避免出现该问题,在对零件某段进行自适应分层时,先搜索该段最大边界值,若初始分层厚度超出该段最大边界值时,则以该最大边界值与该分层厚度值的差值作为搜索范围,循环搜索直至确定最终分层厚度。这样段段累积,直到模型整体成型为止。
2 分段自适应分层算法的实例验证
对具有装配要求的斗齿类、链轨节类零件(各2个)的STL模型各进行10次分层测试,除了斗齿2的原型STL文件是由CAD(computer aided design,计算机辅助设计)实体模型转换外,其余3个均由实测点云转换获得。表1为基于分段自适应分层算法的各测试模型的分层时间,其中:t为10次测试的平均分层时间;tmin为10次测试次时间中的最小值。表2为在同一精度下基于分段等厚分层算法、自适应分层算法和分段自适应分层算法的各测试模型的分层时间。

表1 基于分段自适应分层算法的各测试模型的分层时间Table 1 Slicing time of each test model based on segmentation adaptive slicing algorithm
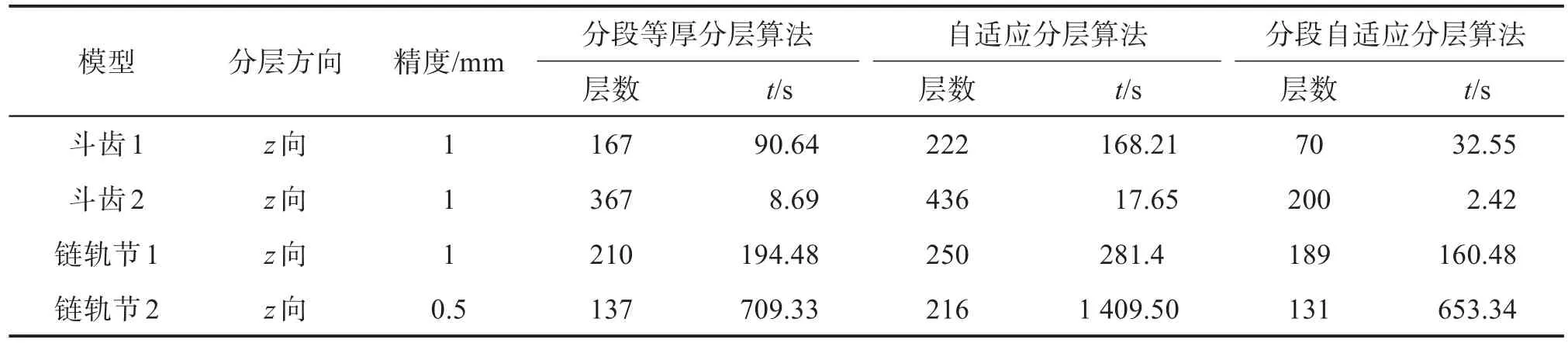
表2 在同一精度下基于不同分层算法的各测试模型的分层时间Table 2 Slicing time of each test model based on different slicing algorithms under the same accuracy
由于篇幅所限,仅列出斗齿1及链轨节1沿z向的分层效果图,初始分层厚度并非根据实际成型工艺所设,而是为了便于观察分层效果所设。
斗齿1的尺寸为97.64 mm×222.00 mm×89.69 mm,三角形面片数为101 462个,顶点数为50 727个。该零件具有内腔,且内腔两侧有同心的2个销孔,内腔和销孔均有装配要求,两者相较其他部位有明显的尺寸精度和形状位置要求。综合考虑该零件的装配精度要求及使用时铲尖极易磨损的情况,将其分为5段。斗齿1各段及整体的自适应分层结果如图3至图8所示。

图3 斗齿1顶部的自适应分层结果(精度为0.3 mm,层数为59)Fig.3 Adaptive slicing result at the top of dipper tooth 1(with precision of 0.3 mm,layer number of 59)
链轨节1的尺寸为132.16 mm×256.14 mm×111.4 mm,三角形面片数为150 715个,顶点数为753 48个。基于该零件定位孔和顶端圆柱孔的尺寸精度要求和形状位置要求,将它分成3段。链轨节1各段及整体的自适应分层结果如图9至图12所示。

图4 斗齿1中部的自适应分层结果(精度为0.6 mm,层数为49)Fig.4 Adaptive slicing result in the middle of dipper tooth 1(with precision of 0.6 mm,layer number of 49)

图5 斗齿1内腔顶部的自适应分层结果(精度为0.3 mm,层数为68)Fig.5 Adaptive slicing result at the top of inner cavity of dipper tooth 1(with precision of 0.3 mm,layer number of 68)
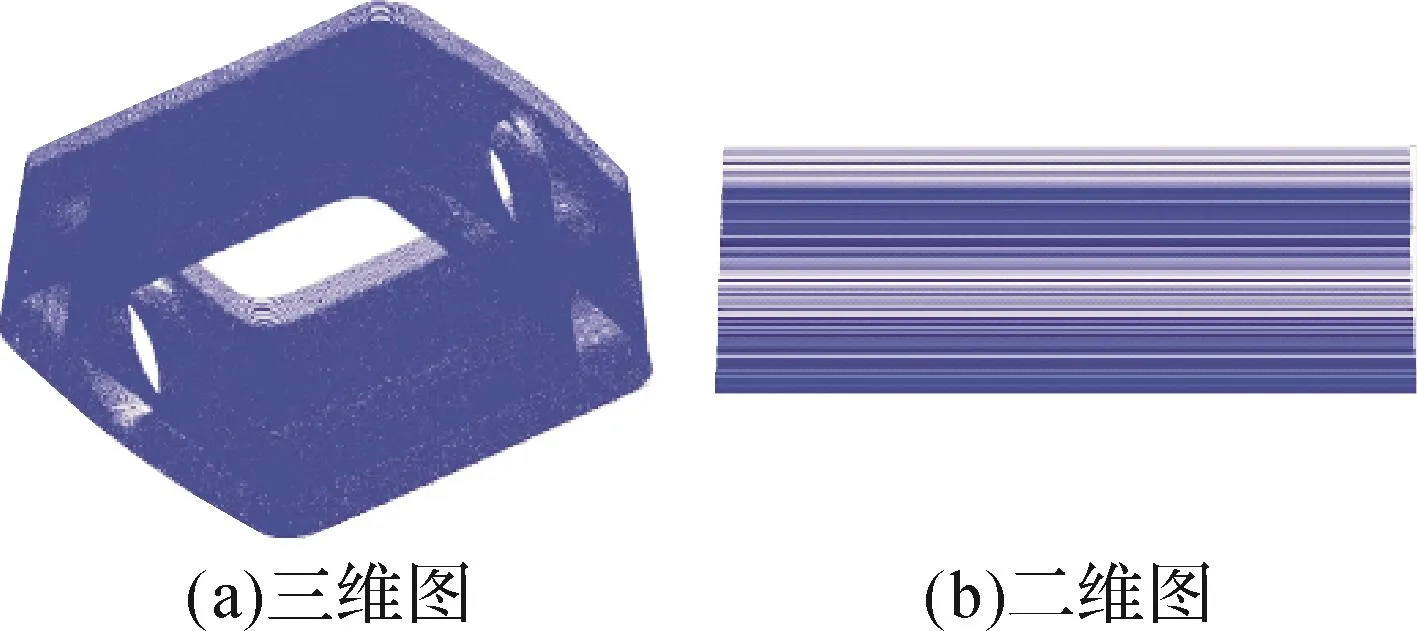
图6 斗齿1销孔的自适应分层结果(精度为0.1 mm,层数为221)Fig.6 Adaptive slicing result of pinhole of dipper tooth 1(with precision of 0.1 mm,layer number of 221)

图7 斗齿1底部的自适应分层结果(精度为0.3 mm,层数为25)Fig.7 Adaptive slicing result at the bottom of dipper tooth 1(with precision of 0.3 mm,layer number of 25)
观察各零件模型的分段自适应分层结果,可明显看出:按照精度要求的不同,模型被分为多段,各段内层厚分布是不均匀的,尤其是分层方向上形状变化较大的部位,其自适应分层的特征十分明显。在同一精度下,分段自适应分层算法的分层数明显减少,大幅度缩短了分层和成型的时间,提高了成型效率。

图8 斗齿1整体的分段自适应分层结果(层数为422)Fig.8 segmentation adaptive slicing result of integral model of dipper tooth 1(with layer number of 422)

图9 链轨节1底端圆柱孔的自适应分层结果(精度为1 mm,层数为76)Fig.9 Adaptive slicing result of cylindrical holes at the bottom of track link 1(with precision of 1 mm,layer number of 76)
图10 链轨节1定位孔的自适应分层结果(精度为1 mm,层数为181)Fig.10 Adaptive slicing result of positioning hole of track link 1(with precision of 1 mm,layer number of 181)

图11 链轨节1顶端圆柱孔的自适应分层结果(精度为1 mm,层数为62)Fig.11 Adaptive slicing result of cylindrical holes at the top of track link 1(with precision of 1 mm,layer number of 62)

图12 链轨节1整体的分段自适应分层结果(层数为319)Fig.12 Segmentation adaptive slicing result of integral mod-el of track link 1(with layer number of 319)
3 结论
分段自适应分层算法融合了分段和自适应分层原理,它与自适应分层算法的分层原理是完全相同的,不同之处在于前者可沿分层方向实现按需分割,使各段(零件的不同部位)按不同的表面误差或精度要求完成分层。分段自适应分层算法的特点如下:
1)在各段可实现较好的分层适应性,能保证复杂零件的形状特征和尺寸精度。
2)在满足精度要求的情况下,与分段等厚分层算法和自适应分层算法相比,其分层效率和成型效率明显提高(层数大幅减少),说明该算法能较好地协调精度与成型效率的关系。
3)分层稳定性及灵活性较好,且易于实现,便于操作。
4)更适用于结构的某一方向具有明显精度区别(如配合要求)、需要根据精度要求人工分段的复杂零件的增材制造。
5)可以解决尺寸大、超过设备成型范围而无法整体制造及需在成型方向的不同部位使用不同材料的零件的增材制造问题。
待研究的问题如下:根据人工经验选择分界线,进行模型分段,虽然简单、可靠,具有一定的实用性,但是对于不易于人工分段的零件,仍需进行智能分段的研究。目前国内外增材制造的设备均采用等厚分层,能实现自适应分层的设备只在极个别的实验室中试制。此外,对分段自适应分层算法的验证有待通过后期设计和搭建试验装置来实现。
