基于有限和瞬时旋量理论的Exechon并联机器人运动学分析

刘 卓，连宾宾,2，李 祺

（1.天津大学机械工程学院机构理论与装备设计教育部重点实验室，天津300354；2.天津大学仁爱学院机械工程系，天津301636；3.天津航天机电设备研究所，天津300301）

并联机器人具有刚度与体积比大、精度高、结构稳定及便于模块化设计等优点，广泛应用于航空航天装备、卫星跟踪系统的加工制造等现代尖端技术领域［1-4］。其中，具有一平动两转动（1T2R）运动形式的Exechon并联机器人可通过串接二自由度转头组成五自由度混联机器人，受到工业界和学术界的广泛关注［5］。

目前，Sun等［11］提出一种用于机器人设计的有限和瞬时旋量理论（FIS理论）：有限旋量可描述并联机器人的有限运动，即其位移；瞬时旋量用于表示并联机器人的速度。有限旋量和瞬时旋量之间的微分映射可以有效地反映位移和速度的关系，基于此，可在统一数学框架下建立并联机器人的拓扑模型和速度模型，为Exechon并联机器人的运动学分析提供新方法。

在机器人运动学分析中，首先在串联机器人运动学分析中引入雅克比矩阵的条件数，随后直接扩展到并联机器人，提出了局部条件数［12］、全局条件数［13］等一系列指标。然而，当采用这些指标来评价Ex-echon并联机器人的运动学性能时，结果存在严重的不一致性，无法用于指导机器人的分析和设计。

针对上述问题，笔者基于FIS理论，对Exechon并联机器人进行运动学分析，获得该机器人的拓扑模型和速度模型，并以无量纲的虚功率传递率作为性能指标来评价Exechon并联机器人的运动学性能，最后利用MATLAB软件分析Exechon并联机器人的局部虚功率传递率分布情况。

1 有限和瞬时旋量理论

根据Chasles有限位移定理，刚体的有限运动Sf可以表示为绕某一轴的转动与平移［14-17］：

式中：sf和rf分别表示运动轴线方向的单位向量和位置向量；θ和t分别表示刚体绕轴线的转动角度与平移距离。

当刚体实现2个连续的有限运动时，其运动可表示为：

式中：符号“△”表示旋量三角合成运算；Sf，q和Sf，h表示前后2个连续的有限运动。

基于Mozzi定理，刚体的任意瞬时运动可表示为绕轴线的转动角速度ω与平移速度v。则有限运动和瞬时运动之间的微分映射如下［18］：

式中：st和rt分别表示瞬时旋量轴线方向的单位向量和位置向量。

基于有限旋量和瞬时旋量及其微分映射关系，可以直接、简便地建立并联机构的拓扑模型和速度模型，为建立机器人运动学分析所用的雅克比矩阵提供了一种新的一体化方法。

2 Exechon并联机器人位置逆解

Exechon并联机器人由动平台、静平台、2条对称放置的UR支链和1条SR支链组成，其中3条支链均通过R副与动平台连接，UR支链和SR支链分别通过U副、S副与静平台连接，其虚拟样机模型和结构示意图如图1所示。图1（b）中：Ai点和Bi点（i=1，2，3）分别表示连接静平台的U副、S副中心和连接动平台的R副中心；△A1A2A3和△B1B2B3均为等腰直角三角形，其外接圆半径分别为a和b。以连线A1A3的中点为原点，建立静坐标系O-xyz，连线OA3为x轴，z轴垂直于平面A1A2A3向下，y轴满足右手定则；同理，以连线B1B3的中点为原点，建立动坐标系O′-x′y′z′，2个坐标系原点O和O′的距离为l。

图1 Exechon并联机器人虚拟样机模型和结构示意图Fig.1 Virtual prototype model and structure diagram of Ex-echon parallel robot

位置逆解求解是指在已知机构动平台位姿的情况下求得3条支链的杆长qi。当机构主动支链的长度发生变化后，动坐标系O′-x′y′z′相对于静坐标系O-xyz的旋转矩阵（绕x轴转动α，绕y轴转动β，绕z轴转动γ）可表示为：

式中：s和c分别表示sin和cos。

O′点在静坐标系O-xyz中的位置向量为：

根据图1（b），建立Exechon并联机器人的闭环矢量方程：

式中：si为第i条支链移动副的单位向量；rAi和rBi分别表示Ai点和Bi点的位置向量，且。

在式（6）两端点乘ci（ci为动平台上第i个R副轴线方向的单位矢量，ci=Rci0），可得：

由式（7）可得sγ=0，即γ=0°或者γ=180°，则旋转矩阵R可简化为：

综上，Exechon并联机器人的位置逆解可表示为：

3 基于旋量理论的速度模型

基于Exechon并联机器人的位置逆解，利用FIS理论构建该机器人的速度模型。其中，连接静平台的S副可分解为3个方向不同的R副，U副可视作由2个R副组成。因此，根据式（2），UPR支链和SPR支链的有限运动为：

式中：Sf，i表示第i条支链的有限运动；sx、sy和sz分别表示x、y和z轴方向的单位向量；θi，j和ti，j分别表示第i条支链第j个运动副的转动角度与平移距离。

Exechon并联机器人动平台的运动为支链运动的子集，满足多条支链求交运算，由式（9）可得Ex-echon并联机器人的拓扑模型：

根据式（3），对Exechon并联机器人的拓扑模型进行微分处理，可直接推导出该机器人的速度模型：

式中：Jl，E表示Exechon并联机器人速度雅克比矩阵；vz表示动平台沿sz方向的线速度；ωx和ωy分别表示动平台绕sx和sy方向的角速度；St，i，k表示第i条支链第k个关节的瞬时运动；t，i，k表示第i条支链第k个关节运动轴线方向的单位向量；，k表示第i条支链第k个关节的速度幅值，Ji表示第i个关节的所有单位旋量构成的矩阵。

根据速度旋量和力旋量之间的互易积关系，动平台约束力fc，i的雅克比矩阵可表示为：

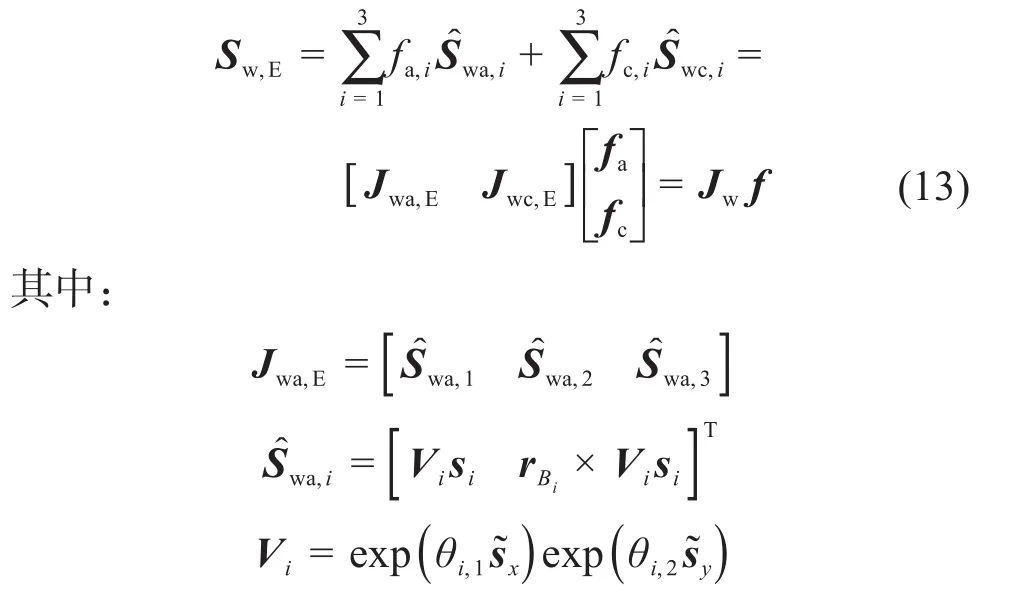
式中：fa，i为第i条支链受到的驱动力。

将Exechon并联机器人的驱动力旋量和速度旋量相乘，可得到其动平台与3个驱动关节之间的速度关系为：

4 Exechon并联机器人虚功率传递率分析

速度/力雅克比矩阵是反映机构输入输出速度/力的映射矩阵，对于同时具有平动与转动自由度的Exechon并联机器人而言，其速度雅克比矩阵包含线速度与角速度的映射关系，力雅克比矩阵包含力与力矩的映射关系。在以往的评价方法中，通常选取雅克比矩阵的数学特征如矩阵行列式、条件数、最大或最小奇异值以及灵巧度［19-20］等作为评价指标。采用这类指标评价Exechon并联机器人的运动学性能时，存在因线速度与角速度、力与力矩的量纲不一致而导致指标物理意义不明确的问题。针对此问题，定义虚功率传递率并将它作为性能评价指标，即通过求解力旋量与运动旋量的互易积，得到驱动力在对应的运动方向上所做的瞬时功或功率。

对于Exechon并联机器人，其第i条开环支链中运动副的自由度f＜6，Jw在规则的工作空间中满秩，则其速度模型可表示为：

式中：p是rp的斜矩阵；[TOJw]-T中的每一列表示Ex-echon并联机器人产生的许动或约束运动螺旋，则的每一行表示作用于动平台的对应驱动力或约束力螺旋；表示速度旋量沿轴线方向的单位向量；表示该速度旋量的大小。

对式（15）两边取wa，i的广义内积，可得：

式中：Sw，EQSt，E为Exechon并联机器人力螺旋与对应运动螺旋的瞬时功率，表征运动及力的传递效率。

由式（16）可知，不论St，E是移动旋量还是转动旋量，Sw，E是力旋量还是力偶旋量，Sw，EQSt，E的单位均为W，说明以瞬时功率评价Exechon并联机器人的运动学性能时量纲一致，它可表征支链运动及力的传递效率，物理意义明确。

基于上文建立的速度模型，Exechon并联机器人的虚功率传递率μi可表示为：

当μi趋近于0时，Exechon并联机器人的驱动力无法通过支链传递到动平台，则机器人将失去部分运动能力。为保证Exechon并联机器人具有良好的运动性能和驱动力传递性能，虚功率传递率应越大越好。因此，本文以各支链的最小虚功率传递率作为Exechon并联机器人的运动学性能评价指标，即：

式中：νE表示Exechon并联机器人的局部虚功率传递率。

由式（17）和式（18）可知，Exechon并联机器人的运动学性能随机器人位姿的变化而变化。结合Ex-echon并联机器人加工的工程需求，给出其尺寸参数和工作空间，如表1所示，其中：Dmax表示连杆之间允许的最大距离，θSmax和θUmax分别表示S副和U副的最大转角，lmin和lmax分别表示P副的最小移动值和最大移动值。

表1 Exechon并联机器人的尺寸参数和工作空间Table 1 Dimensional parameters and geometric condi-tions of Exechon parallel robot

在可达工作空间内，选择l=600，650，850 mm的3种位姿，利用MATLAB软件仿真可得到Exechon并联机器人的局部虚功率传递率的分布情况，如图2所示。

图2 Exechon并联机器人局部虚功率传递率的分布情况Fig.2 Distribution of local virtual power transmissibility of Exechon parallel robot

由图2可知：νE随l的增大而增大，且νE值均大于0，说明Exechon并联机器人各支链的速度和力均可有效传递至动平台，即该机器人在可达工作空间内具有较好的运动学性能，且不存在奇异位型；当θx=θy=0rad时，νE值较大，表明Exechon并联机器人的运动学性能较好；随着θx和θy的增大，νE值逐渐减小，即Exechon并联机器人的运动学性能随之变差。

综上可知，在一定的工作空间内，νE值可有效反映Exechon并联机器人运动学性能随位姿的变化情况，说明该指标可作为优化目标来指导Exechon并联机器人的优化设计。因此，结合工程经验和实际加工条件，可制造具有良好运动学性能的Exechon并联机器人物理样机。

5 结论

本文基于FIS理论对Exechon并联机器人进行了运动学分析，得到的结论如下：

1）在统一数学框架下实现了Exechon并联机器人拓扑模型与速度模型的构建，并根据FIS理论的微分关系简洁、直观地建立了Exechon并联机器人的速度/力雅克比矩阵。

2）针对Exechon并联机器人具有平动与转动自由度这一特点，定义了虚功率传递率并用它来表征机器人运动和力的传递效率，有效解决了平转耦合机构运动学评价指标量纲不统一的问题，为机器人机构后续的优化设计奠定了理论基础。