计及金属铰链的环形可展天线热-结构分析
2020-07-21武聪魁何柏岩袁鹏飞
武聪魁,何柏岩,袁鹏飞
(天津大学机构理论与装备设计教育部重点实验室,天津300350)
随着航天科技的发展,为满足航天器的电性能和使用要求,对其天线的形面精度和张力均匀性的要求越来越高[1]。环形可展天线的在轨服役环境十分恶劣,太空的极端环境条件会对天线的服役造成不同程度的影响,其中由空间辐射和空间低温引起的天线热变形是影响天线形面精度的重要因素[2-3]。环形可展天线主要由桁架、索网和铰链等组成,各结构所采用的材料不同,不同材料的结构对热变形的敏感性也不同[4],因此天线各结构的热变形程度存在差异。
国内外学者针对环形可展天线的热-结构分析展开了大量研究。例如:2010年,张惠峰等人[5]利用有限元方法分析了在轨运行环形可展天线在不同时刻的温度场和热变形,并采用热-结构耦合分析方法进行了算例分析,结果表明利用所用方法可实现天线从热分析到结构分析的直接转化和耦合;2012年,王斌[6]利用Pro/E软件建立了天线支撑机构——杆-铰链组件的几何模型,并在均匀温度场下进行了天线的热变形和热模态分析;2013年,Dicarlo等人[7]通过简化模型预测了昼夜温差对天线表面温度的影响;2016年,Guo等人[8]通过分析天线在轨热流的变化规律,计算了天线在热流影响下的温度场以及热变形情况,得到在热环境下天线电信号会失真的结论;2019年,贠海亮等人[9]利用有限元方法对环形可展天线进行热-结构分析,所得结果表明天线热变形使天线的形面精度严重恶化以及张力分布均匀性变差;2019年,Shen等人[10]研究了在空间环境中温度突变时环形可展天线的热致振动情况。然而,上述研究中对环形可展天线的空间热-结构分析均没有计及金属铰链部分,这主要是因为金属铰链结构复杂且其内部各部分之间存在间隙、接触和摩擦,在研究中难以建立如此复杂的实体模型,即使建立了金属铰链的实体模型,也会因模型过大而难以进行温度场的仿真分析。由于铰链的材料为铝合金,相对于桁架和索网所用的非金属材料而言,铰链具有更高的热吸收率和热膨胀率[11],且在天线结构中数量众多,因此它对天线热-结构分析的影响不容忽视。
基于此,笔者拟以环形可展天线为研究对象,考虑太空真实在轨服务环境中的各类因素,基于斯忒藩-玻尔兹曼(Stefan-Boltzmann)定律和傅里叶热传导理论,利用有限元软件UG建立计及金属铰链的环形可展天线的热辐射-热传导分析模型,求解其在轨非均匀温度场。同时,基于弹性热力学理论,利用有限元软件Abaqus建立计及金属铰链的环形可展天线的热变形分析模型,研究金属铰链在非均匀温度场下对环形可展天线形面精度及张力分布的影响规律,旨在为天线结构的设计提供参考。
1 环形可展天线结构及其性能评价指标
1.1 环形可展天线的结构
环形可展天线主要由前索网面、纵向索阵、周边桁架、后索网面和金属铰链五部分构成[12],如图1所示。其中:周边桁架作为环形可展天线的支撑结构,由多个平行四边形桁架单元通过金属铰链连接而成;前、后索网面由柔性索连结而成,与纵向索阵相互作用形成类似抛物面的索网面;金属铰链分为同步铰链和T形铰链,用于连接周边桁架。
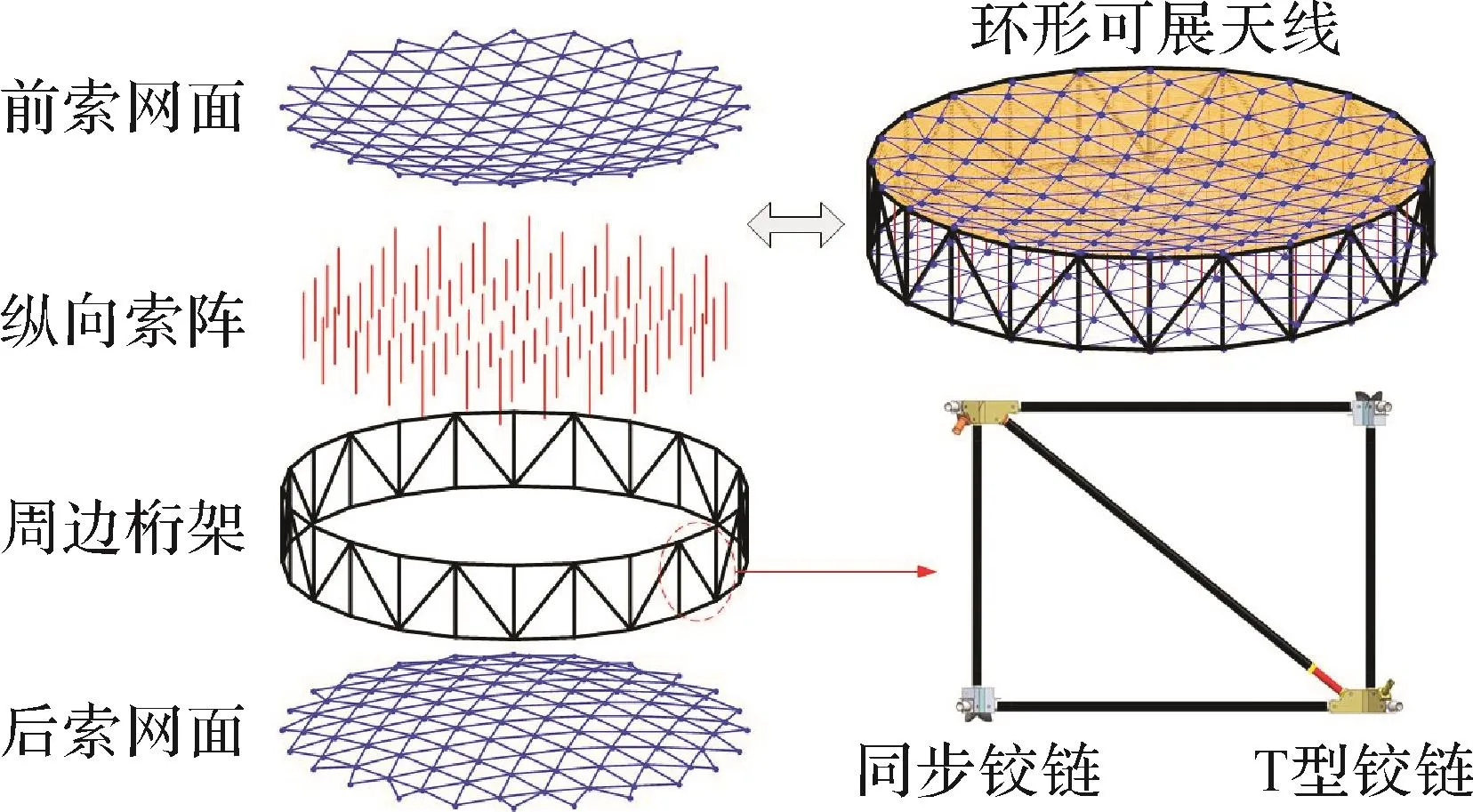
图1 环形可展天线的结构示意图Fig.1 Structure diagram of hoop deployable antenna
1.2 环形可展天线的性能评价指标
环形可展天线的性能评价指标主要包括天线的形面精度和张力比。
1)形面精度。
在设计阶段,环形可展天线的形面误差主要包括原理误差及设计误差,通常以设计误差来描述天线的形面精度[13]。通过求解实际前索网面和理想前索网面之间所有对应节点坐标差的均方根R来获取天线的设计误差。如图2所示,设理想前索网面上的任一节点为Mi(xi,yi,zi),实际前索网面上与其对应的节点为M′(x'i,y'i,z'i),在全局坐标系下x、y、z方向上两节点的坐标差分别为ΔXi、ΔYi和ΔZi,则:

式中:k为前索网面的节点总数。

图2 天线的设计误差示意图Fig.2 Schematic diagram of design error of antenna
2)张力比。
环形可展天线为一种张拉整体结构,其内部张力的分布形式并不唯一。考虑到天线的结构力学性能,其内部张力分布应尽可能均匀,即索网的张力比越小越好[14]。索网的张力比η为:

式中:Fmax为索段的最大张力;Fmin为索段的最小张力。
2 环形可展天线的热-结构分析模型
2.1 环形可展天线的热辐射-热传导分析模型
环形可展天线在轨运行时会时刻受到空间热源的强热辐射,且其内部结构之间存在热传导,因此需建立天线的热辐射-热传导模型,以分析其温度分布。在时空域中,温度T是关于空间位置(x,y,z)和时间t的函数,可表示为T(x,y,z,t)。根据傅里叶热传导理论,在笛卡尔坐标系下,三维非稳态导热微分方程的一般形式为:

式中:ρ为微元体密度;c为微元体的比热容;Φ为单位时间、单位体积中热源的生成热;μx、μy、μz分别为微元体在x、y、z方向的导热系数。
设实际物体对所有波长的发射率均为常数,基于Stefan-Boltzman定律,物体的辐射力M(T)可表示为:

式中:ε为物体的发射率;φ为Stefan-Boltzman常数。
环形可展天线热辐射-热传导的微分方程可表示为:
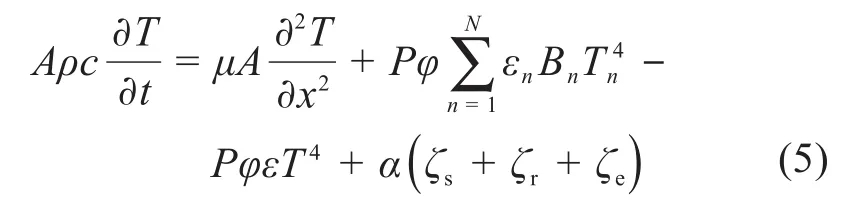
式中:A为天线单元的截面积;μ为天线材料的导热系数;P为单元的截面周长;εn为第n个单元的表面发射率;Bn为第n个单元的热辐射吸收率;α为单元所接受到空间外热流的面积因子;ζs、ζr、ζe分别为单元单位面积上的太阳辐射能、地球反照能和地球辐射能;Tn为第n个单元的温度。
由此可知,影响环形可展天线在轨温度场的主要因素是天线各部分结构材料的导热系数、表面发射率和吸收率等。因此,在计算环形可展天线的空间温度场时,须将天线模型与真实天线各结构的热辐射和热传导进行近似等效。
2.2 环形可展天线的热变形分析模型
利用热辐射-热传导分析模型得到环形可展天线的在轨温度场后,对环形可展天线结构进行热变形分析。由弹性热力学理论可知,当环形可展天线各结构间存在温差ΔT(x,y,z,t)时,相应的热膨胀量为αTΔT(x,y,z,t),其中αT为材料的热膨胀系数。根据广义胡克定律可得环形可展天线的热变形方程为[15]:
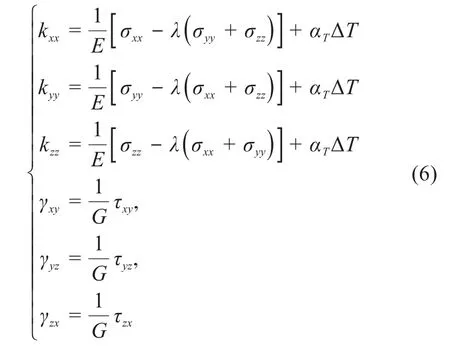
式中:kxx、kyy、kzz为应变分量;σxx、σyy、σzz为应力分量;E为材料的弹性模量;G为材料的剪切模量;λ为材料的泊松比;γxy、γyz、γzx为剪切应变分量;τxy、τyz、τzx为剪切应力分量。
由此可知,对环形可展天线热变形影响最大的因素为温差、材料热膨胀系数及弹性模量等。因此,在计算环形可展天线的热变形时,须将天线模型与真实天线各结构的变形进行近似等效。
基于上述热力学理论分析,利用有限元软件建立计及金属铰链的环形可展天线的热-结构分析模型。
3 计及金属铰链的环形可展天线的建模方法及算例
3.1 计及金属铰链的环形可展天线的建模方法
环形可展天线的结构包括前后索网面、纵向索阵、周边桁架和金属铰链,通过有限元软件Abaqus对环形可展天线建模。桁架和索段结构简单,易于建模,其中:前后索网面和纵向索阵的材料为Kevlar,采用T3D2柔性索单元进行建模;桁架由横杆、竖杆和斜杆组成,其材料为碳纤维,采用B33梁单元建模。首先,基于上述方法建立不计及铰链的环形可展天线的模型。为使环形可展天线的索网形成一定的网面形状,须对模型进行找形处理[16]。
环形可展天线中的金属铰链数量较多,其结构复杂且内部各部分之间存在间隙、接触和摩擦,难以精确建模,因此须对铰链结构进行简化。将结构复杂的金属铰链简化为具有一定长度和截面尺寸(与实际尺寸相等)的梁单元。金属铰链分为同步铰链和T型铰链,将同步铰链简化为4个节点和3个杆单元,将T型铰链简化为6个节点和5个杆单元,各杆单元之间通过Bushing单元进行连接[17]。杆单元采用B33梁单元,杆的类型为空心杆,长度为a,外径为b,壁厚为h,如图3所示。
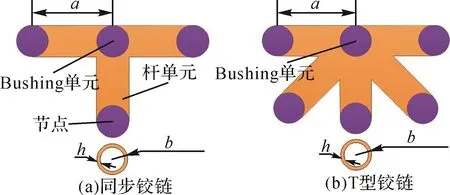
图3 金属铰链的简化模型Fig.3 Simplified model of metal hinge
在不计及铰链的环形可展天线模型的基础上,建立计及金属铰链的环形可展天线模型,通过在节点处引入Bushing单元[17]计及金属铰链的刚度。在计算环形可展天线的温度场时,将简化铰链的材料属性按真实铰链的材料属性进行设置,以满足热辐射和热传导的近似等效。在计算热变形时,将简化铰链视作桁架杆单元的一部分,忽略简化铰链的热变形,这是因为简化铰链的结构不完全等同于真实铰链,简化铰链没有真实铰链的力学特性,导致铰链的实际热变形无法准确获得。
3.2 计及金属铰链的环形可展天线建模算例
以口径为16 m、焦距为10 m、高度为3.4 m的三十单元环形可展天线为例,利用上述方法对它进行建模。在计及金属铰链的环形可展天线的模型中,索段共有481根,前、后索网的节点数各为61个;桁架杆件共有120根,桁架节点数为60个;金属铰链共有60个,同步铰链和T型铰链各为30个,铰链的节点总数为300个,杆单元设为空心杆,空心杆的长度为7×10-2m,外径为2.5×10-2m,壁厚为3×10-4m。环形可展天线各部分结构的材料属性如表1所示。

表1 环形可展天线各部分结构的材料属性Table 1 Material properties of each structure of hoop deployable antenna
在建立计及金属铰链的环形可展天线模型时通过引入Bushing单元来计及铰链的刚度,故须对金属铰链进行刚度测量实验[17]。具体实验方法为:固定金属铰链后,通过液压机施加压力和扭矩,并利用位移传感器测得相应位移,以测得金属铰链在如图4所示的局部坐标系下x,y,z方向的拉伸刚度和旋转刚度。金属铰链刚度的实验结果如表2所示。
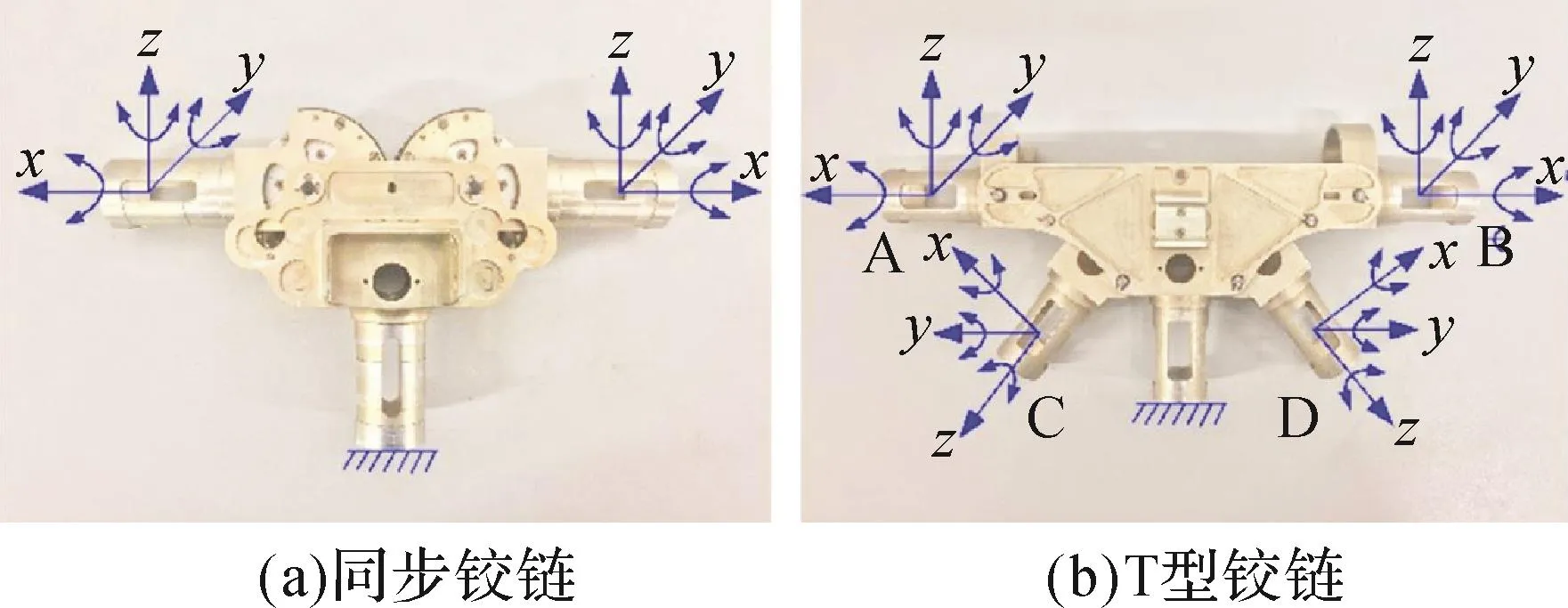
图4 金属铰链的刚度测量方向Fig.4 Measuring direction of stiffness of metal hinge

表2 金属铰链刚度的实验结果Table 2 Experimental results of stiffness of metal hinge
基于环形可展天线各部分结构的材料属性和金属铰链的刚度,建立找形后的计及金属铰链的环形可展天线的有限元模型,如图5所示。
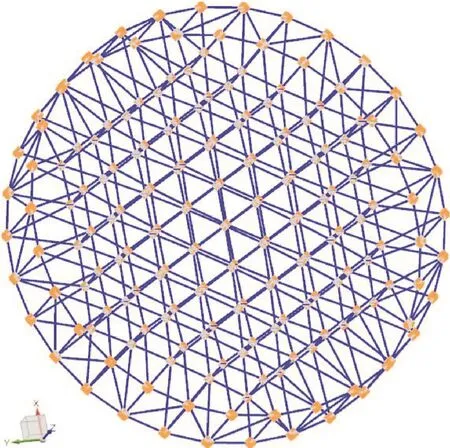
图5 计及金属铰链的环形可展天线的有限元模型Fig.5 Finite element model of hoop deployable antenna with metal hinges
4 环形可展天线的温度场与热变形计算
4.1 环形可展天线温度场的影响因素及基本假设
基于环形可展天线的真实在轨服役环境,考虑空间真空、空间低温、微重力和空间热源等因素对环形可展天线温度场的影响。影响因素的设定及基本假设为:
1)空间真空。只考虑天线与外部环境的热辐射和天线自身结构间的热辐射和热传导。
2)空间低温。把空间环境看作绝对黑体,其空间温度为-269℃。
3)微重力。忽略天线自身重力对变形的影响。
4)空间热源。当天线进入地球轨道后,空间热源主要为太阳辐射热。
根据不同时节的太阳辐射强度,取春分日、夏至日、秋分日、冬至日的太阳辐射通量分别为1 377.8,1 323.6,1 357.4,1 411.6 W/m2。通常将地球看作温度为-23℃的绝对黑体,其一年的平均反照率为0.3[18]。
4.2 环形可展天线在轨运行位置的划分
以对地静止轨道作为环形可展天线的运行轨道,轨道高度为35 786 km,轨道倾角为0°,偏心率为0,运行周期为86 400 s[19]。在春分日和秋分日,太阳直射赤道,在运行轨道上形成时长为4 170 s的阴影区;在冬至日和夏至日,太阳直射南、北回归线,不会形成轨道阴影区。将环形可展天线的在轨运行位置划分为24个,取其中4个为特征位置,分别定义为侧照位置6、正照位置12、侧照位置18以及背照位置24,如图6所示。
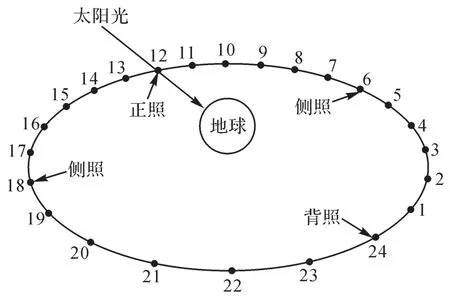
图6 环形可展天线在轨运行位置示意图Fig.6 Diagram of position of hoop deployable antenna in orbit
4.3 环形可展天线温度场的计算
利用有限元软件分别计算在春分日、夏至日、秋分日和冬至日计及与不计及金属铰链的环形可展天线的在轨温度场。设初始温度为0℃,图7至图10所示分别为在以上4个计算日环形可展天线处于特征位置时的温度云图。

图7 在春分日环形可展天线处于背照位置24时的温度云图Fig.7 Temperature cloud map of hoop deployable antenna at back-illuminated position 24 on the spring equinox day
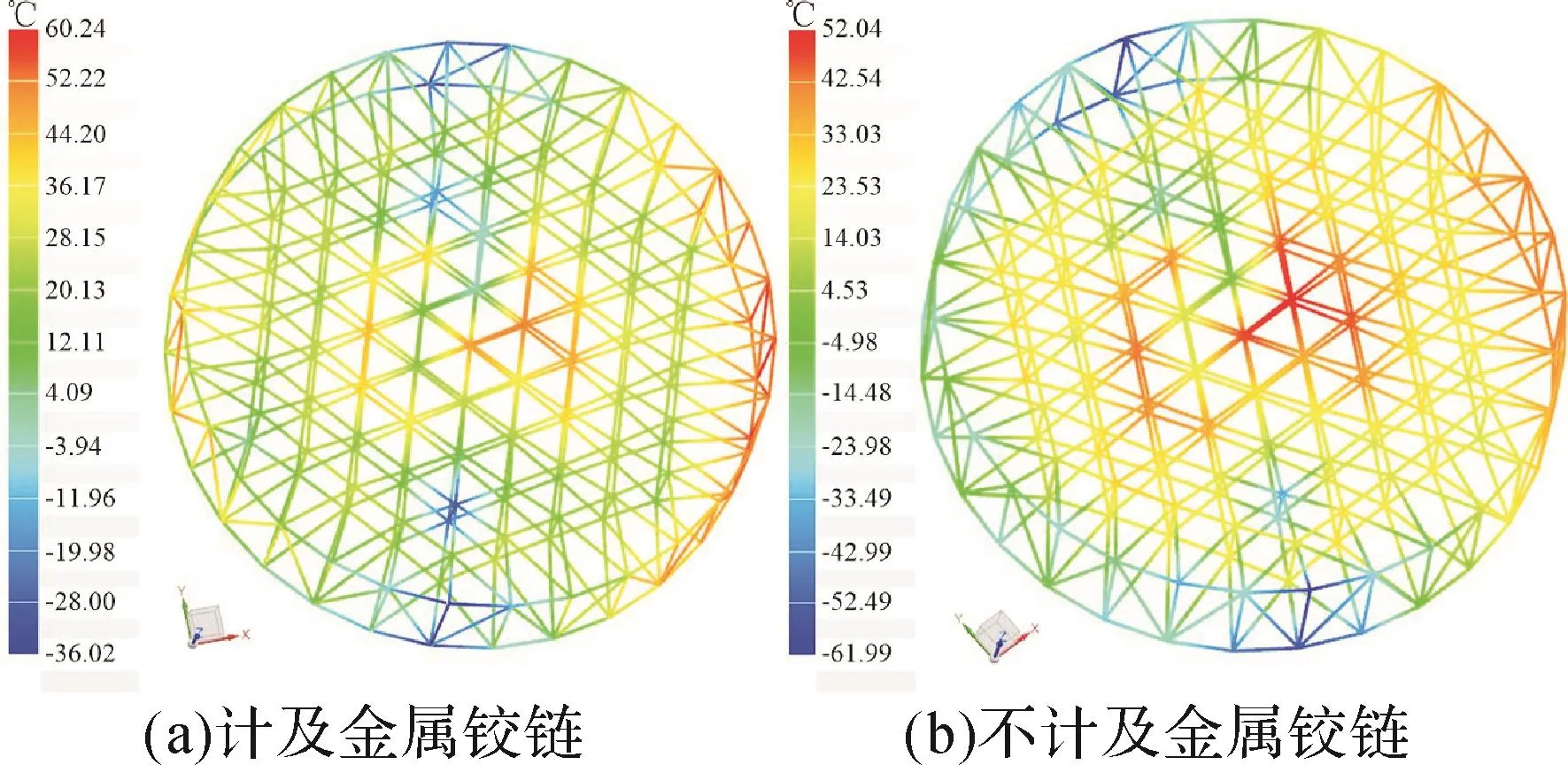
图8 在夏至日环形可展天线处于侧照位置6时的温度云图Fig.8 Temperature cloud map of hoop deployable antenna at side-illuminated position 6 on the summer solstice day

图9 在秋分日环形可展天线处于正照位置12时的温度云图Fig.9 Temperature cloud map of hoop deployable antenna at front-illuminated position 12 on the autumnal equinox day
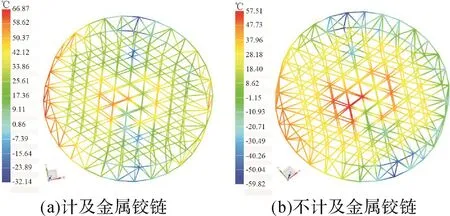
图10 在冬至日环形可展天线处于侧照位置18时的温度云图Fig.10 Temperature cloud map of hoop deployable antenna at side-illuminated position 18 on winter solstice day
通过比较环形可展天线模型各节点的温度差可知,环形可展天线在春分日处于背照位置24时的温度差最大,故下文仅展示天线在该天、该位置时桁架和前后索网各个节点的温度曲线,如图11至图13所示。
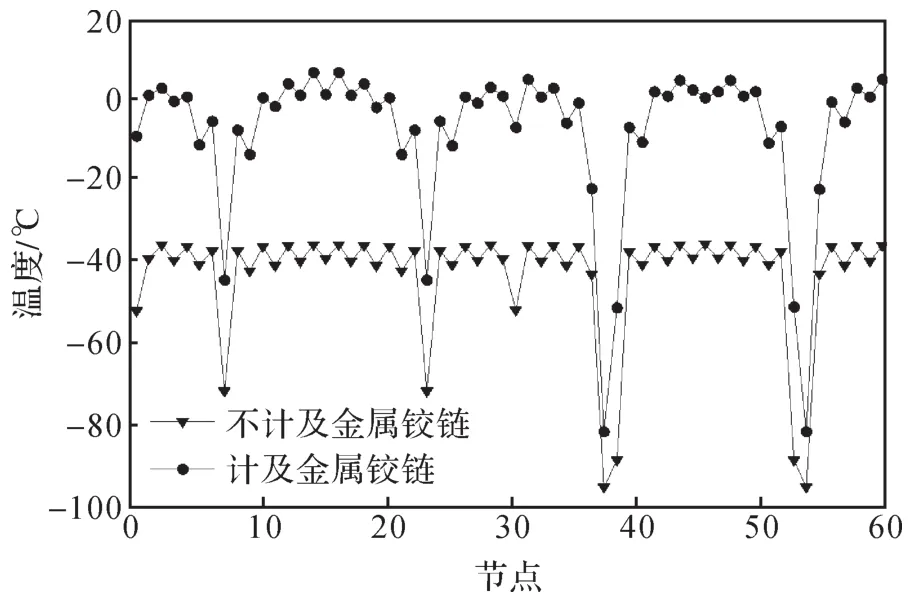
图11 桁架节点温度比较Fig.11 Comparison of temperature of truss nodes

图12 前索网面节点温度比较Fig.12 Comparison of temperature of front cable mesh sur-face nodes
通过比较可知:
1)计及与不计及金属铰链的环形可展天线在春分日的温度分布规律近似相同,但是金属铰链对天线的最低温度和最高温度均有巨大影响。
2)金属铰链对桁架节点温度的影响很大。在春分日背照位置24时,计及金属铰链的环形可展天线桁架节点的温度比不计及金属铰链的最多高45.10℃。

图13 后索网面节点温度比较Fig.13 Comparison of temperature of rear cable mesh sur-face nodes
3)金属铰链对索网节点温度的影响相对较小。在春分日背照位置24时,计及金属铰链的环形可展天线索网节点的温度比不计及金属铰链的最多高17.56℃。
4.4 环形可展天线热变形的计算
基于计算得到的温度场,对环形可展天线施加温度载荷,计算其热变形,并求得天线热变形后的形面精度和张力分布情况。图14所示为在春分日环形可展天线处于所有24个位置时的形面精度变化曲线,图15至图17所示为天线各结构的张力比曲线。
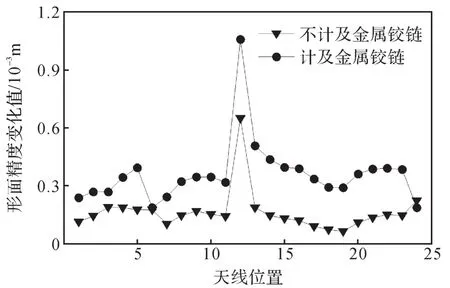
图14 在春分日环形可展天线的形面精度变化曲线Fig.14 Variation curves of surface accuracy of hoop deploy-able antenna on the spring equinox day
由形面精度变化曲线可知:
1)相较于不计及金属铰链的环形可展天线,计及金属铰链的环形可展天线处于各个位置时的形面精度都产生了不同程度的恶化,其在14个位置处的形面精度变化值超过了3×10-4m,最大超过了1×10-3m,而不计及金属铰链的环形可展天线仅在正照位置12时的形面精度变化值超过3×10-4m。
2)计及金属铰链的环形可展天线的形面精度的变化值波动更大,处于背照位置24时形面精度的变化值仅为1.9×10-4m,但处于正照位置12时形面精度的变化值为1.05×10-3m,已达到毫米级;而不计及金属铰链的环形可展天线的形面精度的变化值最大为6.5×10-4m,最小为6×10-5m。
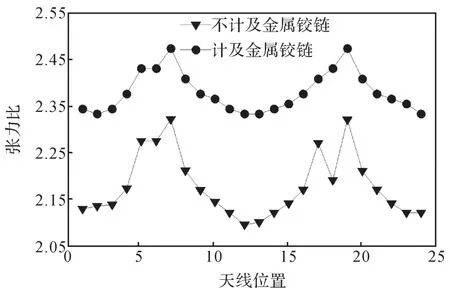
图15 在春分日环形可展天线前索网面的张力比曲线Fig.15 Tension ratio curves of front cable mesh surface of hoop deployable antenna on the spring equinox day

图16 在春分日环形可展天线纵向索阵的张力比曲线Fig.16 Tension ratio curves of longitudinal cable of hoop de-ployable antenna on the spring equinox day

图17 在春分日环形可展天线后索网面的张力比曲线Fig.17 Tension ratio curves of rear cable mesh surface of hoop deployable antenna on the spring equinox day
3)处于正照位置12时环形可展天线形面精度的变化值达到峰值,这是因为此时太阳光直射天线的后索网面,前索网面被遮挡,由此产生了很大的温度差,从而导致处于该位置时天线形面精度的变化值达到峰值。
由张力比曲线可知:
1)处于位置6和位置18时,计及与不计及金属铰链的环形可展天线的张力比均产生波动,这是因为处于这2个位置时,天线的一侧被太阳光直射,另一侧被遮挡,导致两侧存在较大温差,从而造成张力分布不均。计及金属铰链的环形可展天线的张力比恶化明显,张力比最大达2.47。
2)计及与不计及金属铰链的环形可展天线的前后索网面和纵向索阵的张力分布的规律近似相同,计及金属铰链的环形可展天线处于各个位置时的张力比均比不计及金属铰链的大。
5 结 论
1)计及与不计及金属铰链的环形可展天线模型在同一时刻的温度场相差很大,尤其是在铰链和桁架节点处。在空间热环境中,金属铰链对环形可展天线温度场的影响很大。
2)通过环形可展天线的热变形分析可知,金属铰链的热效应严重影响天线的形面精度,形面精度的变化值已经达到毫米级;同时天线各结构的张力比也会产生不同程度的恶化,影响天线在轨服役的稳定性。
3)研究结果可为同类型环形可展天线的热-结构分析提供借鉴,对天线结构设计有指导意义。设计时应注意金属铰链及其他结构的热防护,比如喷涂热防护涂层或采用热不敏感材料等来降低其对天线结构的影响,以保证天线在服役时的结构稳定性以及信号传输的鲁棒性和可靠性。
