插值型无单元伽辽金比例边界法理论及研究进展分析

叶文华，王 娟

(新余学院 建筑工程学院，江西 新余 338004)

0 引言

近年来，无网格法发展迅速，相比成熟的有限元法，该方法在数值计算时不需要生成网格，而且特别擅长处理不连续及大变形问题。最近发展起来的无单元伽辽金比例边界法巧妙地继承了比例边界有限元法与无网格法的长处。然而，这种看似完美的数值方法以移动最小二乘法为基础得到的试函数却不满足Kronecker delta函数性质，致使本质边界条件施加困难。经过许多专家学者对该近似方法的研究改进，最终王聚丰等[1]介绍了一种改进的插值型移动最小二乘法，这种方法有效克服了移动最小二乘法的不足，而且可以任意选用非奇异权函数。目前，有学者根据该插值方法提出了插值型无单元伽辽金比例边界法(Interpolating Element-Free Galerkin Scaled Boundary Method，简称IEFG-SBM)。研究表明，采用IEFG-SBM分析一些工程实际问题具有较高的精度与效率。

1 插值型无单元伽辽金比例边界法的理论基础

1.1 改进的插值型移动最小二乘法

假定在一段光滑边界Si上布置N个点s1,s2,…,sN，取p1(s),p2(s),…pm(s)为给定用来形成逼近函数的基函数，其中p1(s)=1。将给定的基函数转化为一组新的基函数，令

(1)

(2)

对函数u(s)也作与式(1)相同的转化，即

(3)

(4)

式中：

(5)

u=(u(s1),u(s2),…u(sn))T

(6)

(7)

(8)

式中：wI(s)可取作任何非奇异的权函数，eI为1×n的单位行向量且第I列元素为1。

(9)

v(s)=(v(s,s1),v(s,s2),…,v(s,sn))

(10)

根据式(3)和式(4)，可以得到u(s)的逼近函数为

(11)

其中形函数矩阵为

Φ(s)=(φ1(s),φ2(s),…,φn(s))

=v(s)+gT(s)A-1(s)H(s)

(12)

gT(s)=(g2(s),g3(s),…,gm(s))

(13)

(14)

1.2 控制方程

(15)

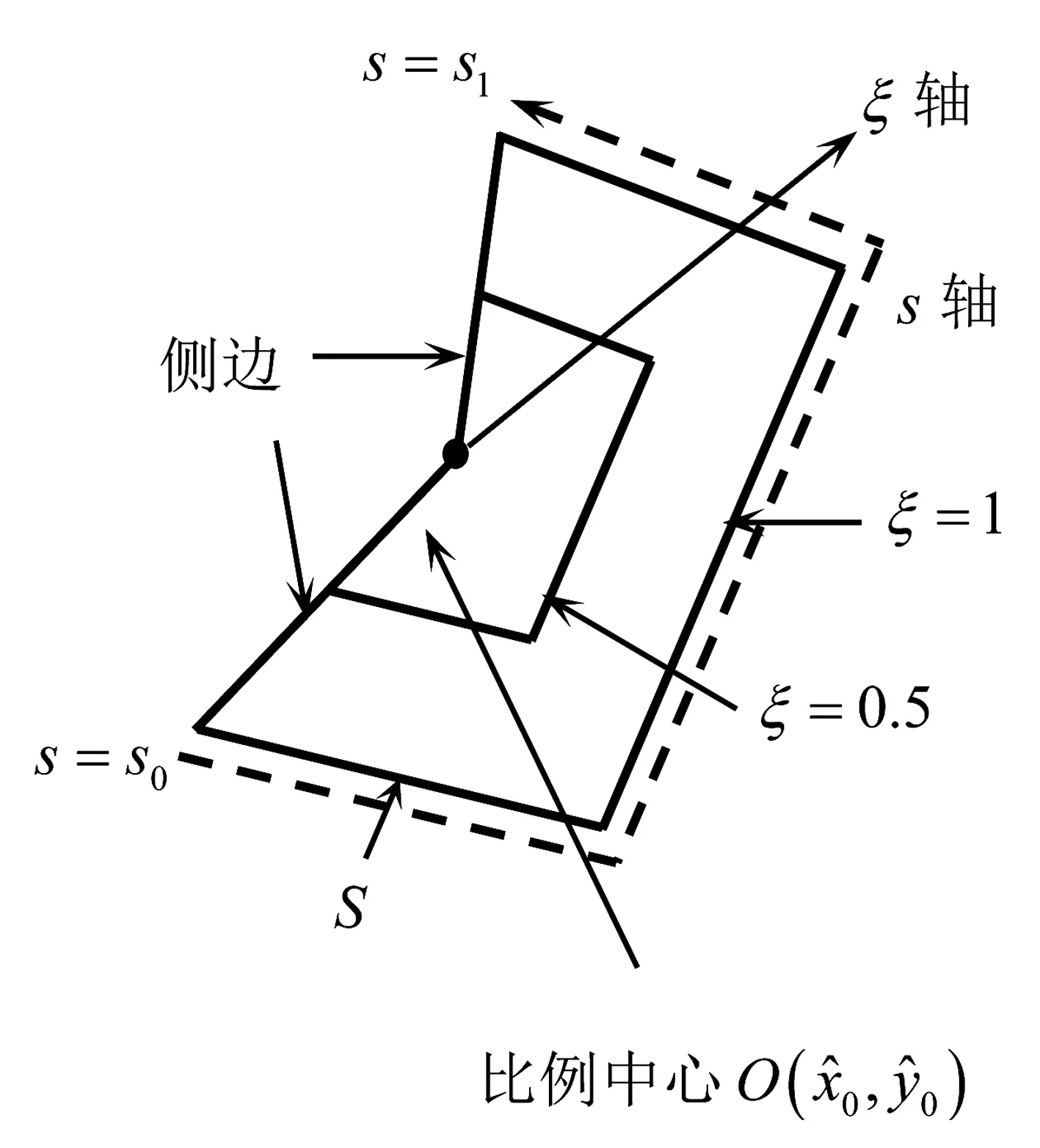
图1 比例边界坐标系Fig.1 Coordinate system of proportion boundary

基于式(11)，计算域内任意点处的位移u(ξ,s)可以近似表示为

(16)

式中：Φ(s)为形函数，u(ξ)为径向上的节点位移函数。

将式(16)代入虚功原理，可推导出IEFG-SBM的控制方程为

(17)

(18)

式中：P为等效节点力向量，E0，E1和E2为系数矩阵。

2 插值型无单元伽辽金比例边界法的研究进展

相对于传统的无单元伽辽金法，IEFG-SBM在计算精度与效率方面具有明显优势。陈莘莘等[2-3]首次提出IEFG-SBM并利用该方法准确分析了弹性与压电材料断裂问题。同时，为了更好发挥IEFG-SBM和有限元法各自的优势，提出了将IEFG-SBM与有限元法进行耦合并用于解决弹性与压电材料断裂问题[4-5]。

3 展望

随着研究的不断深入，IEFG-SBM在断裂以及无限域问题处理中已显示出其良好的快捷性与适应性。尽管近年来该方法的应用范围在不断扩大，但至今应用该方法求解的都是线性问题，非线性还未涉及，未来将扩大IEFG-SBM的应用范围，进而为计算方法的发展带来更为广阔的前景。

第11卷 第14期2020年7月黑龙江科学HEILONGJIANG SCIENCEVol.11Jul.2020