第一换元法求不定积分的技巧

武文娟

(广州工商学院 基础教学部，广州510850)

求不定积分的方法很多，主要有直接积分法、第一换元法、第二换元法、分部积分法。第一换元法(又称凑微分法)是求不定积分最常用的方法，灵活性大、技巧性强，是最难掌握的一种方法。虽然看似形式多样，但并不是毫无技巧可言。本研究将依据被积函数的特点提出第一换元法求不定积分的解题技巧。

1 第一换元法的定义

设f(u)具有原函数F(u)，u=φ(x)可导，则有以下第一换元公式：

=F(u)+C=F(φ(x))+C

2 第一换元法的应用

3 第一换元法求不定积分的难点

4 第一换元法求不定积分的技巧

第一换元法求不定积分的关键是找到合适的中间变量u=φ(x)。以下将给出第一换元法求不定积分的技巧，共分三步：第一，把被积函数看成几个因式的乘积，找出其中最复杂的因式。第二，与基本积分表对照，找出与复杂因式最相似的公式。第三，根据最相似的基本积分公式找出中间变量。运用以上三步技巧可以快速有效地帮助学生找到中间变量u=φ(x)，可以灵活应用第一换元法求解定积分。

5 典型例题

以下将通过典型例题具体阐释第一换元法求不定积分的技巧。这个技巧对于求不定积分是行之有效的，能帮助学生从容运用第一换元法求定积分。

例：计算下列不定积分

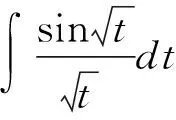
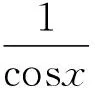
解：令u=cosx，则du=-sinxdx，于是

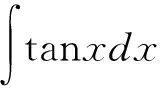
=-ln|u|+C=-ln|cosx|+C

解：令u=2-3x，则du=-3dx，于是

解：令u=xlnx，则du=(1+lnx)dx，于是

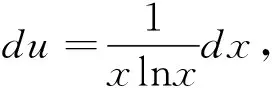
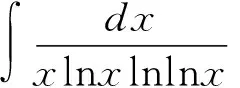
=ln|u|+C=ln|lnlnx|+C