形状优化的装配式软钢阻尼墙抗震性能及其对钢框架结构变形的控制

陈 岩 ，李 妍

(1. 长春建筑学院 土木工程学院，吉林 长春 130607；2. 吉林建筑大学 土木工程学院，吉林 长春 130118)

地震往往会造成巨大经济损失与人员伤亡，减小地震对建筑结构的损伤并在震后可快速恢复功能日益引起世界地震工程界的广泛关注[1,2]。而近年来，随着我国城市建设水平的不断提高，高层钢结构被越来越多地应用于经济核心区的工业建筑、商业建筑以及城市地标性建筑，该类建筑人口密集且功能相对复杂，一旦地震中断功能，将影响整个城市的运转，为减小结构在地震中的损伤，提高震后可快速恢复能力，一个行之有效的方法是将地震产生的能量引导到不易损伤且易于修复的构件上去，利用该类构件强大的塑性变形能力以及往复滞回性能来耗散地震能量，保护主体结构不受损伤，震后通过更换该类构件实现主体结构的功能恢复，这种构件亦称为阻尼墙。

1972年Kelly等[3]提出的剪切钢板阻尼墙(Steel Panel Wall，SPW)，被广泛应用于高层结构的消能减震中，矩形耗能墙片通过焊接与其他部分连在一起，而研究表明，焊接区域存在两种不利应力，一是由弯矩与剪切力共同引起的等效应力过于集中，二是焊接热应力对阻尼墙的承载力削弱十分明显[4]。国内外学者通过引入加劲肋、局部削弱耗能墙片厚度以及运用多种材料合成等手段来改善上述问题[5～7]。但并未从根本上改善连接区域的等效应力集中以及热应力显著的问题。

本文针对上述两个问题，设计了一种无焊接装配式构造的形状优化软钢阻尼墙(Steel Optimized Panel Wall，SOPW)，如图1所示。通过5种高宽比的SPW与SOPW进行拟静力对比数值仿真分析，检验本文优化方法的效果，并将其应用于某典型结构的1榀3跨9层钢框架结构中进行动力分析，检验本文提出的阻尼墙减震能力。

图1 阻尼墙的构造

1 阻尼墙的构造与设计公式推导

1.1 阻尼墙的构造

为了解决传统钢板阻尼墙连接区域的焊接热应力问题，本文利用螺栓连接设计了可更换型阻尼墙。其构造形式如图1所示，包括耗能墙片、L形连接构件，由于耗能墙片的高厚比较大，易出现面外屈曲，为此设计了两侧的防屈曲措施并与支座连为一体，L形连接构件与上下框架梁之间可以通过承压型螺栓连接，也可以将这部分提前与梁焊接在一起。耗能墙片的有效高度为h，宽度为b，厚度为t。为了提高阻尼墙的耗能能力，本文将传统矩形阻尼墙的形状进行如下规则优化：如图1中的耗能墙片所示，以1.5倍墙片宽度为半径，沿墙片中位线向左右两侧设定圆心画圆，与墙片的上下边缘相交组成优化型的耗能墙片形状，下面对其力学性能以及耗能能力进行讨论。

1.2 阻尼墙的设计公式推导

首先推导矩形阻尼墙的承载力公式，若给定阻尼墙受到的剪切力为V，取V1，V2为V的两个代表值，则由剪切力V1引起的阻尼墙边缘弯矩M为：

M=V1h/2

(1)

那么由弯矩M引起的横截面正应力最大值为：

(2)

式中：墙体截面的惯性矩I=tb3/12，t为耗能墙片的厚度。

由剪切力V2引起的截面剪应力为：

(3)

式中：系数取值1.5是由于剪应力沿横截面呈抛物线分布，因此取为峰值。

因此，当给定阻尼墙的尺寸以及材料强度时，其端部的剪切力V，即抗剪承载力可按照下式计算：

V=min[V1，V2]

(4)

优化型阻尼墙的承载力Vo可按下式计算：

Vo=αV

(5)

式中：α为强度修正系数，其取值将在下文中进一步讨论。

2 阻尼墙数值仿真

2.1 材性试验

为了充分发挥阻尼墙的耗能能力，本文采用低屈服点LYP160钢材的本构模型进行数值仿真分析。根据GB/T 228.1—2010《金属材料拉伸试验方法》对耗能墙片进行4个标准材性试验，如图2所示，采用50 mm量程引申计测位移，荷载通过材性试验机读取，除去1个断裂位置在引申计测量位置之外的试验件，其余3个试验结果列于表1，平均屈服强度195 MPa，平均极限强度301.4 MPa，极限应变的平均值为69.4%，强屈比平均为1.55，可见低屈服点钢材表现出良好的延性，适用于制作耗能构件。

图2 材性试验构件及测试装置

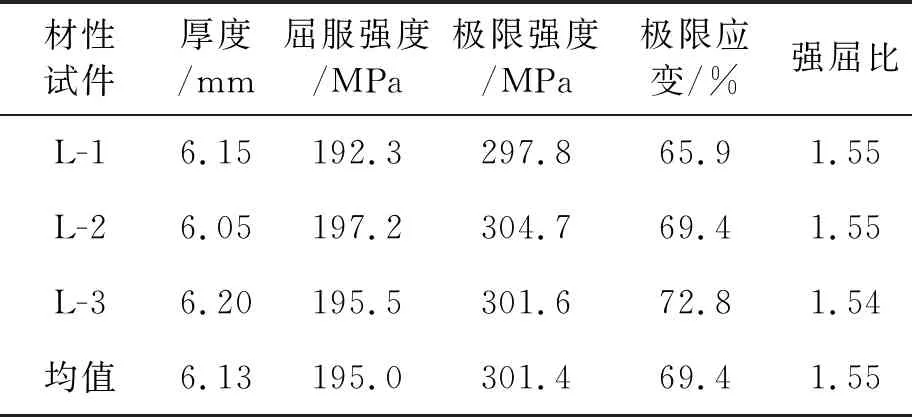
表1 材性试验结果

2.2 参数设计

为了比较阻尼墙优化前后的力学性能，参考文献[8～10] 中尺寸，设计5组厚度t为6 mm，高宽比λ(λ=h/b)分别为0.9，1.0，1.1，1.2，1.3的软钢阻尼墙进行拟静力仿真模拟，每组均设有一个等高等宽的矩形阻尼墙进行对比，参数如表2所示。采用有限元软件ABAQUS进行仿真分析，选择3D-shell单元模拟耗能墙片，材料强化模型采用非线性随动硬化模型，屈服点取195 MPa，塑性本构关键参数如表3所示。如图3所示，首先定义上下2个刚性连接，将边缘约束等效为节点约束，根据实际边界条件，将墙片下端固定，上端约束转动，并施加水平往复荷载，加载制度如图4所示，约束所有节点的面外位移。

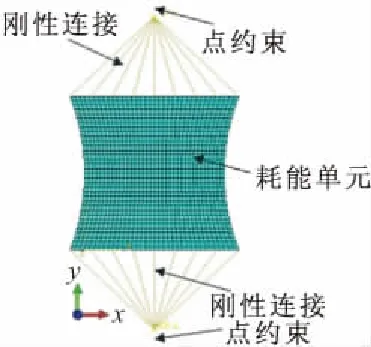
图3 阻尼墙仿真模型

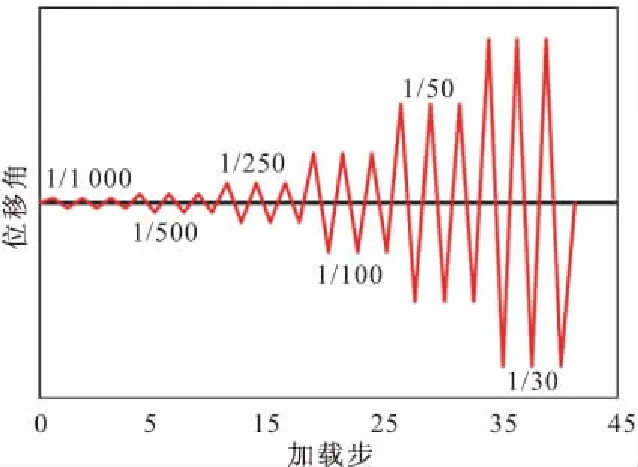
图4 拟静力加载制度

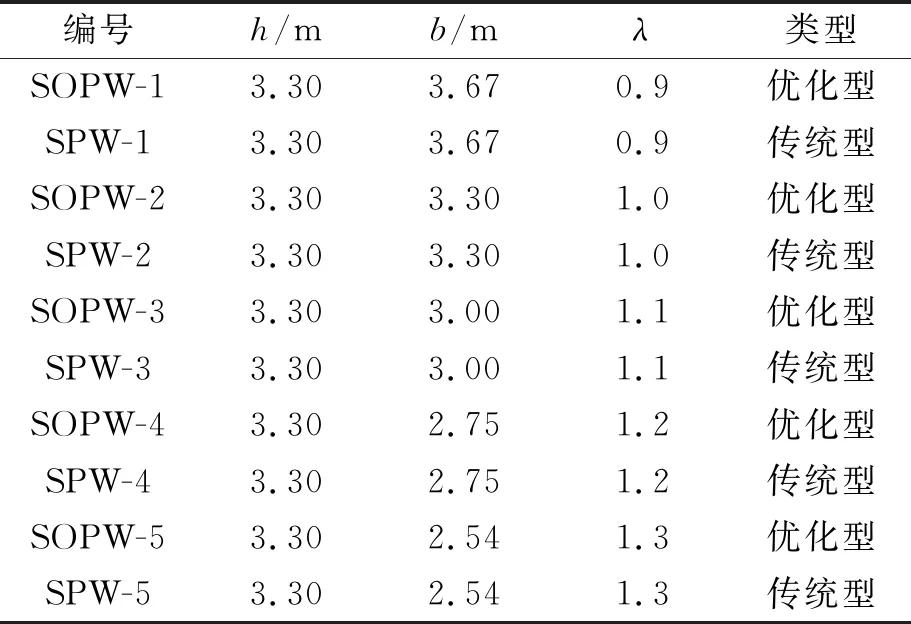
表2 模型参数

表3 仿真模型本构关键参数

2.3 数值仿真结果分析

图5所示为数值仿真得到的1组典型的阻尼墙优化前后滞回曲线，优化后的阻尼墙承载力增加，滞回环面积增大，说明其耗能能力更强；而且，相比优化前的阻尼墙而言，优化型阻尼墙的承载力变化较为稳定，从进入屈服至加载结束，滞回曲线上的每一个工况下的峰值力几乎保持在一条水平线上，说明优化型阻尼墙的力学性能稳定，可以稳定地耗散地震能量。将5组阻尼墙的优化耗能超越比η(优化前阻尼墙耗能与优化后阻尼墙的比值)列于表4，由表可知，在1/1000剪切角时，阻尼墙优化耗能超越比为0，此时各模型保持弹性；在1/500剪切角时，优化后的阻尼墙耗能超越比均超过100%，最大至135.2%，说明优化型阻尼墙在相同位移工况下，耗能能力明显提高。将5组阻尼墙的累积塑性应变列于表5，该物理量为金属变形能力的重要指标，可直观反映金属低周疲劳性能。由表5可知，优化后的阻尼墙累积塑性应变均减小了80%以上，说明阻尼墙的形状经过优化以后，在相同位移工况下，金属的疲劳效应明显减轻；图6为阻尼墙优化前后累积塑性应变分布云图，可以看出，传统形状的阻尼墙四个角部区域的应力非常集中，而优化后的阻尼墙塑性分布更加均匀，应力集中现象得到了明显改善，这样的受力模式极大地提高了阻尼墙的耗能能力与力学稳定性能。

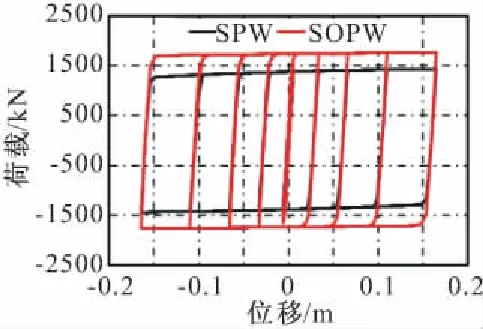
图5 典型的(λ=1.1)阻尼墙优化前后滞回曲线

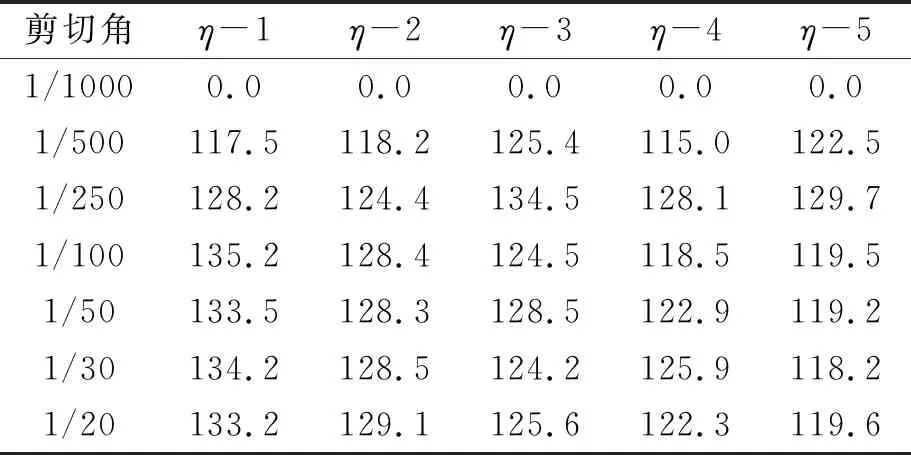
表4 阻尼墙优化耗能超越比η %

表5 阻尼墙优化前后累积塑性应变ε

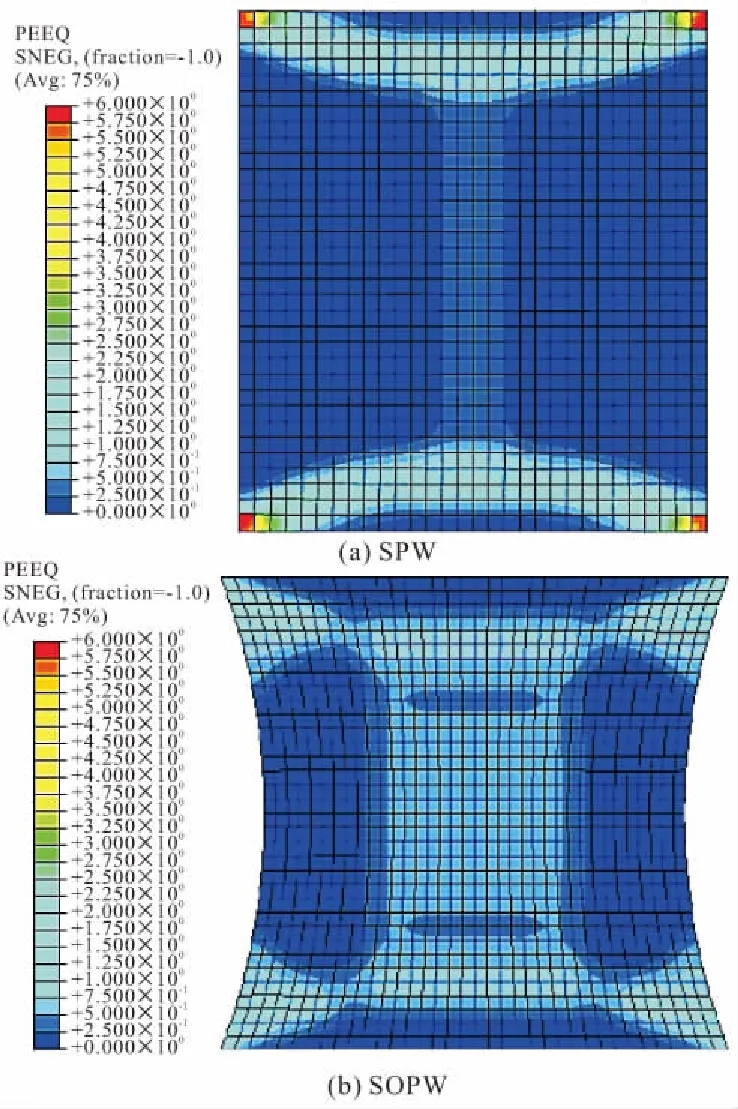
图6 阻尼墙优化前后累积塑性应变云图

将抗剪承载力的公式计算结果与有限元结果进行比较，结果列于表6。由表6可知，SPW的设计公式计算结果与有限元结果误差在2%左右，验证了计算公式的准确性。由SOPW与SPW的有限元计算结果可以看出，相同λ的SOPW承载力约为1.25倍的SPW，因此建议公式中强度修正系数α取1.25。

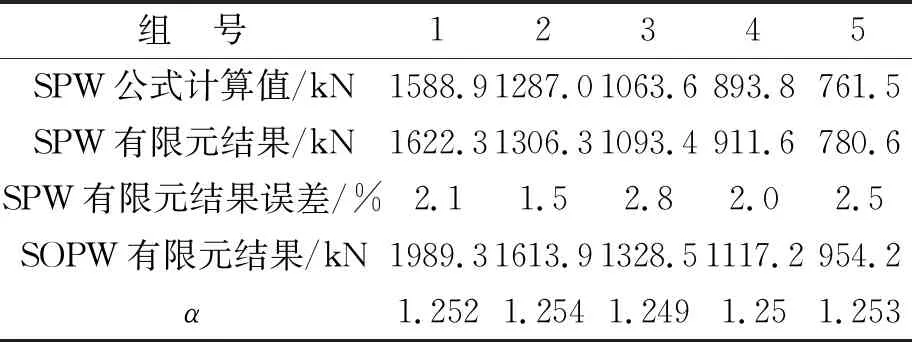
表6 阻尼墙抗剪承载力

3 钢框架地震响应控制分析

为了控制钢结构的损伤，提高钢结构地震可恢复性能，根据结构与构件的尺寸，将第3组SOPW应用于某典型1榀3跨的9层钢框架结构[11]，该结构层高3.3 m，柱距4.5 m，8度设防，Ⅱ类场地，各层均布恒载8.0 kN/m2，均布活载2.0 kN/m2。为了提高运算效率并且说明问题，本文仅研究该结构的平面力学行为，各层荷载平均分配到梁柱节点。结构构件材料采用Q235级钢，数值本构采用随动硬化模型，屈服点为235 MPa，弹性模量为2.06×105MPa，泊松比为0.3。而SOPW阻尼墙仍采用低屈服点钢LYP160，本构关系按照上文材性试验的真实数据输入。结构的梁、柱截面分别为H200×200×8×12和H250×250×9×14，在有限元软件中分别采用梁、柱单元进行建模，梁柱之间固定连接，阻尼墙与梁之间固定连接，结构与地基固定连接，约束结构的面外位移，有限元模型如图7所示。原始结构用OR(Original)表示，消能结构用EC(Energy Consumption)表示，带有矩形(Rectangle)阻尼墙的消能结构为EC-R，带有优化型(Optimized)阻尼墙的耗能结构为EC-O。

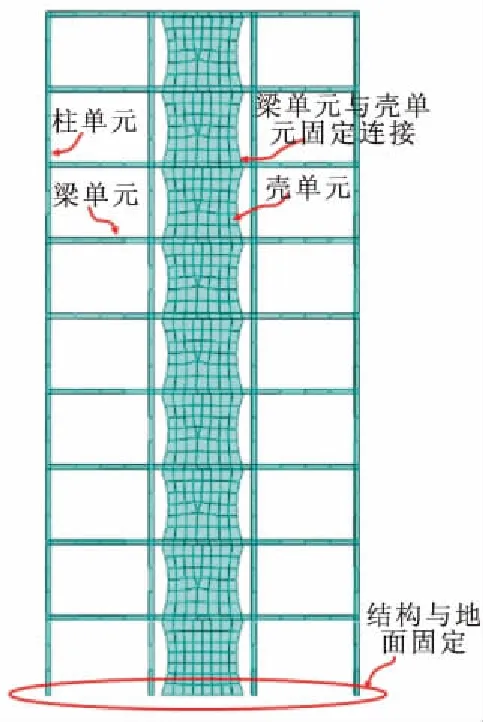
图7 钢框架结构有限元模型

本文按照地震反应谱接近设计谱的原则，对该结构底部输入El-Centro地震动、卧龙地震动、Taft地震动，地震反应谱如图8所示，时程如图9所示。加速度峰值PGA分别为0.2g(中震)与0.4g(大震)，提取结构在中震与大震下的地震响应。图10所示为消能结构与传统结构的最大层间位移角对比曲线。

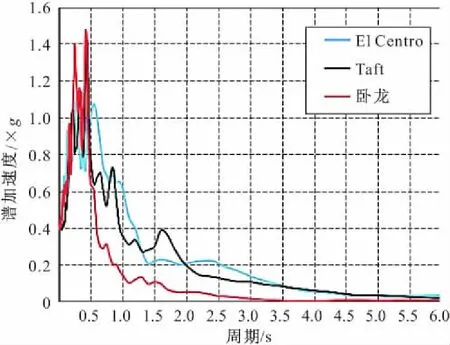
图8 3条地震动反应谱

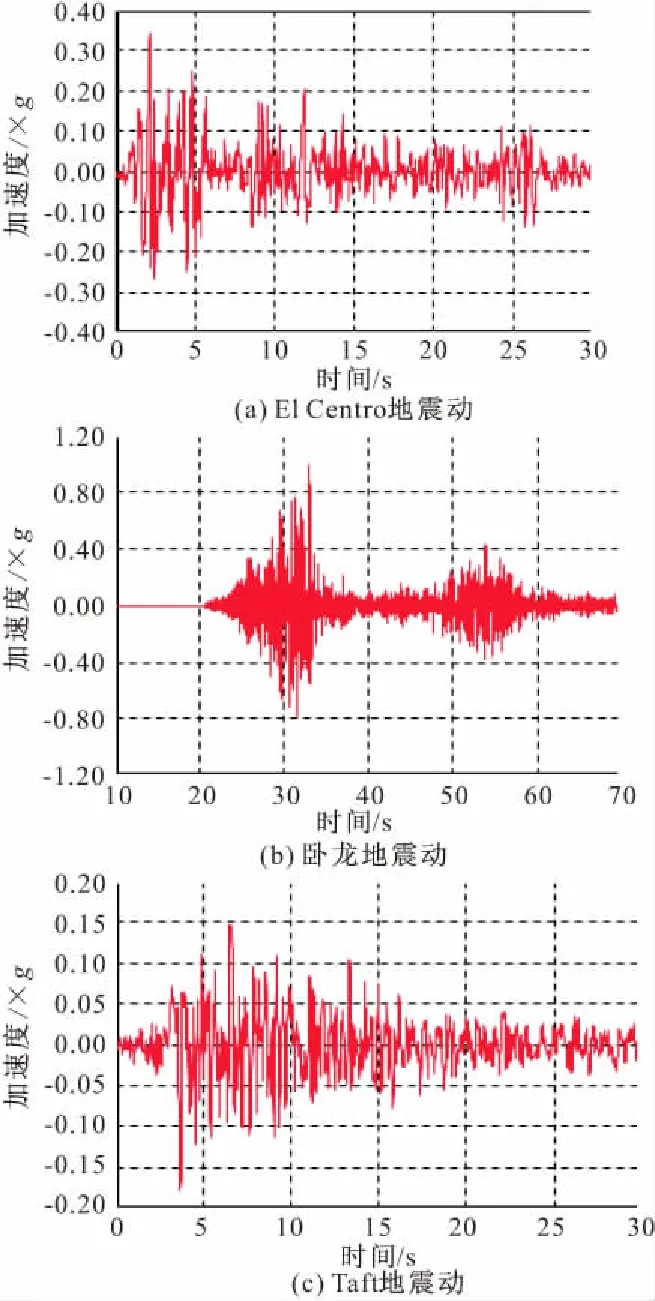
图9 3条地震动加速度时程

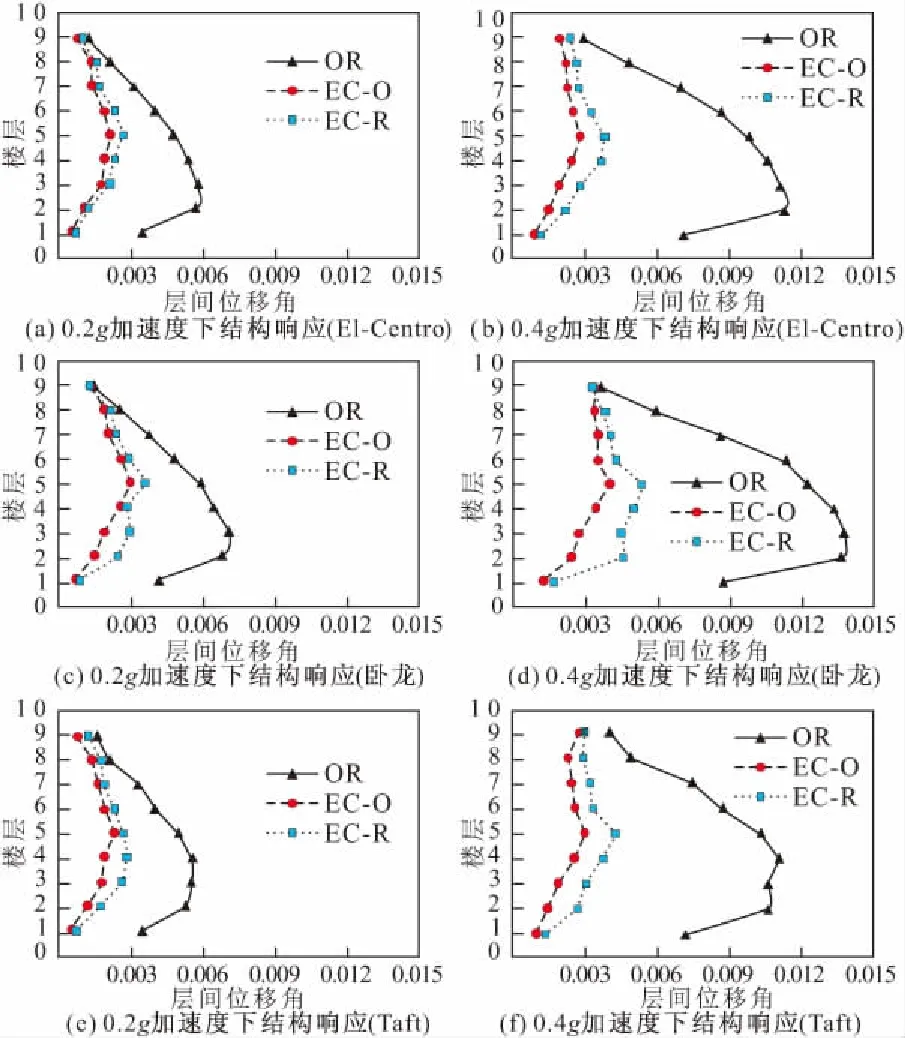
图10 消能结构与原始结构层间位移角比较

(1)如图10a，10b所示，当输入El-Centro地震动，PGA=0.2g时，传统结构的2～6层最大层间位移角均超过1/250的限值[12]，最大出现在第3层为1/172，均进入塑性损伤，而消能结构EC-R的最大层间位移角为1/376，EC-O的最大层间位移角为1/466，均出现在结构第5层，即大部分梁、柱构件保持弹性，阻尼墙开始耗能，说明中震工况下结构基本完好；当PGA=0.4g时，传统结构第2层为薄弱层，层间位移角最大为1/88，而消能结构EC-R的最大层间位移角为1/257，EC-O的最大层间位移角为1/350，均出现在结构第5层。可见，矩形软钢阻尼墙中震工况可减小结构54.3%的最大层间位移角，大震工况可减小结构65.8%的最大层间位移角，而优化型的软钢阻尼墙可以在矩形阻尼墙的减震控制效果基础上，分别对中震和大震工况提升19.3%和26.6%的变形控制能力。

(2)如图10c，10d所示，当输入卧龙地震动，PGA=0.2g时，传统结构的2～6层最大层间位移角均超过1/250的限值[9]，均进入塑性损伤，最大出现在第3层为1/140，而消能结构EC-R的最大层间位移角为1/280，EC-O的最大层间位移角为1/340，均出现在第5层，即大部分梁、柱构件保持弹性，阻尼墙开始耗能，说明中震工况下结构基本完好；当PGA=0.4g时，传统结构第3层为薄弱层，层间位移角最大为1/72，而消能结构EC-R的最大层间位移角为1/191，EC-O的最大层间位移角为1/251，均出现在结构第5层。可见，矩形软钢阻尼墙中震工况可减小结构50%的最大层间位移角，大震工况可减小结构62.3%的最大层间位移角，而优化型的软钢阻尼墙可以在矩形阻尼墙的减震控制效果基础上，分别对中震和大震工况提升17.6%和23.9%的变形控制能力。

(3)如图10e，10f所示，当输入Taft地震动，PGA=0.2g时，传统结构的2～6层最大层间位移角均超过1/250的限值[9]，均进入塑性损伤，最大出现在第4层为1/180，而消能结构EC-R的最大层间位移角出现在第4层为1/354，EC-O的最大层间位移角出现在第5层为1/426，即大部分梁、柱构件保持弹性，阻尼墙开始耗能，说明中震工况下结构基本完好；当PGA=0.4g时，传统结构第4层为薄弱层，层间位移角最大为1/90，而消能结构EC-R的最大层间位移角为1/235，EC-O的最大层间位移角为1/336，均出现在结构第5层。可见，矩形软钢阻尼墙中震工况可减小结构49.2%的最大层间位移角，大震工况可减小结构61.7%的最大层间位移角，而优化型的软钢阻尼墙可以在矩形阻尼墙的减震控制效果基础上，分别对中震和大震工况提升16.9%和30.1%的变形控制能力。

4 结 论

本文针对矩形软钢阻尼墙进行形状优化，给出设计公式，通过有限元软件进行数值仿真分析，得到如下结论：

(1)通过设计公式与有限元计算结果对比，本文给出的矩形阻尼墙设计公式与有限元误差在2%左右，验证了公式的准确性。进一步讨论了优化型阻尼墙的承载力修正系数α，本文数值模拟结果表明α接近1.25。

(2)数值仿真分析表明，本文优化的装配式软钢阻尼墙明显缓解了应力集中现象，减少了80%以上的累积塑性应变，能够最多增加30%的耗能，而且延性更好，在大位移下仍能良好的工作。

(3)矩形阻尼墙中震工况可最多减小结构54.3%的最大层间位移角，大震工况可减小结构65.8%的最大层间位移角，而优化型的软钢阻尼墙可以在矩形阻尼墙的减震控制效果基础上，分别对中震和大震工况最多提升19.3%和30.1%的变形控制能力。

(4)基于装配式思想设计的阻尼墙可有效避免焊接热应力的影响，震后可对损伤的阻尼墙快速拆装，便于提高结构的震后功能恢复能力。而且，装配式构造可以适用于钢结构后期加固改造或者提高抗震设防烈度，亦可以缩小尺寸用于位移较大的结构位置，如核心筒连梁、梁柱节点附近。