纤维增强复合材料结构的层间和层内损伤分析
2017-01-03撰文中国航空综合技术研究所刘秦智
撰文/中国航空综合技术研究所 刘秦智
纤维增强复合材料结构的层间和层内损伤分析
撰文/中国航空综合技术研究所 刘秦智
本文介绍了一种针对纤维增强复合材料结构的高级损伤分析的解决方案,该方法包含成熟的复合材料结构层间和层内损伤的材料模型和判据,能够针对铺层的损伤失效模式进行分析。本文首先介绍了复材层间和层内损伤模型,然后通过对一个标准复材曲梁进行虚拟的四点弯曲试验,验证了所应用方法的准确性。
一、引言
在复合材料结构分析中最主要的挑战就是需要预测它们的损伤失效行为。复合材料主要的损伤失效模式包含层间失效和层内失效。层间失效指相邻层之间的分离,这种现象出现在开孔,厚度过渡区和自由边附近,也较多出现在应力集中状态区域。为了模拟层间失效模式,需要采用特殊的断裂力学方法及粘接单元方法。层内失效包含纤维断裂、基体破坏和纤维与基体的脱离三种不同的失效模式,可以用经典的校核准则如:Tsai-HiⅡ,Tsai-Wu及Puck等做一些简单分析。如果需要分析层内失效及裂纹扩展的过程,还需要特殊的非线性损伤模型和判据。
本文首先介绍了经典的层间和层内失效的模型及判据,然后以复合材料曲梁四点弯曲为例,研究层间失效和层内失效的建模和分析方法,并将分析结果与试验结果进行比对。
二、层间失效模型
对于层间失效的分析,包含断裂力学分析方法和粘接单元分析方法,相比较而言粘接单元方法既能分析复合材料结构是否会发生分层破坏,而且能模拟整个层间失效和裂纹扩展的过程,因此是一种更加常用的方法。粘接单元方法是在层与层之间添加粘接单元,定义粘接单元相关的模型属性,并基于文献1所提到的理论来进行层间失效的分析。该理论中包含三个损伤变量dⅠ, dⅡ和dⅢ,分别代表Ⅰ型、Ⅱ型和Ⅲ型三种不同的层间失效模式。
层间失效的理论判据如下:
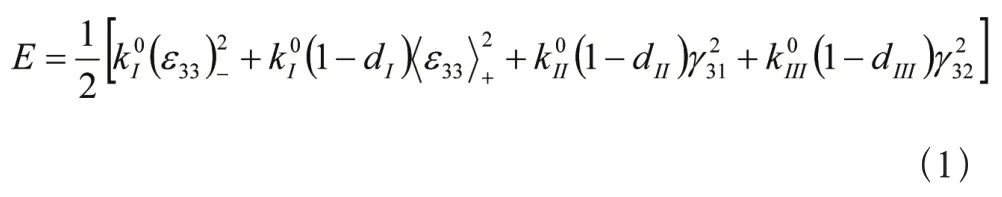
k0
Ⅰ为非损伤刚度。与之相对应的粘接单元模型本构关系如下:
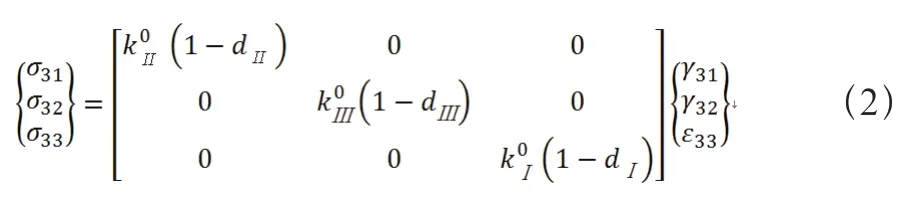
损伤广义力Y可以通过关于dⅠ的表达式(1)推导得出。对于多向加载的情况,层间损伤的演化为与三个层间断裂韧性GⅠC,GⅡC和GⅡC有关,这三个变量分别对应三种不同的层间失效模式,分别为张开型(Ⅰ型)、滑开型(Ⅱ型)和撕开型(Ⅲ型)。等效的损伤广义力Y表示为:
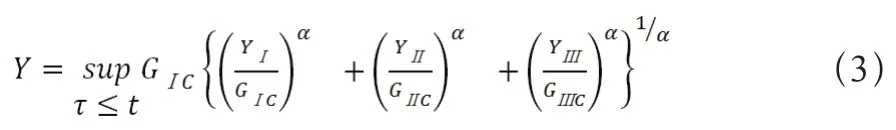
在结构加载中,上述的三个损伤变量有相同演化过程,所以通过设置一个损伤变量d就可以对分层损伤进行模拟。这个损伤变量d与损伤广义力Y相关,分别有三种不同的粘性法则,如图1所示指数型,三角形型,多项式型)。在第4节的数值分析中会用到指数型粘接单元法则。
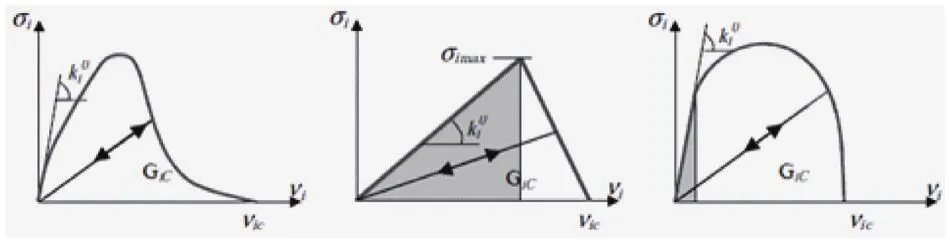
图1 常用的三类粘性法则
三、层内损伤模型
层内损伤模型在文献2中提出,对于层内损伤分析,相关判据如下:

对应模型本构关系中的柔度矩阵如下式:

上式中,d11, d22和d12分别为纤维损伤、横向损伤及剪切损伤所对应的变量。参数λ是面外损伤的表征量:如果其值为空,则损伤不会与第三个方向上的应力相关联。
由此判据得出,并能够通过一些表达式控制层内损伤的演变,如d11= g11(Y11), d22=g22(Y12,Y22),d12= g12(Y12,Y22)。层内损伤也可以定义一个延迟,在损伤发生的时候引用。另外层内损伤不但在纤维方向需要考虑非线性,也需要在层内损伤和裂纹扩展的过程中考虑基体塑性变形对损伤的影响。
四、案例应用
1.应用介绍
下面以复合材料曲梁四点弯曲试验为例,使用复合材料分析软件Samcef来研究层间和层内失效的特性。试样基于ASTM norm6415的测试方法,如图2所示。在此四点弯曲测试案例分析中,需要考虑以下几个方面。
(1)大位移。
(2)上下支撑与样件之间的接触。
(3)双线性材料属性(受拉和受压的杨氏模量不同)。
(4)层间和层内损伤。
如图3所示,通过上下支撑对部件施加载荷。下支撑是固定的。在实验测试时,上部支撑是可以向下移动的,力也可测。这个测试装置在有限元模型中进行了适当简化,在曲梁与支撑的圆柱体间使用了刚柔接触。
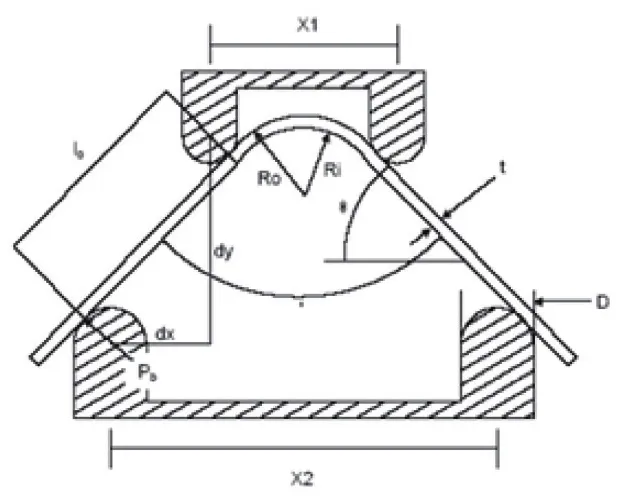
图2 四点弯曲试验

图3 试验后截面图像
复合材料铺层采用四边形膜单元建模,模型规模度达到116208个自由度。在厚度方向上定义了22层,铺层的方向为45°/-45°。在一些层之间,定义了粘接单元,有限元模型中粘连单元层的位置根据试验结果选定,如图3所示。粘连层的位置位于10-11,12-13,15-16,18-19和21-22各层间。
如图3所示,在曲梁的横截面中,各层厚度是不均匀的,尤其是在弯曲的区域。这种厚度的变化在模型中应该被考虑到,因为他对弯曲刚度和结构失效行为有影响。粘接单元的特性可以从参考资料Brauner C和SAMCEF中查到。
2.层内损伤分析
在第一个分析中,我们先忽略层间损伤。从分析结果可以看出,厚度的变化导致分层由一层到另一层的跳变。这点可以通过最大层间正应力点的变化解释。对于仅受作用力矩的曲梁,在其弯曲半径的中间位置有最大层间正应力。有不同厚度的曲梁在其弯曲区域存在一个初始横向位移,因为上支撑的一个圆柱体会首先与曲梁接触。这样,对于曲梁外部的对称载荷就不存在了,而曲梁所经受的也不再是纯弯矩。额外的作用力会在偏心开始出现时产生一个最大剪应力。层间正应力分布如图4所示。

图4 失效前后层间正应力分布
从一层到另一层的分层跳变意味着在层间也存在一些损伤。因为层间失效能够渗透进层内,这种情况可能是基质失效或纤维失效。在图3中,可以看到裂纹从一层跳变到另一层,穿越了其所存在的那一层。一些基质的裂纹意味着结构不会突然失效,但是这却改变了结构的刚度。为了考虑这种物理效应,需要考虑层间损伤模型。
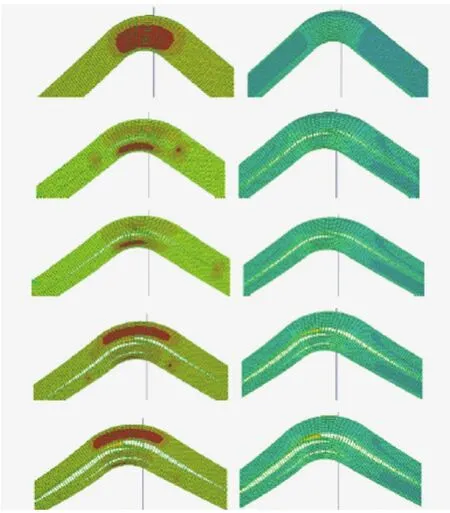
图5 层间正应力(左图)和层间损伤(右图)
3.层间及层内失效的耦合分析
第二个分析使用了层间和层内失效的耦合分析,使5个粘连层的层间失效与层内失效相耦合。在图5中,可以看到对应于位移的正应力和层间损伤。裂纹在第12与第13层之间的接口层开始扩展,与上支撑位置产生了3mm位移。在这个第一个裂纹出现后,整个结构刚度退化。10~11层与15~16层的这一点分层开始体现,并导致了快速损伤。在分析最后,在18~19层的连接处出现了更多分层。力-位移曲线可以找出结构失去其初始刚度时的点。在曲线的前一部分,载荷在位移0.7mm之前都为零值。这主要由于曲梁的不对称性。当曲梁快速失效后,力-位移曲线上可以看到一种变弱的特性。与试验对比,在最大受力处数值结果与试验结果存在3%的差值。上支撑测量的力-位移曲线如图6所示。
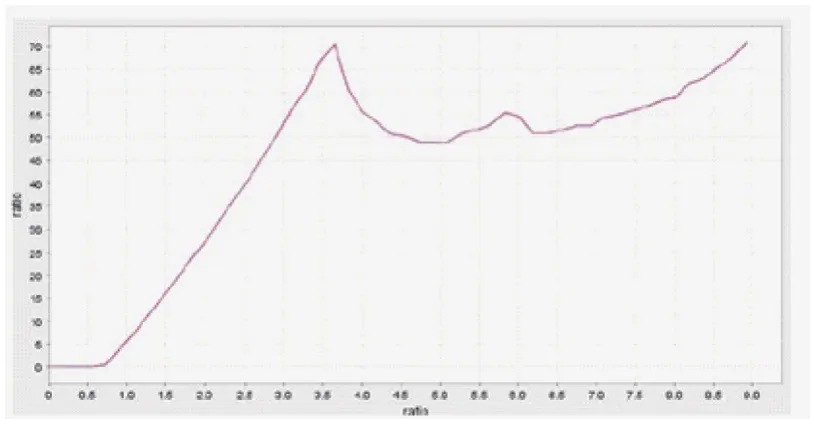
图6 在上支撑测量的力-位移曲线
在图7中显示了层内及层间失效的相互影响。层内失效在位移3.5mm处时开始产生(图7)。左侧图片显示出在层内失效开始时的分层损伤。在红色的单元内,由于层间损伤使刚度减小了42%。在图7右图是仿真最终的损伤状况,颜色已经改变,红色区域已经完全没有刚度。
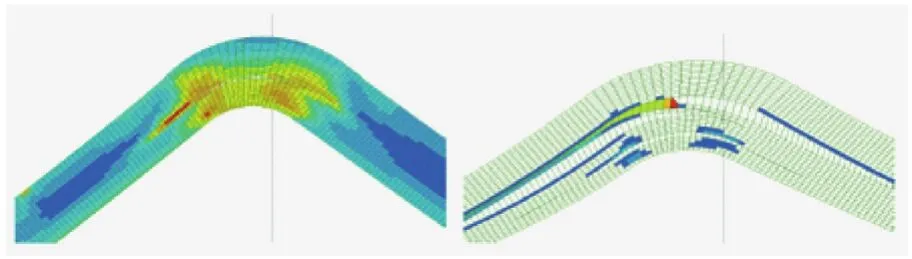
图7 层内失效开始(左图)和层内最终损伤(右图)
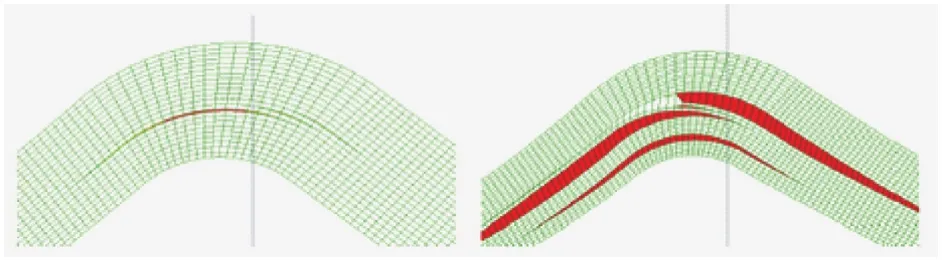
图8 层间失效开始(左图)和层间最终损伤(右图)
在此模型中,层间失效和层内失效同时发生,并且在裂纹尖端存在着相互耦合的效应,这证实了之前的假设,从一层到另一层的分层跳变会对跳变穿过的层的特性产生一定影响。在力-位移的曲线(图6)中,在部件整个失效前刚度存在一个较小的变化。
五、结语
本文基于Samcef复合材料分析软件对复合材料结构的渐进损伤进行分析,在分析中考虑几何非线性、材料非线性以及接触、摩擦等非线性条件。同时还考虑了层间损伤和层内损伤的耦合效应。基于复合材料层间和层内损伤的模型和判据,对比四点弯曲试验结果,验证了复材结构损伤中的各种非线性的影响。
