软土场地上双座串联大跨度斜拉桥地震响应及碰撞分析
2020-07-21王德光沈文爱何友娣
王德光,王 恒,沈文爱,何友娣,张 强
(1. 杭州江东建设工程项目管理有限公司,浙江 杭州 310004;2. 华中科技大学 土木工程与力学学院,湖北 武汉 430074;3. 中铁大桥勘测设计院集团有限公司,湖北 武汉 430050)
在近几年国内外桥梁建设中,由于斜拉桥具有造型美观、结构受力合理、跨越能力大、施工方便等优点[1],其应用日益广泛。而随着全球地震活动频繁发生,作为交通运输枢纽的斜拉桥一旦破坏,将造成巨大的经济损失及安全问题,因此,斜拉桥的地震响应研究得到了人们的重视。
目前,国内外针对斜拉桥地震响应的研究主要集中于桥梁结构体系[2,3]、地震动分析方法[4~6]及减隔振装置[3,7,8]等方面。文献[9]以某塔梁固结的独塔斜拉桥为研究对象,通过模型试验和数值模拟,研究了其受力状态、极限承载力及传力机理。文献[10]以某半漂浮体系双塔斜拉桥为背景,探讨了E型钢阻尼器和液体粘滞阻尼器的布置方案及减震限位效果。文献[11]基于非线性有限元理论,对刚构体系斜拉桥的地震响应特点进行了研究。文献[12]针对桥梁的塔梁固结体系、漂浮体系、半漂浮体系,以泰州长江公路大桥为对象,对跨中最大挠度和主缆抗滑移系数影响因素进行分析。可以看出,多数文献重点在于不同桥型、塔梁连接方式对斜拉桥地震响应的影响研究[13~16]。双座串联斜拉桥是大跨度斜拉桥设计实践中的一种创新,目前针对这一类型斜拉桥的地震响应及其减震措施的研究还未见报道。为丰富斜拉桥地震响应研究内容并为类似待建桥梁提供一定的理论基础及指导意义,本文以软土场地上串联大跨度斜拉桥——洪鹤大桥为背景展开研究。
全文组织结构如下:首先,基于Midas模型,对桥梁进行动力特性分析;随后,选取合适的地震波,以纵桥向+0.3横桥向+0.3竖桥向的激励组合方式输入,采用非线性时程分析法,对结构关键部位的位移、内力进行计算和分析,并将结果与反应谱法进行对比;最后,针对桥梁的串联特性,对交接墩处主梁的碰撞问题进行研究,并对其提出合理的减震限位措施。
1 工程概况及动力分析模型
1.1 工程概况
洪鹤大桥桥长9.654 km,起点位于珠海市香洲区南屏镇洪湾,衔接洪湾互通,与广珠西线及横琴二桥、港珠澳大桥连通,终点与正在建设的鹤港高速公路、规划的金海大桥连接。两座主航道桥均为桥跨布置为73+162+500+162+73 m的双塔双索面叠合梁斜拉桥,全长970 m,半漂浮体系,总体布置如图1所示。主塔采用钻石型钢筋混凝土桥塔,辅助墩和边墩采用独柱墩。主梁采用开口叠合梁形式,总长970 m,钢梁部分包括纵梁、横梁、小纵梁、压重箱及过渡梁、锚拉板、钢锚梁、钢牛腿及预埋件等组成。斜拉索采用镀锌钢绞线拉索,两桥均有160根索。钢主梁采用Q370QB,桥面板采用26 cm厚C60混凝土,主塔采用C50混凝土。
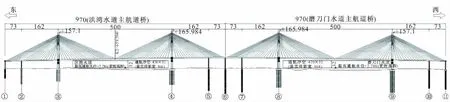
图1 洪鹤大桥总体布置/m
1.2 Midas模型
本文采用Midas Civil软件建立洪鹤大桥有限元模型,如图2所示。斜拉索采用桁架单元模拟,桥塔、钢主梁、桥墩、承台以及桩均采用梁单元模拟,桥面板采用板单元模拟。考虑桩-土-结构相互作用的影响,桩土互相作用采用等效土弹簧模拟,弹簧刚度系数由m法计算得到,土质情况参考《洪鹤大桥详勘工程地质勘察报告》。通过约束桥塔与主梁、桥墩与主梁之间的竖向自由度模拟球形支座。用一般连接中的滞后系统模型模拟桥墩与主梁间的横向C型钢阻尼器,其系统如图3所示(方框内为恢复力模型,d为N1,N2两节点的相对变形,f为出力)。C型钢阻尼器参数见表1,示意图如图4。两座主梁之间设置20 cm间距的抗震缝。

图2 洪鹤大桥Midas模型

图3 C型钢阻尼器的力-位移滞回模型

表1 C型钢阻尼器参数
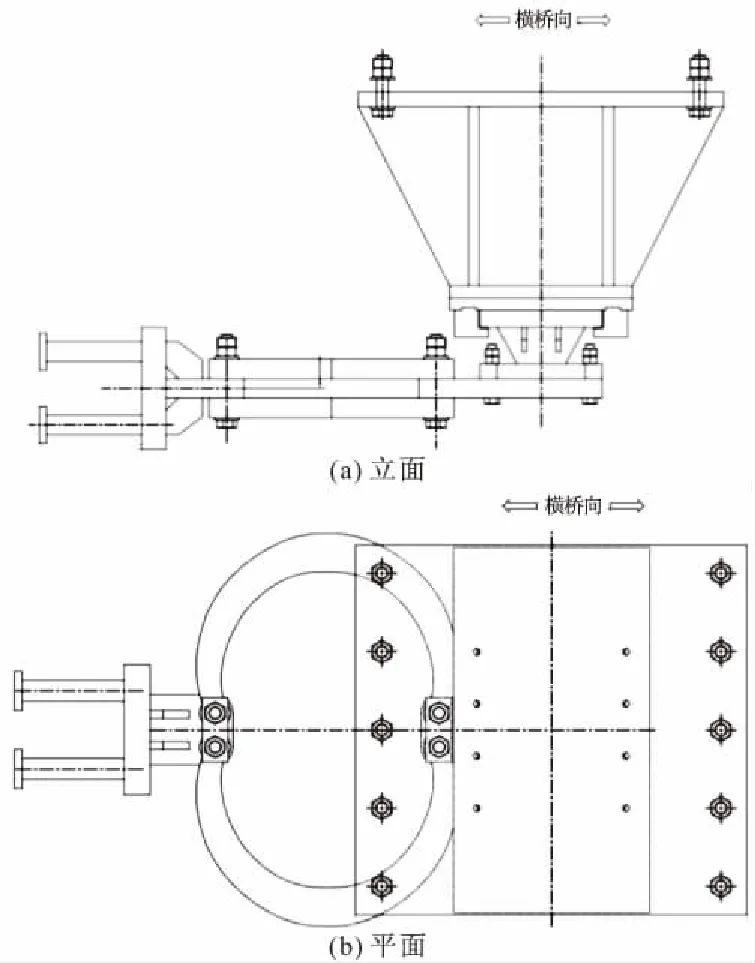
图4 C型钢阻尼器
1.3 动力特性分析
利用Midas Civil程序中的多重Ritz向量法计算模型的动力特性,结果如表2所示。可以看出,结构的基频为0.099 Hz,基本周期为10.10 ,属于长周期结构。主桥的1,2阶振型为两主梁的顺桥向纵漂,符合半漂浮体系的特征。3~6阶出现主梁的侧弯,说明主梁横向刚度小于竖向刚度。前10阶自振频率分布在0.099~0.306 Hz之间,因此在外荷载作用下,易激发多个低阶振型,应引起重视。图5为结构在平动方向的振型有效质量占总质量的百分比随振型模态阶数变化的情况。可以看出,用振型反应谱法计算结构响应时,考虑前300阶振型可满足JTG/T B02-01—2008《公路桥梁抗震设计细则》[17]的规定。
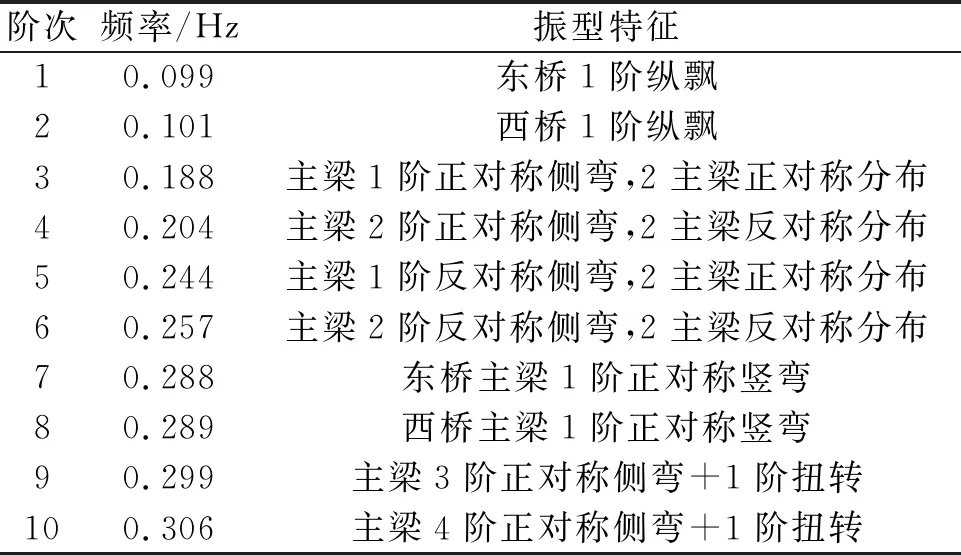
表2 洪鹤大桥动力特性
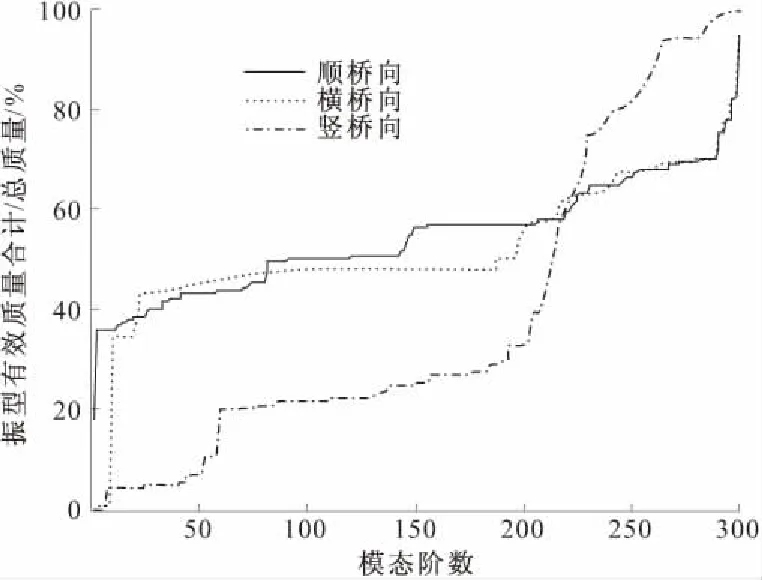
图5 振型有效质量统计
2 地震响应分析
2.1 地震动输入
地震动输入是影响地震响应时程分析的重要因素之一。选取地震波必须满足地震动三要素:持时、峰值、频谱特性,否则结构的地震响应分析可能就不具有参考意义。本文采用《洪鹤大桥工程场地地震安全性评估报告》提供的满足桥址场地条件要求及抗震设计的3条人工波进行地震响应分析,取响应的最大值作为桥梁地震反应的结果。人工波由该斜拉桥场地50年超越概率为2.5%的地表水平向设计地震动加速度反应谱生成(E2地震作用,峰值为0.503g)。人工波的持时为40.94 s,采样频率为50 Hz,时间间隔为0.02 s,小于结构基本周期的1/50,满足计算精度要求。图6~8为3条地震波的加速度时程曲线,为方便后文时程分析方法中瑞雷阻尼的参数选取,同时给出了3条时程曲线的频谱图。此外,3条人工地震波的加速度反应谱与设计反应谱的对比如图9所示,由图可以看出,人工地震波反应谱与地震设计反应谱拟合很好,能准确反映出地震动的特性。
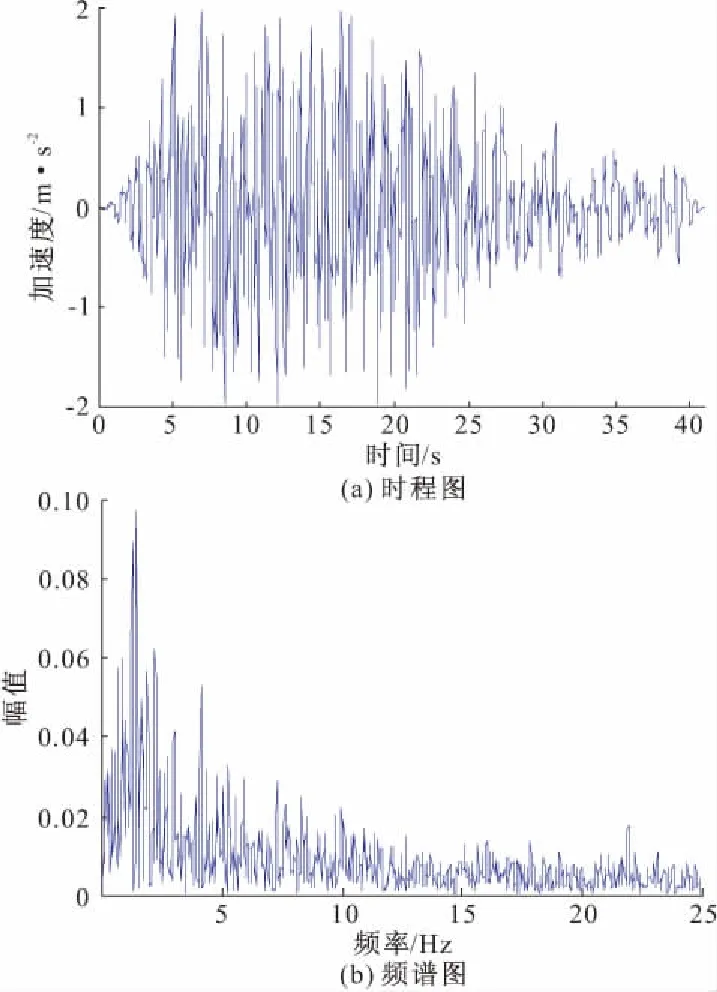
图6 E2地震作用人工地震波1的加速度时程图和频谱
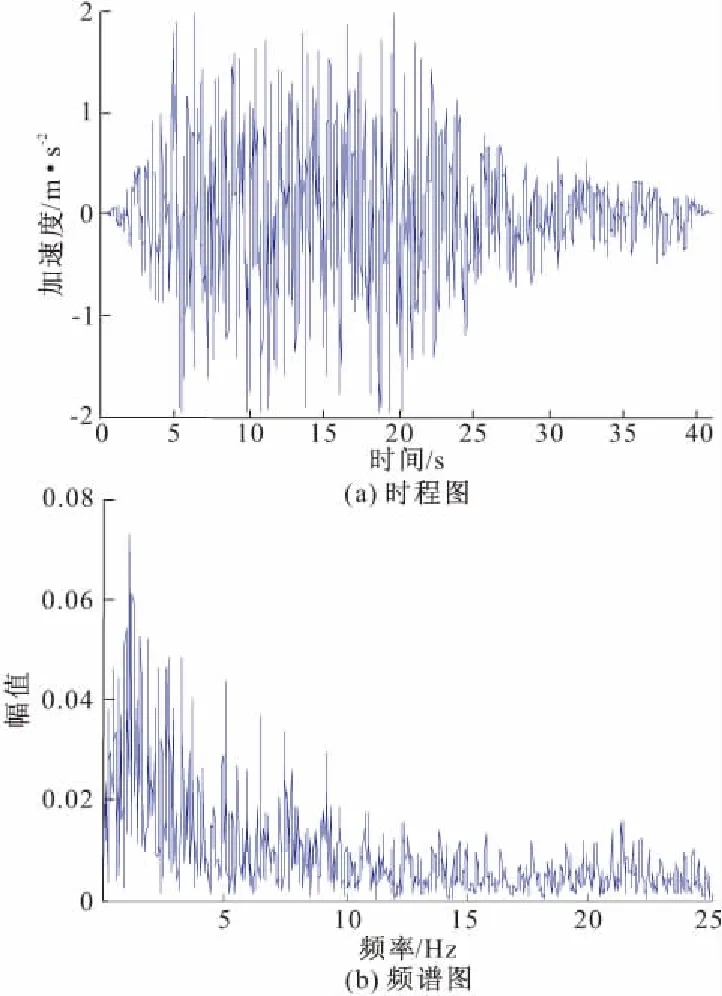
图7 E2地震作用人工地震波2的加速度时程图和频谱
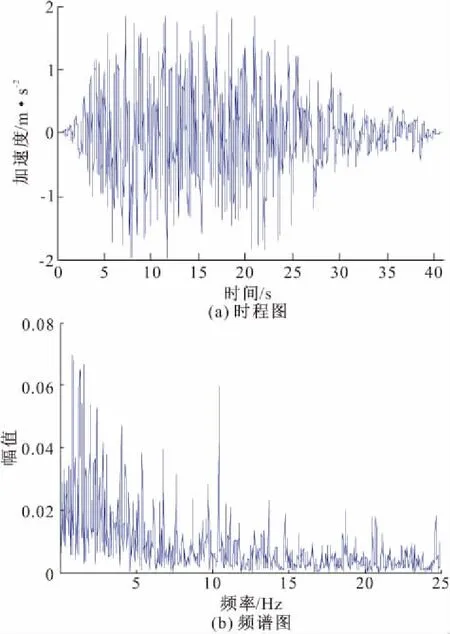
图8 E2地震作用人工地震波3的加速度时程图和频谱
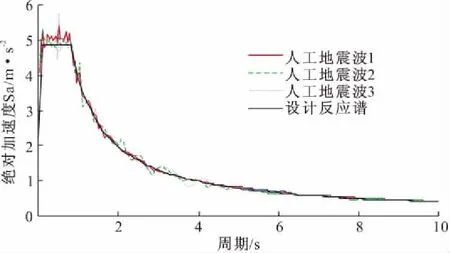
图9 人工地震波反应谱与设计反应谱对比
2.2 关键部位的位移与内力分析
由于大跨度斜拉桥具有明显的空间特征,因此进行地震响应分析时应当同时考虑纵桥向x、横桥向y和竖桥向z的地震作用,本文采用非线性时程分析法研究了3个方向地震作用下桥梁的动力响应,即顺桥向(x向)+0.3横桥向(y向)+0.3竖桥向(z向)地震作用(Ex+0.3Ey+0.3Ez)。时程分析采用瑞雷阻尼,阻尼频率点的选取根据地震作用的频率成分和结构本身的动力特性综合考虑。位移响应方面,以主塔塔顶位移和1号梁(东桥主梁)梁端位移、2号梁(西桥主梁)梁端位移为研究重点。内力响应方面,以各墩底、塔底的剪力和弯矩为研究重点。同时,将结果与反应谱法进行对比,获得更全面的分析。反应谱法计算考虑前300阶模态的贡献。图10与表3中的时程分析结果为3条地震波作用下响应的最大值。

图10 时程分析法和反应谱法位移响应结果对比
图10为两种方法在主塔和梁端的位移响应计算结果,可以看出,二者吻合较好。由图10a~10c可知,各主塔塔顶的位移主要以纵桥向为主,均在1.2~1.3 m之间,横桥向、竖桥向位移很小,尤其竖桥向位移,均不足1 cm。由图10d~10f可得,两个主梁纵桥向位移较大,均在1.1 m左右,而横桥向也发生不可忽略的位移,最大达20 cm,应引起重视。此外,主塔、主梁的位移响应不仅与地震激励有关,还与约束条件及桥梁动力特性有关。
两种计算方法下各截面内力响应绝对值如表3所示,括号内为反应谱法计算结果。二者存在较大的区别,有少量截面处误差达到50%以上。原因在于:地震加速度反应谱是通过统计平均所得,反应谱所求的响应具有“统计意义”;而时程分析法是利用某条地震波进行计算,所得响应受样本地震波特性控制,因此二者可能存在较大的内力误差。但为安全评估结构的内力情况并作出合理的抗震设计,应将二者结合,综合考虑以得到合理的结果。
限于篇幅,以y表示截面横桥向,z表示截面竖桥向。由表3可看出,y剪力最大值、z弯矩最大值发生在4号塔底右边,分别为22953 kN,516251 kN·m,z剪力最大值和y弯矩的最大值发生在8号塔底右边,分别为19763 kN,1739229 kN·m。同时,主塔塔底的内力均远大于各个墩底的内力。因此,在抗震设计中,应注意这些截面的抗剪及抗弯性能。
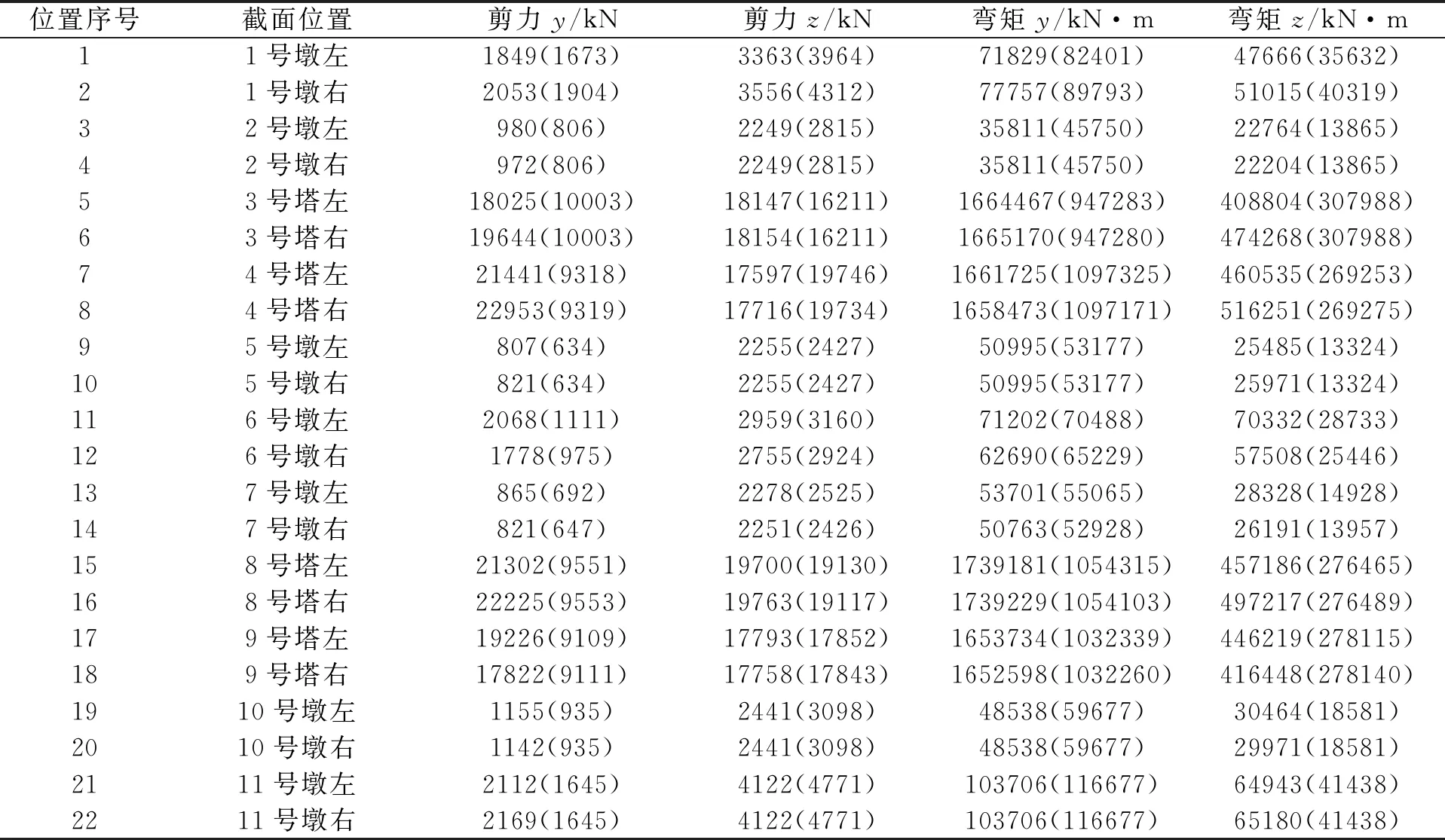
表3 时程分析法和反应谱法内力计算结果
3 交接墩处主梁碰撞分析
3.1 交接墩处梁端位移响应分析
双座串联斜拉桥在交接墩处的碰撞问题是抗震分析的重点之一。图11为交接墩处局部详图。图12为在人工波1的激励下,梁端的位移响应和加速度响应。可以看出,一致激励下,1,2号梁的运动并不会出现明显的滞后现象,为更直观地观察,图13a对比了二者的位移响应时程。由于2主梁的间距仅为20 cm,因此需要加以计算分析才能判定是否发生碰撞。1,2号梁的运动情况分为3种:(1)二者同时同向运动;(2)二者同时朝向交接墩中心运动;(3)二者同时背向交接墩中心运动。前两种情况均有碰撞的可能,利用Matlab软件将二者梁端间距变化计算得出。由图13b可知,整个激励过程中,梁端间距最大为38.53 cm,最小为3.79 cm。三条地震波下梁端间距最小值是在1号地震波作用时出现,此次研究中交接墩处不会发生主梁碰撞的情况。但是仅3条样本地震激励无法完全准确反映实际地震反应,且图中梁端间距有出现小于3.79 cm的趋势,因此有必要进行适当的减震限位措施。图13c,13d为两个主梁梁端的位移响应频谱,其卓越频率均为0.0976 Hz,与结构的基频基本相等,说明二者纵向位移基本是由纵漂振型控制的。
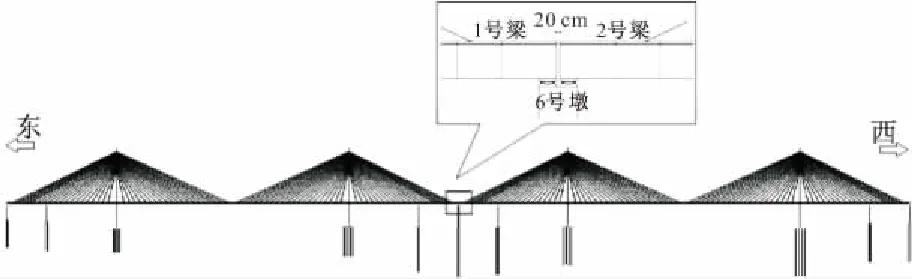
图11 交接墩处局部详图
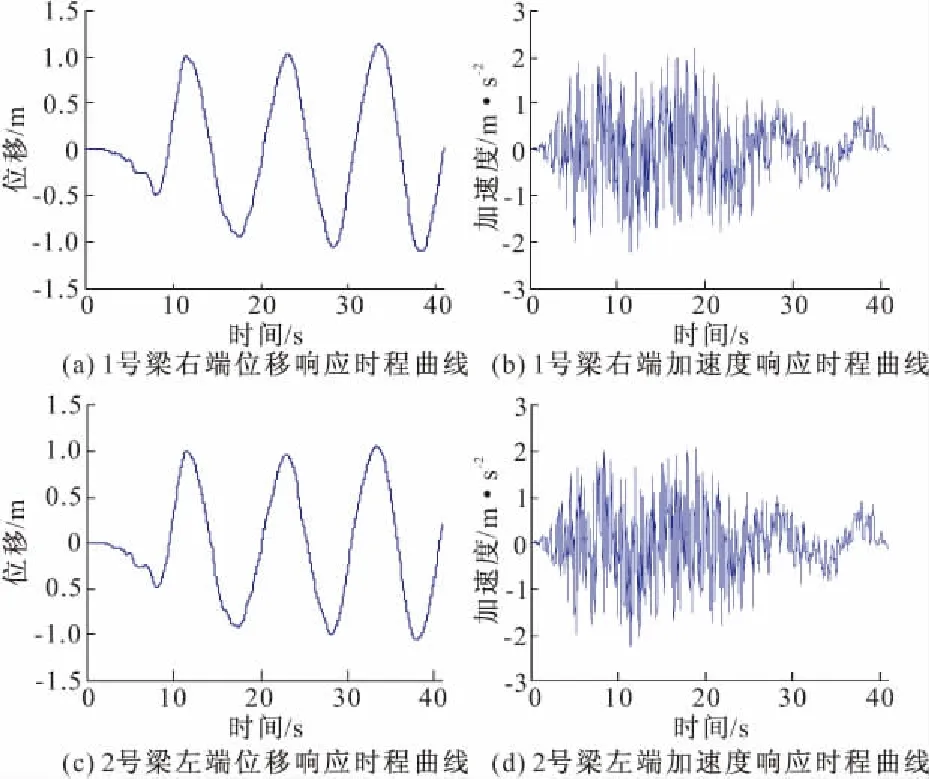
图12 1号人工地震波下梁端位移响应时程曲线
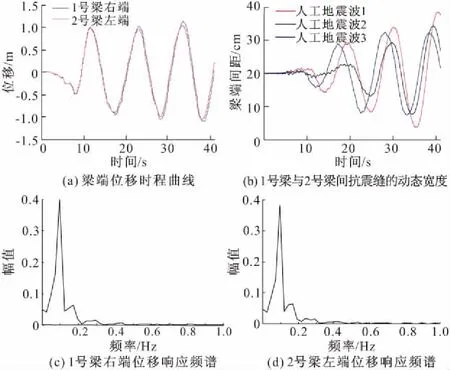
图13 交接墩处梁端位移响应分析
3.2 减震措施
前一小节中得出交接墩处主梁梁端发生碰撞的风险较高,为确保桥梁在强震作用下的安全,现在各个塔梁处布置纵向液体粘滞阻尼器,共8对16个。东侧桥阻尼器平面布置如图14所示,西侧桥与其一致。

图14 阻尼器布置
纵向液体粘滞阻尼器的阻尼力表达式为:
F=CVα
(1)
式中:F为阻尼力;C为阻尼系数;V为相对速度;α为速度指数。从粘滞阻尼器应用于桥梁抗震的角度来讲[18],C的范围一般为1000~10000 kN/(m/s)α,α的范围一般为0.2~1。本文在Midas软件中用Maxwell模型来模拟液体粘滞阻尼器,力学模型如图15所示(Cd为阻尼系数,Kb为弹簧刚度系数,dd,db分别为阻尼器和弹簧的变形量,f为出力)。其中,弹簧单元取值1×107kN/m,以模拟刚性连接。阻尼单元取值见表4。

图15 液体粘滞阻尼器Maxwell力学模型

表4 纵向液体粘滞阻尼器参数
从图16中可以看出,布置纵向液体粘滞阻尼器后,1号梁右端、2号梁左端的纵向位移响应峰值均减小超过40%。在梁端间距方面,图17为1号梁与2号梁间抗震缝的动态宽度变化情况,其最小值为17.08 cm,远大于不安装液体粘滞阻尼器时对应的间距。因此,在该桥梁塔梁处设置液体粘滞阻尼器减震限位效果明显。

图16 有无阻尼器位移响应峰值对比
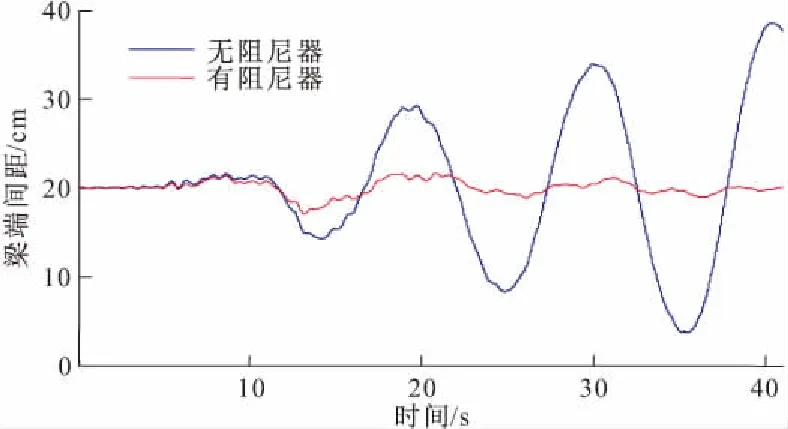
图17 1号梁与2号梁间抗震缝的动态宽度
4 结论与展望
本文以广东珠海市洪鹤大桥为对象,研究了E2地震作用下双座串联大跨度斜拉桥的内力和位移响应。研究结论如下:
(1)本桥梁为半漂浮体系,第一阶振型为纵漂。桥梁的基本周期为10.11 s,属于长周期结构,对减小地震作用是有利的。但主梁纵漂会使得塔顶、梁端产生较大位移,应引起重视。桥梁的横向刚度较弱,此方向的抗弯刚度设计也应考虑。
(2)在纵桥向+0.3横桥向+0.3竖桥向地震激励组合下,主塔塔顶、主梁以纵向位移为主,且位移均大于1 m,应考虑设置纵向阻尼器进行减震限位。同时,主梁横向位移不容忽视。内力方面,各主塔底处的剪力、弯矩均大于各墩底,其中,4号塔塔底右边、8号塔塔底右边尤为突出,因此对该截面抗剪、抗弯应重点关注。
(3)在交接墩处,3条人工地震波激励下,1号梁右端和2号梁左端具有发生碰撞的风险。因此,需在塔梁处布置纵向阻尼器加以控制。当采用液体粘滞阻尼器进行纵向减震控制时,结果表明其位移响应峰值减震率达40%以上,可十分有效地防止两座串联的斜拉桥在E2地震作用下发生碰撞。
