被动桩-侧移软土相互作用与桩身被动荷载分析

张 浩，孙 凯，杨 玲，郭院成

(1. 郑州大学 土木工程学院, 河南 郑州 450001；2. 郑州市市政工程管理处,河南 郑州 450053；3. 郑州市市政设施维修建设有限公司, 河南 郑州 450053)

工程实践中，引起周围土体相对桩体发生运移的诱因很多，如坡体滑坡、临近堆载或开挖等[1]，使得既有构筑物基础桩基在主动承担结构荷载的同时，还需要抵抗周围土体位移所产生的被动荷载作用。尤其是在饱和软黏土中，土体侧向位移对桩身产生的附加水平荷载，极易使基桩的承载性状发生明显改变。原本按抗压承载和沉降控制设计的竖向承载桩，可能转变为受水平附加被动荷载控制的侧向抗弯桩。若考虑不当，极易产生工程问题，如2009年上海“莲花河畔景苑”一幢13层楼房的整体倾覆事故[2]、连云港某互通因下行公路路基填筑引起跨线桥60根墩柱偏移事故[3]等。

因此，科学评估侧移土体与被动受荷桩之间的相互作用以合理确定桩身附加被动荷载效应成为解决此类工程问题的关键。目前，我国现行设计规范中尚无针对桩周土体侧移不利影响的充分考虑。国内外学者们大多采用数值分析的方法对此类被动桩的桩土相互作用与受力特性进行研究[2,4～6]。简化的理论分析方法则分别从变形协调和作用等效两个角度入手开展了大量研究，并形成了基于土体位移的两阶段分析法[4～6]和基于土压力的极限作用力模型[7～8]。其中，前者主要是通过数值模拟或现场实测首先确定无桩地基土的侧向位移场，然后将其施加于桩上，根据桩土变形协调确定桩身被动荷载；后者则是根据试验或理论分析，将土体侧移作用等效假定为桩身侧向分布荷载，进而借鉴水平受荷桩分析原理进行计算，更易为工程人员掌握应用。如：Ito等[9]基于塑性变形理论，给出了抗滑桩桩身侧向被动荷载计算公式。

考虑不平衡堆载或边载作用下的既有桩基被动受荷效应，Beer等[10,11]针对临近路堤荷载作用工况，提出桩身被动荷载呈矩形与三角形分布的半经验公式；为了进一步揭示位移土体与被动桩的相互作用，竺明星等[12]将Ito塑性变形理论模型引入到堆载作用下隔离桩的被动荷载分析中，提出了改进的桩身极限被动受荷计算方法；张浩等[13]通过修正Ito塑性变形理论模型，并结合沈珠江[14]极限平衡理论，给出了路堤边载作用下既有桩基的被动荷载计算方法。针对桩土相互作用问题，Randolph等[15]基于平面问题假定，对水平受荷桩的桩土相互作用进行了极限理论分析(上下限理论)，给出了主动受荷桩桩身极限阻力的精确解，为合理揭示桩土相互作用提供了基础。然而，这种极限状态下的分析，没有考虑位移土体与桩基相互作用时土体塑性区的开展问题，往往与被动桩的实际受荷情况不符。

据此，本文基于侧移土体与桩相互作用的平面问题假定，采用滑移线塑性理论，构建了桩周土体塑性区不同开展范围时桩身被动荷载的计算模型，并根据力学平衡原理，给出相应计算公式；在此基础之上，分析桩前法向应力与桩周土塑性区开展范围的关系及其变化规律，建立了一种可考虑桩周土塑性区开展的桩身被动荷载简化计算方法，为侧移土体作用下桩身被动荷载的合理确定以及被动桩受力性状分析提供借鉴。

1 模型构建与基本假定

地基土尤其是饱和软黏土，在外部荷载或环境变化时(如堆载等)极易发生侧向位移，进而会对邻近基桩产生侧向附加荷载作用。随着桩土相对位移的增加，桩身附加被动荷载逐渐增大；而与此同时，在桩身抗力作用下，位移软土逐渐达到塑性屈服，且塑性区逐渐开展，直至位移软土沿桩身侧面发生塑性绕流运移[14,15]，桩身附加被动荷载达到极限值。可见，桩周软土塑性区的开展是桩土相互作用的宏观表征。

据此，考虑到位移软土与基桩的相互作用，为简化问题，作以下基本假定：

(1)考虑桩的竖向延展，将侧向桩土相互作用近似看作平面应变问题[4,9,14,15]；

(2)不考虑饱和软土固结排水影响，并将其看作纯黏性土(软土内摩擦角φ≈0)，即符合Tresca屈服准则[14]：

|τf|=c

(1)

(3)考虑桩土界面的摩擦效应，假定桩土界面摩阻力为τa，由图1桩土界面应力莫尔圆可看出：

τa=αc

(2)

(3)

式中：α为桩土界面摩擦力发挥系数。

图1 桩土界面应力莫尔圆

进而，基于极限分析理论，借鉴水平受荷桩桩土相互作用极限模型[15]，可构建桩周土体侧移作用下桩周软土塑性区的滑移线网格。图2所示即为根据对称原理得出的第一象限中桩周软土滑移线场，可将软土塑性区滑移线场划分为：

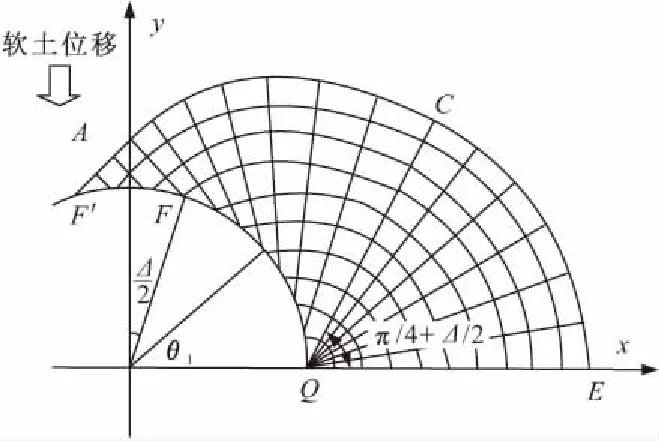
图2 极限状态下软土滑移线网格

(1)刚楔体AFF′：软土位移作用下，因桩身表面的黏附力作用而在桩前形成刚楔体AFF′，该区域内土体黏附于桩身，近似看作刚性体。软土运移作用桩身的主应力方向与y轴平行，由Tresca材料滑移线理论不难得出，该区域土体滑移线与y轴夹角为π/4，而受桩身黏附力影响，桩身表面F点主应力方向发生偏转Δ/2，则滑移线AF与y轴夹角为π/4、与F点法线方向夹角为π/4+Δ/2。并且，根据AF边界应力条件可知，AFF′区域为均匀应力场。

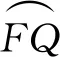
(3)扇形区QCE：该区域土体塑流不受桩身表面黏附力的影响，根据Tresca材料滑移线特征，该区域滑移线场呈扇形分布，如图2所示。

由滑移线理论可知，平面应变条件下土体应力方程的特征线与上述滑移线方向重合，在物理意义上应力特征线即为滑移线[15]。据此，对上述构建的滑移线场进行分析，设塑性区滑移线边界QE处平均应力为σ0，根据滑移线的基本性质，通过桩身界面应力和刚楔边界应力积分，由土体位移方向静力平衡方程，可得位移软土发生绕桩塑流极限状态下桩身的被动极限荷载Pu为：

(4)

式中：d为桩身横截面直径。

2 位移软土塑性区局部开展分析

当软土侧移相对较小时，桩前法向应力相对较小，桩身抗力作用下位移软土可能仅局部出现塑性屈服，但软土位移仍会对桩身产生附加被动荷载。考虑软土受荷弹性变形较小，甚至可忽略不计，该工况下桩身因软土位移而承受的被动荷载主要由桩周软土塑性区的开展程度所决定，即随着桩前软土塑性区的开展，软土位移对桩基的荷载效应逐渐增大，直至桩周软土发生绕桩塑性流动。因此，可将位移软土与桩的相互作用表征为位移软土塑性区的动态开展，通过对塑性区不同开展程度下桩身应力分析，即可得出位移软土作用于桩身的被动荷载。

2.1 桩前塑性区局部开展

当软土侧移相对较小时，位移软土塑性区仅在桩前局部开展，为简化分析，基于位移软土与桩相互作用的平面应变假定，将桩前局部塑性区划分为刚楔体AFF′、渐开区AFBC和三角形刚楔体BCD，如图3所示。由滑移线理论可知，刚楔体AFF′和BCD皆为均匀应力场，进而可推导桩前塑性区局部开展时的桩身被动荷载。

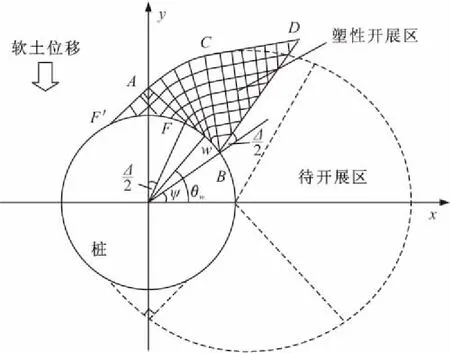
图3 桩前塑性区局部开展模型

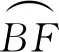
σn,w=c[1+2(θw-ψ)+cosΔ]

(5)

τw=τa=csinΔ

(6)

(7)

桩前刚楔区AFF′，由上述分析可知该区域主应力方向与y轴平行，其上任意点w(π/2-Δ/2<θw≤π/2)的法向应力σ′n,w和切应力τ′w可以表示为：

σ′n,w=c(1+π-2ψ-Δ-cos2θw)

(8)

τ′w=csin2θw

(9)

同理，对边界AF上各点应力积分，可得第一象限刚楔区沿软土位移方向作用于桩上的荷载为：

(10)

联合式(7)和(10)，根据对称原理，可得桩前塑性区局部开展时(0≤ψ<π/2-Δ/2)桩身被动荷载为：

(11)

当π/2-Δ/2≤ψ，即塑性区在刚楔区范围内时，由式(8)和(9)不难得出此时桩身被动荷载为：

Pψ=(2+π-2ψ-Δ)cdcosψ

(12)

2.2 桩侧土塑性区局部开展

随着上述桩前塑性区的进一步开展，当ψ=0时，桩侧扇形区内土体开始发生局部的塑性绕流，此时塑性区的开展主要位于桩侧土体区域。软土塑性区由刚楔体AFF′、渐开区AFBC、扇形区BCE和三角形刚楔体BED四部分组成，如图4所示。

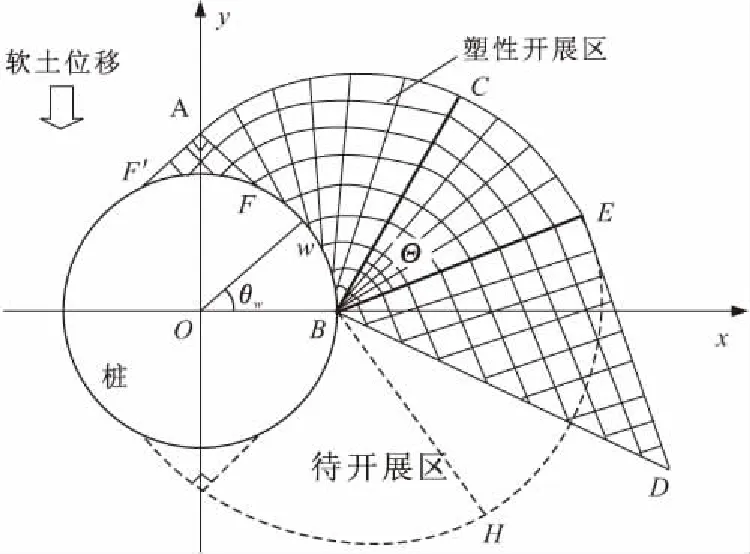
图4 桩侧塑性区局部开展模型

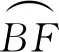
由滑移线理论可得BC线上平均应力为σ=c+2cΘ，以此为初始条件，同上述推导过程可得桩侧土塑性区开展至扇形区时桩身被动荷载为：

(13)

2.3 桩后塑性区局部开展

当桩侧扇形塑流区开展完全后，土体塑性区进一步发展将在桩后对桩基产生影响。据此，构建塑性区开展到桩后土体时的桩土作用模型，如图5所示。

图5 桩后塑性区局部开展模型

σn,i=c[1+2(κ-θi)-cosΔ]

(14)

τi=τa=csinΔ

(15)

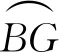
(16)

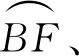
(17)

(18)

根据对称原理，联合式(16)～(18)可得该工况下土体位移方向上桩身被动荷载为：

(19)

由图5可以看出，当κ≥π/2-Δ/2时，土体发生完全绕桩塑流，将κ=π/2-Δ/2代入式(19)所得结果与式(4)完全绕流时极限荷载结果完全一致。

据此，根据式(4)，(11)～(13)，(19)即可对塑性区不同开展程度时桩身被动荷载和完全绕流时桩身极限荷载进行计算分析。

2.4 桩身被动荷载的简化确定方法

基于上述理论模型，对位移土体塑性区不同开展范围时作用于桩身的荷载进行计算分析。基本计算参数：土体不排水抗剪切强度cu=10 kPa，重度γ=15.7 kN/m3；基桩直径d=1.0 m；D1，D2分别为桩间距、桩间净距。计算中，塑性区开展范围由角度Ф表征(由上述推导可知，Ф包含桩前塑性区开展角ψ、桩侧土体塑流开展角Θ和桩后塑性区开展角κ)。

图6所示为桩周位移土不同塑性区开展时桩侧被动受荷情况。可以看出，随着桩周土体塑性区开展角Ф增加，位移土体作用于桩身的附加被动荷载呈近似线性增大趋势，直至土体发生完全绕流的极限荷载，这一规律符合前述被动桩受力机制特征。

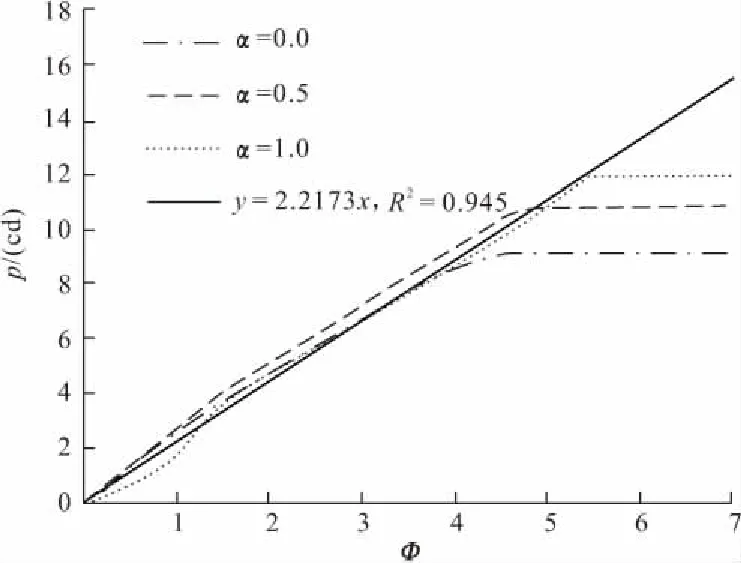
图6 位移土塑性区局部开展时桩身受荷情况

据此，可得桩身土压力值P与桩周土体塑性区开展角度Ф之间的数学表达式为：

P/(cd)=λΦ

(20)

式中：λ为计算系数，如图6可根据具体工况通过计算回归得出。

同理，进一步考察位移土体塑性区不同开展范围时作用于桩前A处的法向应力，如图7所示。可以看出，桩前A处的法向应力σv,A随位移土塑性区开展角Ф呈线性增加的变化趋势。

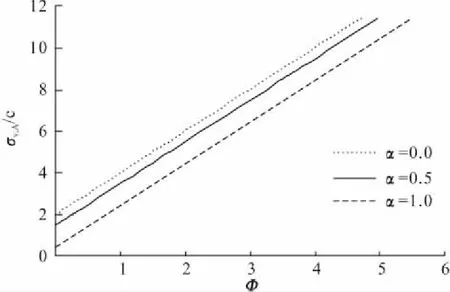
图7 位移土塑性区局部开展时桩前A处法向应力

进而，可得桩前A处法向应力σv,A与桩周土体塑性区开展角度Ф之间的数学表达式为：

σv,A/c=aΦ+b

(21)

式中：a,b为计算系数，如图7可根据具体工况通过计算回归得出。

联合式(20)(21)，可建立桩侧土压力值与桩前法向应力的简化表达式为：

P/(cd)=η(σv,A/c-b)

(22)

式中：η为计算系数，η=λ/a。

其中，桩前法向应力可根据下式求出：

σv,A=σx+K0γz

(23)

式中：σx为桩前A处的水平向附加应力，以堆载作用为例，文献[12,13]基于Boussinesq改进解，根据临近堆载的几何特征给出了水平向附加应力的计算方法；K0为静止土压力系数。

据此，考虑邻近堆载荷载水平，根据不同深度处桩前法向应力(式(23))，由式(22)可近似求出考虑桩周位移土塑性区开展影响的桩侧被动受荷值P；而当P≥Pu时，表明桩周土塑性区完全开展发生绕流，可由式(4)确定P=Pu。

3 验证分析

考虑极限状态下位移土体作用于桩身的侧向压力水平，基于上述方法对桩侧极限土压力值Pu进行计算，并将其与几种常用桩侧极限土压力计算方法计算结果进行对比，如图8所示。

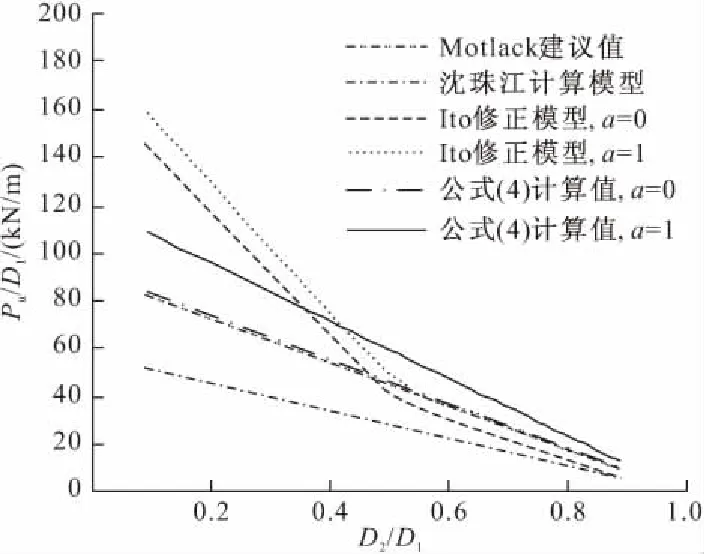
图8 桩侧极限土压力计算结果

可以看出，由本文式(4)计算的桩侧极限土压力值与Matlock[16]软黏土极限土压力建议值较为接近，尤其当桩身完全光滑(α=0)时计算值与建议值基本吻合；但与沈珠江计算模型[14]计算值相比，本文式(4)计算值相对较大，这主要是因为沈珠江院士所提出的计算模型是基于极限平衡理论，属于极限分析下限解，小于土体绕流时的实际极限作用力；张浩等[13]考虑了排桩桩前土拱效应和桩后绕流影响，并建立Ito修正模型，其计算值与式(4)计算结果较为接近，当桩身完全光滑(α=0)和完全粗糙(α=1)时两者误差约14%～20%。鉴于Ito理论模型是基于金属挤压与碾压过程模拟而得出的，其计算的被动荷载随桩间距的降低急剧增大，因此在桩间距较小时的计算结果并不理想[7]。本文计算结果在桩间距相对较小(≤2d,D2/D1≤0.5)时，明显低于Ito模型；而当桩间距大于2d(D2/D1>0.5)时，与Ito模型较为一致，相对更为合理。

同时，结合工程实例进一步验证桩周位移土塑性区不同开展范围时桩身被动荷载简化计算方法。张家港XZ高速某枢纽[17]工程场区浅部分布有一层流塑状的淤泥质粉质黏土(厚约8.9 m)和一层流塑状的低液限粉质黏土(厚约4.1 m)，在下穿匝道路基堆载作用下，匝道坡址处主线高架桥墩柱发生偏移。基于本文桩身被动荷载简化确定方法，对坡址处左幅31#墩和32#墩基桩-立柱内力变形进行计算分析，如图9所示。

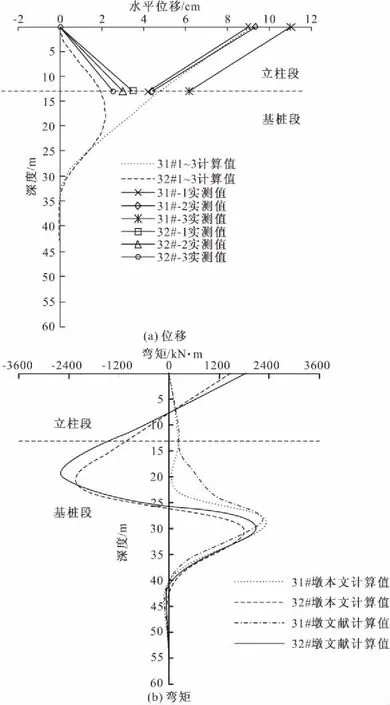
图9 基桩-立柱受力响应计算结果

计算中，场区各土层物理力学指标详见文献[17]，其中淤泥质粉质黏土内摩擦角为3.7°，计算时可近似取0°，该软弱层符合Tresca屈服准则假定。下穿匝道路基高5.15 m，顶宽8.5 m，底宽32.5 m；临近桥墩基桩长46 m，桩径1.5 m；墩柱长13 m，直径1.2 m，柱顶轴力5090 kN；桩、柱混凝土材料重度γG=25 kN/m3，弹性模量Ep=28.5 GPa；考虑桥墩支座形式不同，31#柱顶为滑动支座，柱顶边界取弯矩Mc0=0 kN·m，剪力Vc0=0 kN，32#柱顶为固接，柱顶边界取位移yc0=0，转角φc0=0。考虑位移土与基桩的相互作用，桩土摩擦系数近似取α=0.5，据此采用本文计算模型回归确定计算参数：λ=2.2，a=2.0，b=1.4。

可以看出，采用本文桩身被动荷载确定方法计算所得立柱偏移量与实测结果较为接近；桩柱弯矩与文献[17]采用Ito修正模型计算的桩柱弯矩变化规律一致，能够很好地反映31#和32#墩实际变形特征与受弯开裂特点。

4 结 论

本文主要针对桩周位移软土作用于被动桩的荷载效应开展研究，结论如下：

(1)基于滑移线理论，构建了桩周位移软土与基桩的相互作用计算模型，并根据位移土塑性区开展范围，推导建立了考虑位移土塑性区局部开展影响的桩身被动荷载计算公式；

(2)根据桩周位移土不同塑性区时桩身被动荷载与桩前法向应力水平的分析，建立了边载工况下基于桩前法向应力的桩身被动荷载简化计算方法；

(3)通过与工程案例实测、文献方法计算结果的对比，验证了本文计算模型的可行性，简化计算方法公式简洁，且概念明确，较易为工程人员掌握应用，可为类似被动桩设计验算提供参考。