连续刚构桥顶板束的配束设计方法研究

2020-07-21赵小龙李新平耿蒙蒙

四川建筑 2020年1期

赵小龙，李新平，耿蒙蒙

(1.华南理工大学土木与交通学院，广东广州 510641； 2.碧桂园控股有限公司，广东广州 511300)

大跨度连续刚构桥一般采用悬臂施工的施工方法，具有行车平顺、方便施工、受力明确等优点，因此受到广大工程师的喜爱。尤其是在跨线、跨河时，采用连续刚构桥已成为桥梁工程师的不二之选。但是，随着服役时间的增长，大部分大跨度连续刚构桥出现了跨中挠度过大的现象，进而导致箱梁梁体开裂，而箱梁的开裂反过来又会进一步加大下挠，如此反复循环[1-2]。由于这个原因，使得预应力混凝土连续刚构桥朝更大的跨径发展受到制约。因此，本文从减小跨中下挠出发，研究大跨度连续刚构桥的配束设计方法，以恒载零弯矩法为依托提出了顶板束的三组配束设计方法，旨在减小成桥时的跨中下挠。

1 顶板束配束理论

范立础院士在《预应力混凝土连续梁》一书中提到：连续箱梁桥悬臂施工时可以利用钢束预应力来平衡施工时梁体节段的自重，这样就使得箱梁只受到轴向压力的作用，于是箱梁只有轴向变形而无弯曲变形，这就是“恒载零弯矩法”的基本理论。而连续刚构桥在采用悬臂施工时，顶板预应力束的张拉就是为了平衡施工时的梁体自重。如果箱梁在形成最大T构时，所有顶板预应力束能正好平衡结构自重，那么在成桥后，收缩、徐变次内力就会很小，于是桥梁的长期挠度也相应较小。

然而在实际施工过程中，不可能达到以上所述的平衡状态[3]，但可以通过张拉预应力顶板束来平衡结构自重在某些危险截面上的内力。对于悬臂施工的连续刚构桥，在施工过程中最危险截面为悬臂根部截面，因此，一般应使在某节段张拉的顶板预应力束在悬臂梁根部产生的正弯矩平衡掉该节段自重在悬臂梁根部产生的负弯矩，具体分析如下。

大跨度预应力混凝土连续刚构桥多采用变截面箱梁，因此每个节段的重量是不一样的，具体受力分析以及相应的弯矩见图1。

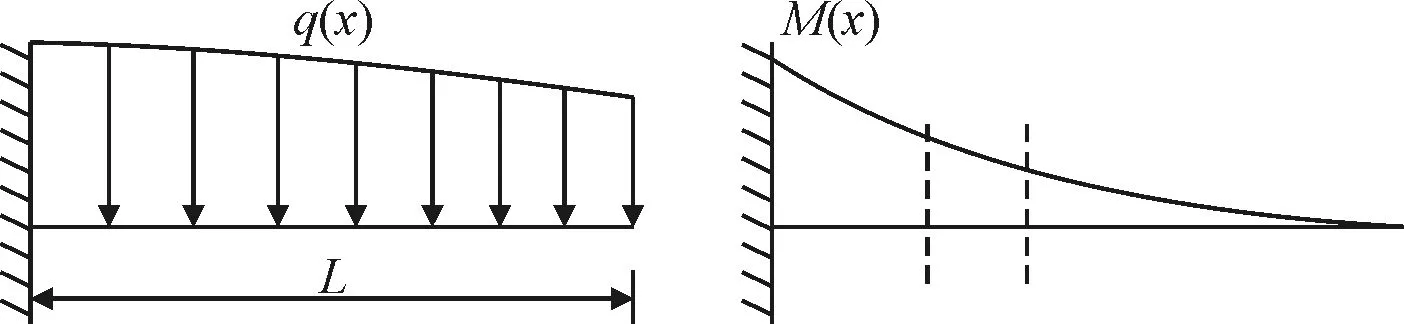
图1 悬臂箱梁受力分析

箱梁梁高方程一般为二次抛物线，设梁高方程为h(x)=ax2+bx+c，则悬臂箱梁正视图如图2所示。

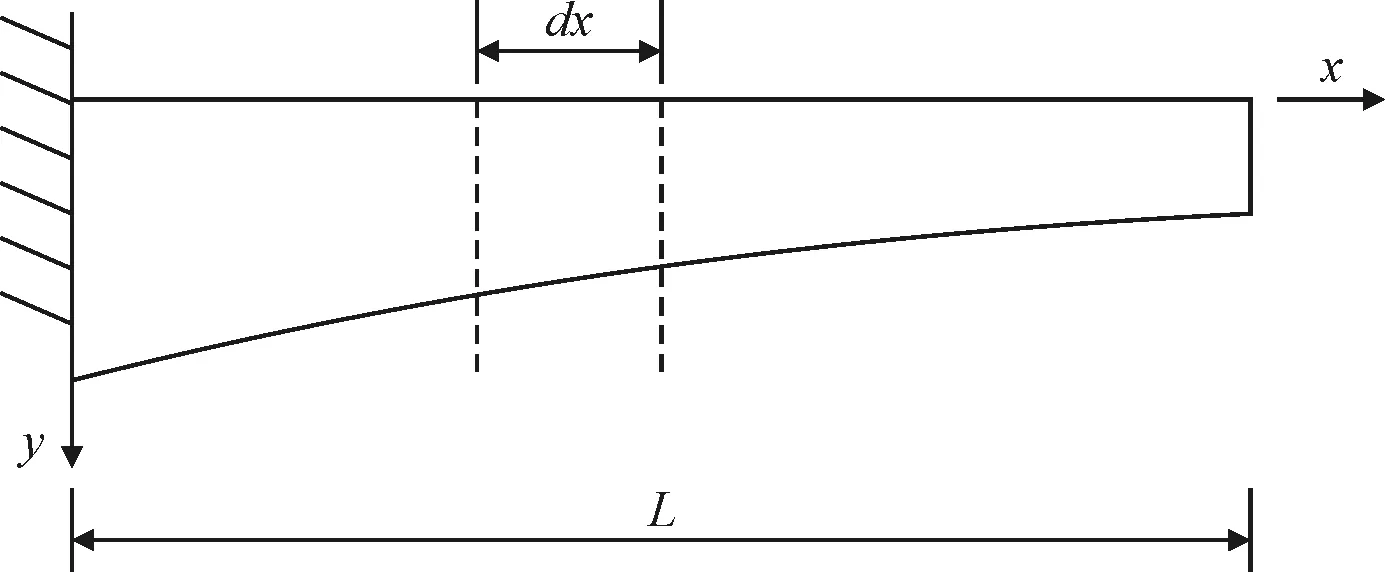
图2 悬臂箱梁正视图

每个节段的梁高是变化的，可以得到悬浇的ij段混凝土重力为：

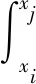
(1)

进一步对悬臂梁根部取矩，可以得到ij节段自重在根部产生的负弯矩：

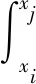
(2)

式中：A(x)为截面面积；γ为混凝土容重；xi、xj为悬浇段i、j截面距离悬臂梁根部的距离。

ij节段张拉的顶板束在悬臂梁根部产生的正弯矩为：

Mpj=Npj(yu-ap)

(3)

根据恒载零弯矩法，对悬浇的ij段进行配束，则有：

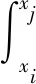
(4)

式中：yu为截面形心到上缘的距离；ap为预应力束的保护层厚度。

则由式(4)可以得到ij段的预应力Npj为：

(5)

考虑到预应力的损失，按张拉控制应力的85 %进行计算，可得：

(6)

式中：σcon为钢绞线的张拉控制应力，常取1 395MPa；A为单根钢绞线的面积，对于常用的φs15.2钢绞线取139mm2；np为ij段需配置的顶板束总根数。

根据以上的配束方法能够得到每个悬浇段所需配置的顶板束根数，但按此方法得到的每个悬浇段的顶板束根数是不相同的，考虑到施工的便利，一般把所有的悬浇节段分为若干组，让每个组内每个悬浇节段张拉的预应力钢束数量相同，所以还应调整每个节段的预应力钢束数量，从而使得每个节段张拉的预应力束数相同。

基于以上说明，本文提出顶板束的“三组配束”设计方法，即：将所有浇筑节段分成三组，从1号块到最大悬臂端分别为第一组、第二组、第三组。文献[4]以恒载零弯矩法为依托，论证出连续刚构桥的顶板束采用“大悬臂大配束”的配索方案，能显著减小桥梁在成桥后的跨中下挠。经过本文作者的不断试算，最后提出采用全桥总钢束数量的平均值作为第二组顶板束的配置，采用第三组内各个节段的钢束取平均值作为第三组顶板束的配置，然后利用全桥总钢束量得到第一组的顶板束配置量。

但是应当怎样划分为三组才能达到最好的成桥状态，本文提出了四种分组方案：

方案一：采用均等划分，让每个组内的节段数相等。

方案二：第一组包含的节段数最多，第三组包含的节段数最少，第二组居中。

方案三：第二组所含节段数最多。

方案四：第一组包含的节段数最少，第三组包含的节段数最多，第二组居中。

下节将以实桥工程为依托建立Midas有限元模型，对这四种方案进行比较分析，得出最好的划分方案。

2 顶板配束方案对比分析

某主跨为150m的预应力混凝土连续刚构桥，桥宽为21.5m，箱梁梁高采用二次抛物线变化，箱梁采用单箱双室截面，主墩采用双薄壁墩，桩基采用钻孔灌注桩。钢束采用Φs15.2的高强度低松弛的预应力钢绞线，抗拉强度标准值为为1 860MPa。

主桥上部结构采用悬臂施工，箱梁纵向一共有21种节段，分别为18个现浇段、零号块、合拢段和边跨现浇段。其中18个现浇段和合拢段采用悬臂现浇施工，边跨现浇段采用满堂支架施工。单个T构最大悬臂长为74m，Midas有限元模型如图3所示。

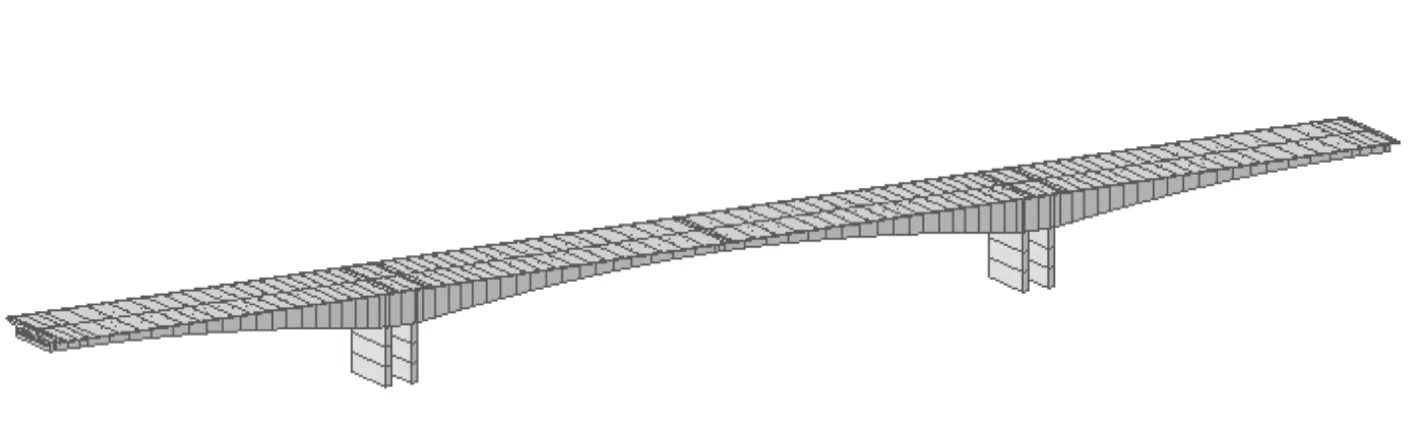
图3 有限元模型消隐

根据所建立的Midas有限元模型，查询得到悬臂施工过程中每个号块的重量以及每个号块自重对悬臂梁根部产生的负弯矩。根据结构的对称性，本文仅一个T构进行配束计算，各个悬浇段的自重以及各节段自重对悬臂梁根部的负弯矩统计如表1所示。

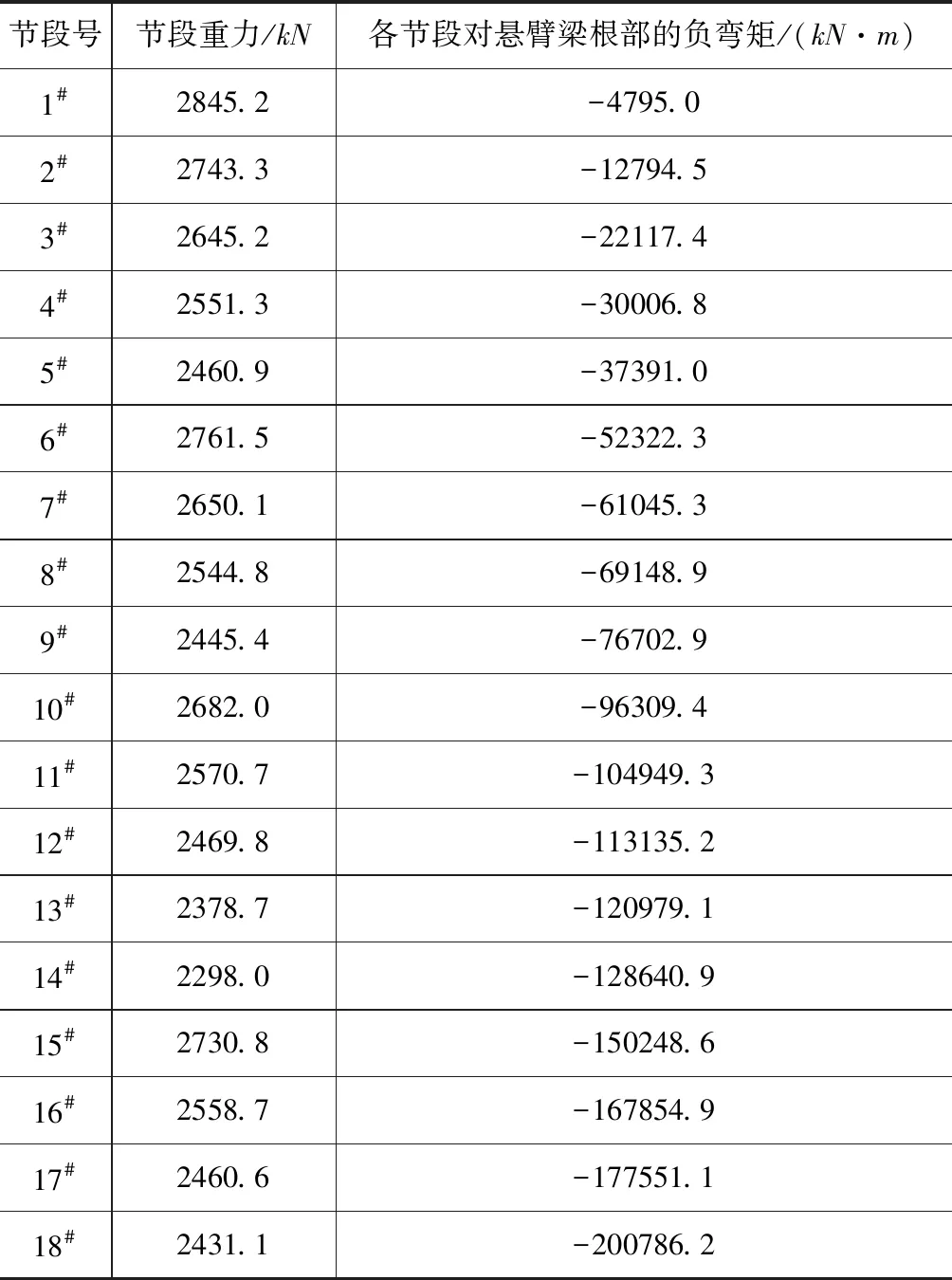
表1 各节段重力以及悬臂梁根部弯矩统计

悬臂梁根部的梁高为8.5m，其截面形心到上缘的距离是4.14m，顶板束布置为两层，其钢束形心至顶板上缘的距离分别为0.15m和0.31m，由表1以及式(5)可得到为平衡各个节段重量产生的根部截面负弯矩所要施加的有效预应力，再由式(6)可得每个节段所需配置的顶板束根数。计算结果详见表2所示。

由表2可知，每个悬浇节段需要张拉的的顶板束根数是不相同的，为使施工方便，采用本文提出的“三组配束”对顶板束数量进行调整。根据上节提出的划分方法，分别调整各组的顶板束数量。

方案一：采用均等划分，即：第一组为1#～6#块，第二组为7#～12#块，第三组为13#～18#块，按前文所述的钢束配置方法得到各组中每个节段张拉的顶板束数量为：第一组每节段张拉87根，选用4φs15.2～22；第二组每节段张拉139根，选用6φs15.2～23；第三组每节段张拉192根，选用8φs15.2～24。将配束结果代入到Midas/Civil中得到成桥状态下的位移曲线，如图4。

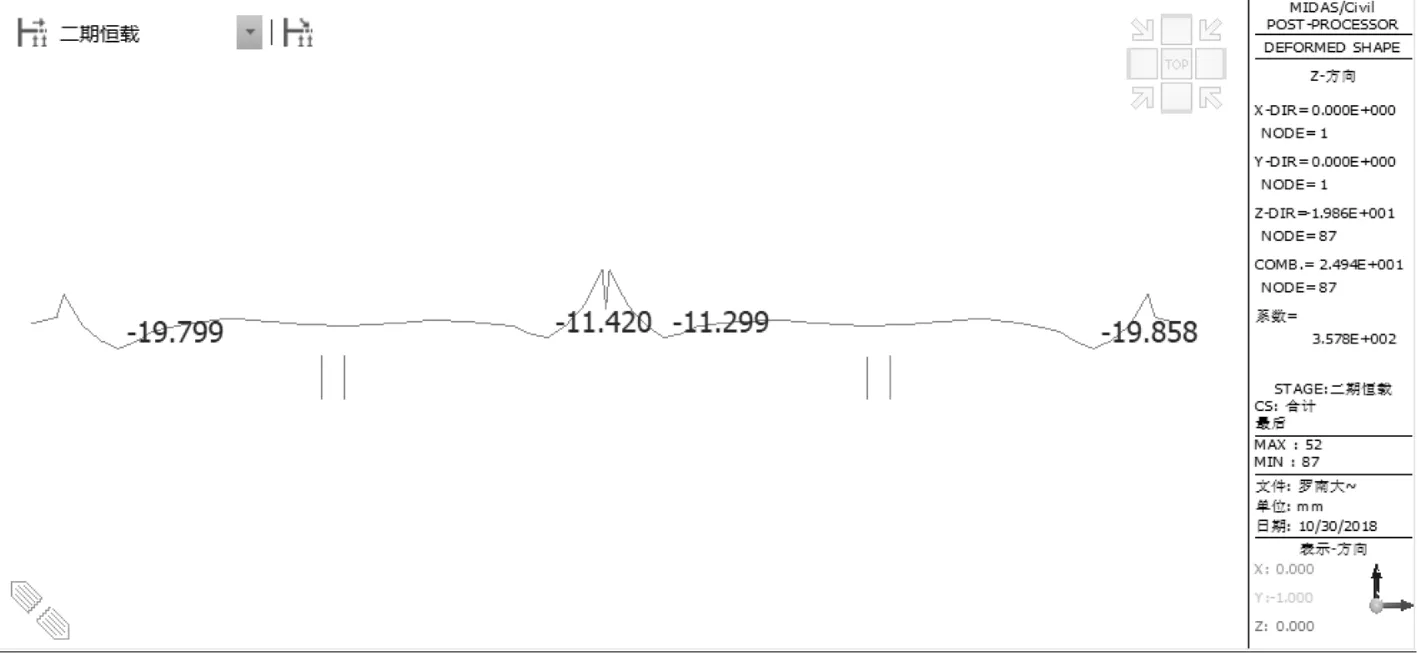
图4 方案一对应的成桥位移

方案二：第一组包含的节段数最多，第三组包含的节段数最少，第二组居中。即：1#～8#块为第一组，9#～14#块为第二组，15#～18#块为第三组，各组中每个节段张拉的顶板束数量为：第一组张拉115根，选用6φs15.2～19；第二组张拉139根，选用6φs15.2～23；第三组张拉190根，选用8φs15.2～24。

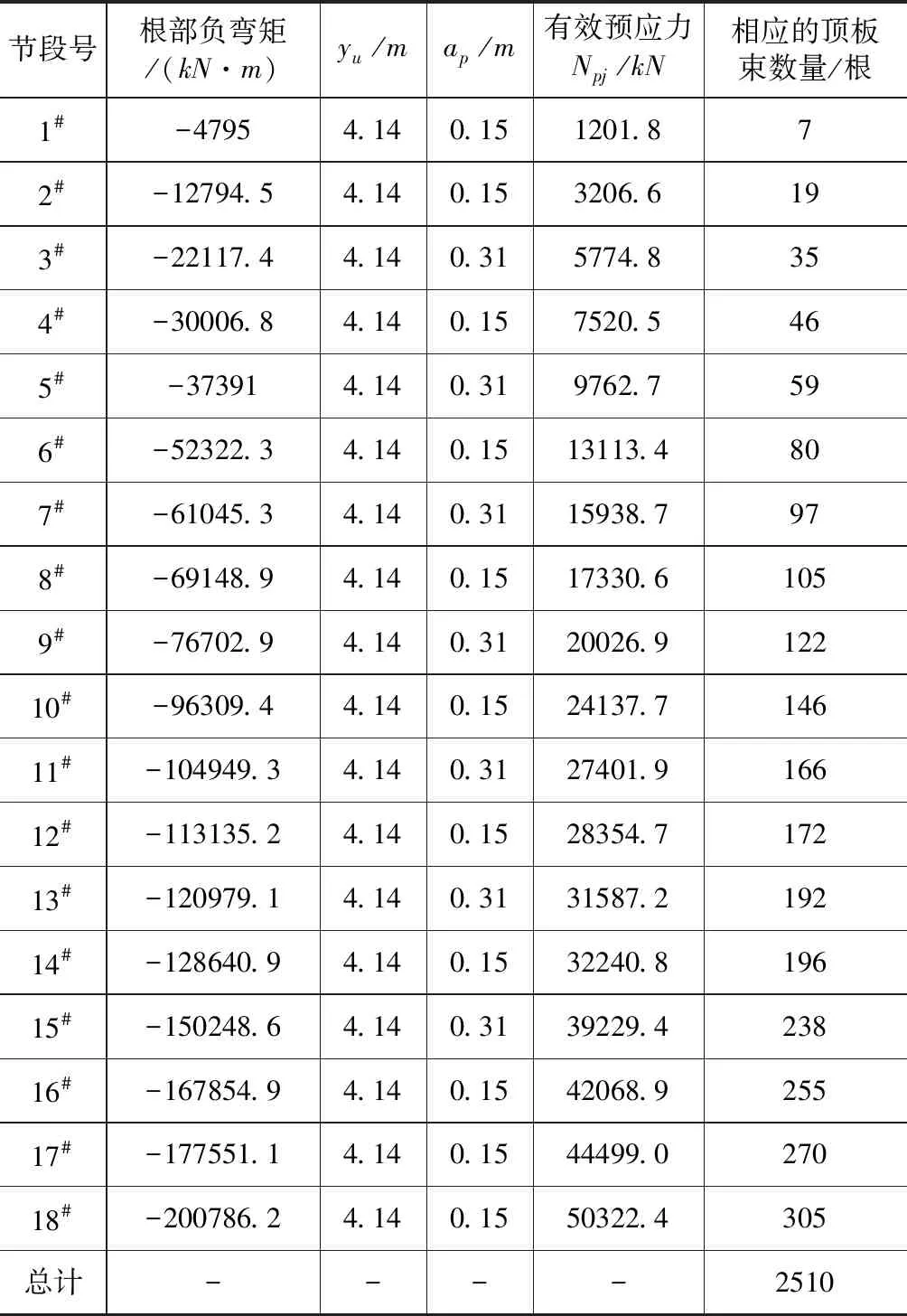
表2 各节段所需的有效预应力及相应的顶板束数量

成桥位移曲线如图5。

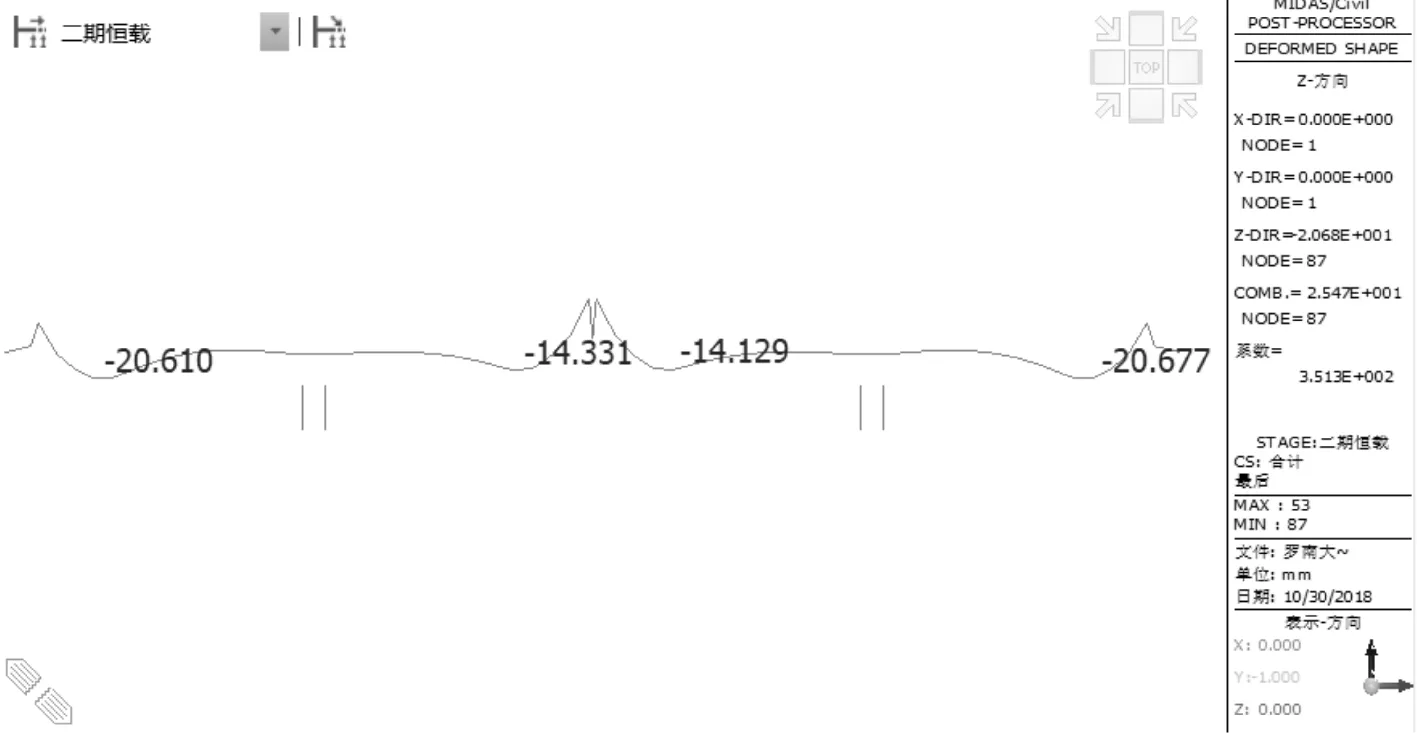
图5 方案二对应的成桥位移

方案三：第二组所含节段数最多，即：1#～5#块为第一组，6#～13#块为第二组，14#～18#块为第三组，各组中每个节段张拉的顶板束数量为：第一组张拉88根，选用4φs15.2～22；第二组张拉139根，选用6φs15.2～23；第三组张拉192根，选用8φs15.2～24。成桥位移曲线如图6。

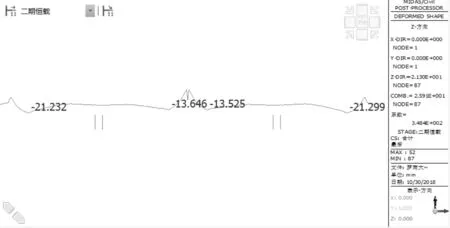
图6 方案三对应的成桥位移

方案四：第一组包含的节段数最少，第三组包含的节段数最多，第二组居中。即：1#～4#块为第一组，5#～10#块为第二组，11#～18#块为第三组，各组中每个节段张拉的顶板束数量为：第一组张拉47根，选用2φs15.2～24；第二组张拉139根，选用6φs15.2～23；第三组张拉186根，选用8φs15.2～23。成桥位移曲线如图7。

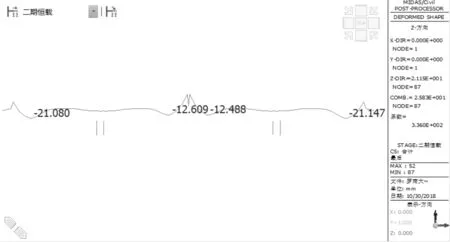
图7 方案四对应的成桥位移

原设计成桥位移曲线如图8所示。

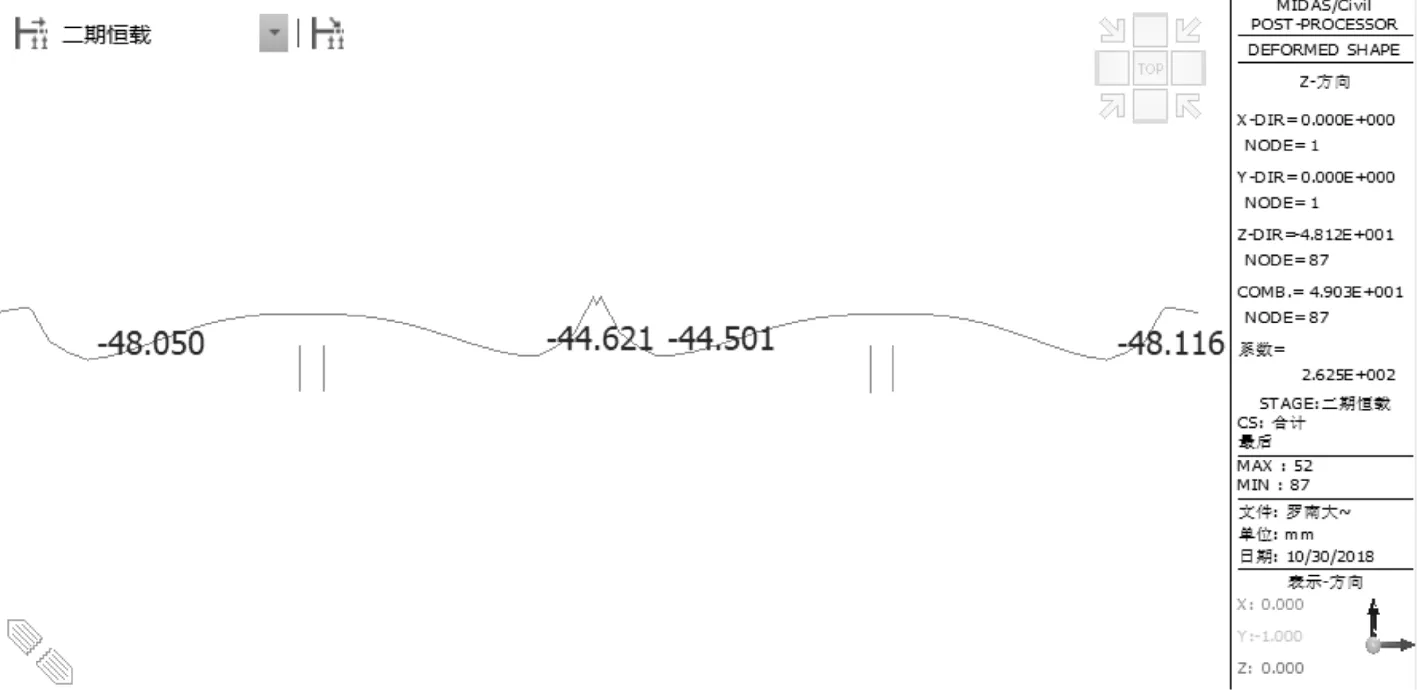
图8 原设计成桥位移

四种分组方案及原设计方案在成桥状态下最大下挠汇总如表3,钢束统计数量见表4。由表3、4可知，本文提出的配束方法(方案一～四)与原设计方案相比增加了15%的钢束用量，从经济方面考虑，原设计方案更优。究其原因主要为：(1)本文是从弯矩平衡角度出发配置预应力钢束，实际就需要平衡这么多的弯矩，钢束增加不可避免。