基于小波包分析与支持向量机的斜拉索损伤识别
2020-07-21
(石家庄铁道大学 工程力学系,河北 石家庄 050043)
近年来,斜拉桥因其跨越能力强、结构形式简洁美观、良好的力学性能和经济指标等优点,得到广泛的应用。斜拉索作为斜拉桥的主要受力构件,它的损伤会对桥梁结构的安全性、整体性和静动力特性等产生不利影响,对于桥梁的安全运营及养护具有极其重要的价值,对事故的预防和生命财产安全具有重大的意义。因此,斜拉索的损伤问题引起了许多学者的高度重视,并进行了深入的研究[1-4]。
小波包分析可以放大结构的振动响应,被越来越多地应用于损伤识别领域。丁幼亮等[5]在对振动响应小波包分析的基础上,利用小波包脉冲响应函数及小波包能量谱识别结构损伤。Law et al[6]利用灵敏度方法对一框架结构进行了参数识别。朱劲松等[7]提出了一种小波包能量变换率平分和损伤识别指标,通过简支梁模型的数值仿真,验证了该指标损伤识别的可行性。何浩祥等[8]提出基于小波包脊的时变频率提取办法,并对结构多维地震损伤进行了识别。刘习军等[9]利用小波包分析计算结构能量最大的单阶模态响应指标,并利用该指标对简支梁损伤识别进行了数值模拟。近年来基于小波分析与人工神经网络相结合的结构损伤识别方法得到了迅速发展,Hou et al[10]提出了一种利用小波变换和神经网络进行调制信号的识别方法。管德清等[11]将小波分析与神经网络结合进行框架损伤位置和程度的识别。肖书敏等[12]利用小波神经网络方法对桥梁结构损伤进行了定位。综上所述,基于小波包分析和支持向量机相结合的损伤识别方法在工程领域的应用尚不多见,而应用于斜拉索损伤识别研究目前还尚未有相关文献报道。
鉴于小波包分析具有较高的分辨率以及支持向量机优良的泛化能力,本文提出一种小波包分析与支持向量机相结合的损伤识别方法,并将其应用于斜拉索损伤识别领域,利用小波包理论对索梁锚固点的加速度时程响应进行小波包分解,构造小波包能量变化率指标,在此基础上,进行支持向量机损伤识别模型的构建,对斜拉桥拉索损伤识别进行研究。
1 损伤识别指标
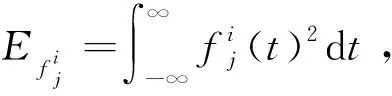
(1)
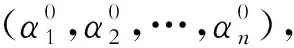
(2)
(3)
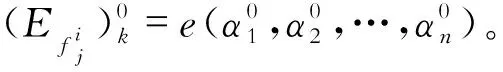
整理之后写成增量的形式为
(4)

由式(4)可以看出:各组分能量变化量是以损伤因子为自变量的函数值,分能量变化量与损伤存在内在联系,因此可以以各组分能量变化量为基础构造损伤指标。
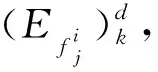
(5)
2 支持向量机基本原理
2.1 分类原理
设样本集为
(xi,yi),i=1,2,…,n,xi∈Rn,yi∈(1,36)
(6)
式中,xi为第i个位置损伤时的小波包能量变化率向量;yi为xi对应的期望输出。
支持向量机的主要思想是找出最优分类超平面,所谓最优分类,就是要求不但能正确分开,而且使分类间隔最大,分类间隔等于2/‖ω‖,使分类间隔最大等价于使1/2‖ω‖2最小,满足此条件的就是最优分类线,推广到高维空间,分类线就是分类面。分类超平面的标准形式会受到约束条件的限制,在约束条件下,通过求解优化问题最终可以得到最优分类函数
(7)
2.2 回归原理
损伤程度识别就是利用支持向量机进行回归分析,其核心思想就是通过训练样本得到回归估计函数,然后利用回归估计函数进行损伤程度的预测。假设所有样本集都在精度ε下无误差地进行线性函数拟合,寻找最小的ω可以表示为最优化问题
(8)
约束条件
(9)
通过在约束条件下求解最优化问题即可得到回归估计函数。如果存在ε精度下不能估计的数据,通过引入松弛变量、拉格朗日函数和对偶变量,再根据最优解条件(KKT条件)求得参数,最终得到回归估计函数
(10)
3 基于小波包分析与支持向量机的斜拉索损伤识别

图1 斜拉索损伤识别流程
通过 车桥耦合振动分析得到斜拉索损伤前后索梁锚固点的加速度时程响应,对其进行小波包分解得到能量变化率指标,建立面向斜拉索损伤识别的支持向量机损伤识别模型,以小波包能量变化率损伤指标作为支持向量机的输入参数,斜拉索的损伤因子作为支持向量机的输出表示斜拉索损伤程度,损伤识别流程如图1所示。
4 数值验证
4.1 有限元模型
以缩尺为50的实验室独塔斜拉桥模型桥为研究对象,实验模型的构造见文献[13]。采用大型通用有限元分析软件ANSYS建立该模型桥的有限元模型如图2所示,主梁和桥塔采用SHELL63壳单元模拟,斜拉索采用LINK10单元模拟,全桥共10 312个节点,7 619个单元。斜拉索的编号如图3所示,将每根斜拉索看成一个区域,共有36个区域。
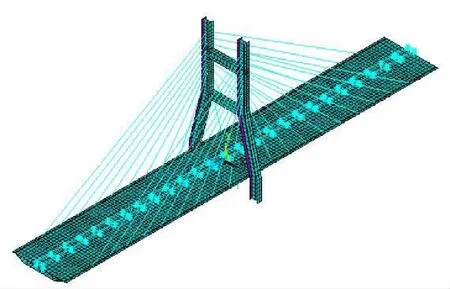
图2 斜拉桥有限元模型

图3 斜拉索区域编号布置图
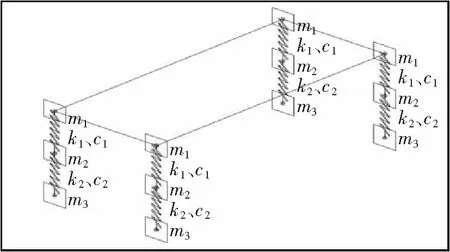
图4 车辆模型图
建立汽车的全车模型,如图4所示。将车体简化为4个只有竖向自由度的质量块,用m1表示,相互之间通过刚臂进行连接;悬架和轮胎简化为弹簧阻尼系统,其质量分别简化为只有竖向自由度的质量块,用m2、m3表示;分别用k1、c1表示车体与悬架之间弹簧阻尼系统中的弹簧刚度和阻尼系数;k2、c2表示悬架与车轮之间弹簧阻尼系统中的弹簧刚度和阻尼系数。该模型能综合考虑车的竖向、俯仰及侧仰自由度,与真实汽车受力情况相似。根据相似理论,按照1∶50的缩尺比对汽车缩尺,车辆具体参数如表1所示。

表1 车辆参数表
4.2 斜拉索小波包能量变化率指标
以4#斜拉索损伤前后为例,给出索梁锚固点的加速度时程响应曲线,如图5所示,5种损伤程度的能量变化率指标如图6所示。
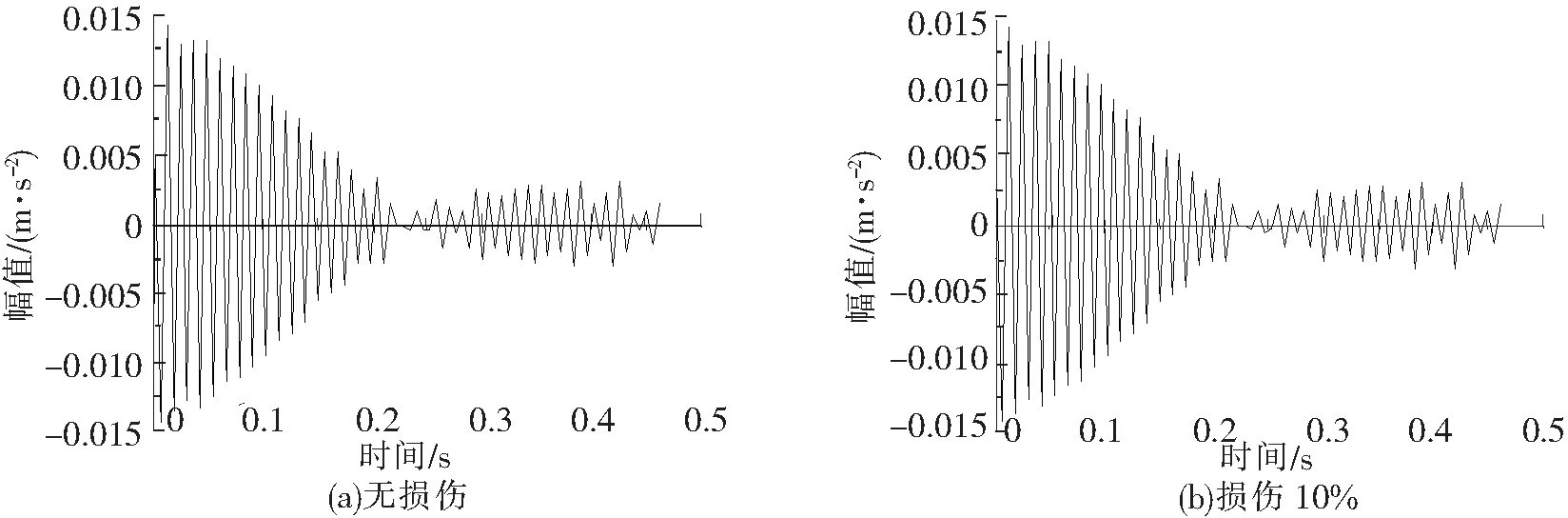
图5 4#斜拉索损伤前后锚固点时程响应曲线

图6 4#索索梁锚固点小波包能量变化率指标
对比图4、图5,很难识别出斜拉索的损伤位置及损伤程度。由图6可知,斜拉索发生不同损伤程度时索梁锚固点的能量变化率逐渐增加,且大致呈线性关系,据此可以进行斜拉索损伤程度的识别。
4.3 斜拉索损伤识别
将36根斜拉索分别按5种损伤程度(5%、10%、15%、20%、25%)进行损伤模拟,共180种损伤工况。分别提取在各个工况下索梁锚固点的加速度时程响应,并进行小波包分解,进而构造得到小波包能量变化率损伤指标,再利用支持向量机进行损伤识别。其中以损伤程度15%、20%和25%时36个斜拉索损伤样本作为测试集,其余斜拉索损伤样本作为训练集进行训练。损伤程度的预测结果及误差如表2所示。
由表2可知,当预测损伤程度为15%时,所有位置的损伤程度预测误差均在5%范围内,平均损伤预测误差仅为1.5%;当预测损伤程度为20%时,所有位置的损伤程度预测误差均在5%范围内,平均损伤预测误差仅为0.9%;当预测损伤程度为25%时,平均损伤预测误差仅为0.8%。说明本方法对斜拉索损伤程度的预测精度较高,且随着损伤程度的增加,平均预测误差逐渐减小。
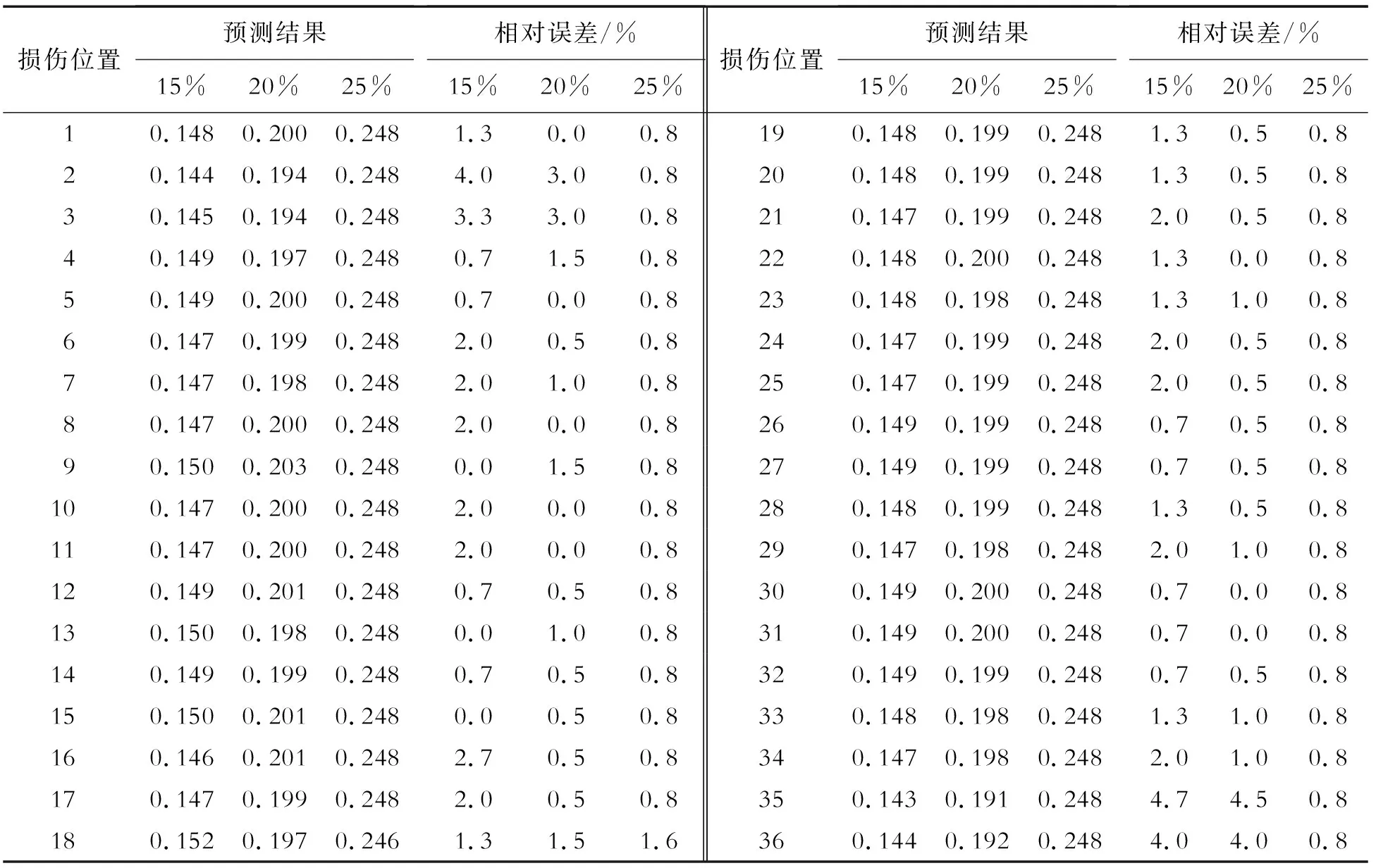
表2 损伤程度预测结果及误差
4.3.1 输入向量个数对识别结果的影响
以损伤程度15%为例,分别考虑输入向量的个数为4、12和20 3种情况,采用交叉验证法进行SVM参数优化,识别结果如图7~图9所示。
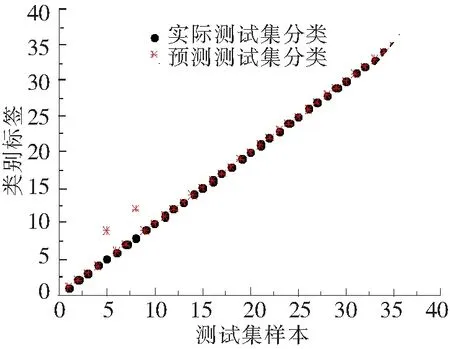
图7 4个输入向量时识别结果
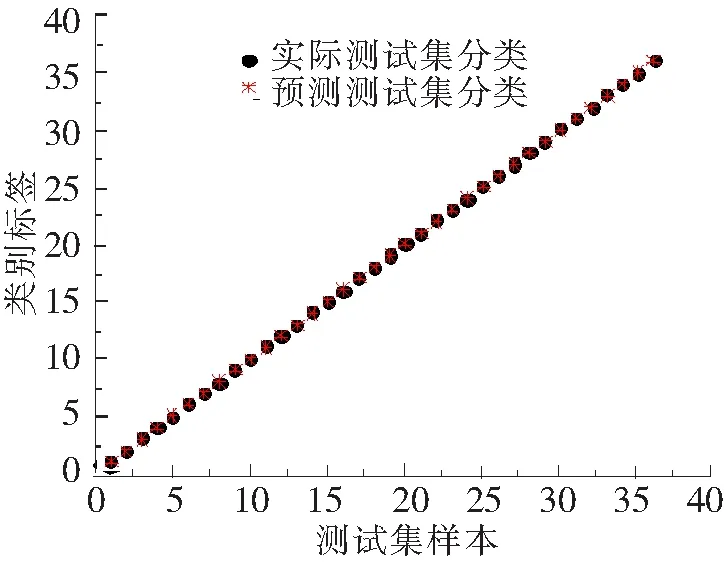
图8 12个输入向量时识别结果
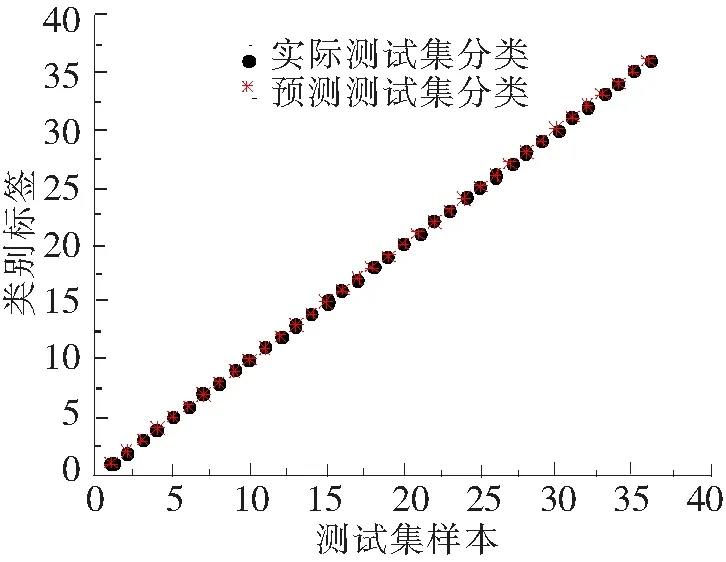
图9 20个输入向量时识别结果
由图7~图9可知,当输入向量个数为4时,识别正确率均为94.44%;当输入向量个数为12时,识别正确率已经达到了100%,输入向量个数为20时同样是100%。这表明该方法对输入向量个数要求不高,少量的输入向量即可达到较高的识别正确率。
4.3.2 噪声影响分析
由于实际工程中,测试信号不可避免地会受到噪声干扰。为了研究噪声对本方法识别结果的影响,通过对模拟得到的加速度时程响应加入不同程度噪声来模拟现场测试时被噪声污染过的实际加速度时程响应。即
Fm=Fc+Eρrand(N)×σ(Fc)
(11)
式中,Fc为模拟得到的加速度时程响应;Fm为噪声影响后的加速度时程响应;Eρ为噪声等级,用百分数表示;rand(N)为零均值、单位标准差满足标准正态分布,且与原始数据等长(长度为N)的随机数列向量;σ(Fc)为加速度时程响应的标准差。
主要讨论了噪声等级为1%、2%、5%的3种情况,损伤程度预测结果如图10所示。

图10 损伤程度识别误差
由图10可知,本方法在噪声污染情况下仍可以进行斜拉索的损伤识别,且保持有较高的识别率,说明本方法对噪声污染具有一定的鲁棒性。但同时可以看到:随着噪音等级的增加,位置识别正确率逐渐降低,损伤程度平均预测误差逐渐增大。
5 结论
基于小波包分析与支持向量机相结合的损伤识别方法,理论上可以实现对斜拉索损伤程度的较高精度预测;随着损伤程度的增加,平均预测误差逐渐减小,且只需少数输入向量即可得到较高的斜拉索损伤识别正确率。该方法对噪声污染具有一定的鲁棒性,但随着噪声水平的增大,平均预测误差呈增加趋势。本方法的实用性尚需试验验证。
