不均衡闸瓦压力下重载机车曲线通过动态行为
2020-07-21
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
0 引言
随着国民经济水平的提升,重载货运因其具有投资少、效益高、安全性好等特点[1],备受国内外铁路运输行业的关注。伴随着载货运能的提升,对重载列车的服役性能要求也越来越高,国内外众多学者进行了大量相关研究,旨在提高列车的运行安全性及解决实际运营当中暴露出的故障问题,其中制动故障近年来频频在各机务段等相关运营单位检修维护中记录报备,如徐州北机务段配备28台DF8B机车,其中就有5台机车发生单元制动器不制动故障[2];另外,踏面制动器由于结构问题存在卡滞及缓解不良的状态,因而导致与闸瓦托相连的悬挂连杆断裂甚至失效,从而导致制动故障发生[3-4]。同时在相关的运行安全性及列车动力学研究层面,马卫华等[5]研究了中间轴自由横动量对2C0机车曲线通过动力学性能的影响,分析了机车曲线通过性能及横向平稳性的动态行为;朱剑林等[6]建立六轴重载机车模型,分析了车辆曲线通过安全性,并研究了一、二系悬挂参数对车辆曲线通过动力学性能的影响;陈辉辉等[7]对大秦线上运行的2万t重载组合列车进行了研究,分析了制动条件下空车及重车下的曲线通过动力学性能;林丽等[8]研究改进三轴转向架曲线通过性能,采取降低中间轴一系悬挂横向刚度方案,分析了车辆过曲线时的动力学特性及规律;魏静等[9]建立车辆-轨道耦合非线性系统动力学仿真模型,分析了不同轮径差下,车辆通过曲线时的动力学性能;刘朝辉等[10]分析研究了六轴重载机车在压钩力作用下重载机车曲线通过安全性,对车钩动态响应及机车运行安全性进行了相应评估;Simson et al[11]研究了三轴转向架的曲线通过性能,提出了一种新型转向架设计方案,此种转向架具有良好的曲线通过性能;Liu et al[12-13]建立重载列车-轨道三维耦合动力学模型,研究在纵向冲动下,重载机车过曲线时车钩力动态响应特性。
综合以上,众多学者研究分析重载机车曲线通过安全性,大多在均衡制动状态下分析研究,而在实际中存在不均衡制动状态,即同一轮对左、右侧闸瓦压力及制动力不一致,并且关于不均衡制动状态下机车的动态行为研究比较少。另外,在制动过程中,制动力主要对车辆纵向动态响应较为明显,闸瓦压力直接作用于轮对,对轮对的摇头、横移运动产生影响。为了突出闸瓦压力对轮对的作用效果,更有效地反映在闸瓦压力作用下轮对动态响应变化规律,在研究过程中并未考虑制动力的作用,仅从单纯的闸瓦压力作用入手分析,研究在单纯不均衡闸瓦压力作用下重载机车曲线通过性能,揭示不均衡闸瓦压力的影响规律。
1 重载机车模型建立及仿真设置
1.1 重载机车模型
以我国重载铁路中运营的HXD型六轴重载机车为研究对象,如图1所示,在多体动力学仿真软件UM中建立分析模型。图2给出了模型结构拓扑关系,由图可知模型总计84个自由度,分别考虑轴箱、电机及其吊杆的点头运动,牵引杆考虑3个自由度(伸缩、横摆、沉浮),车体、构架、轮对等机车主要结构组成考虑6个自由度,同时将轨道模型简化为无质量轻型钢轨,并且考虑了一、二系减振器,中间轮对自由横动量等关键非线性力学关系。

图1 UM中建立的机车动力学模型
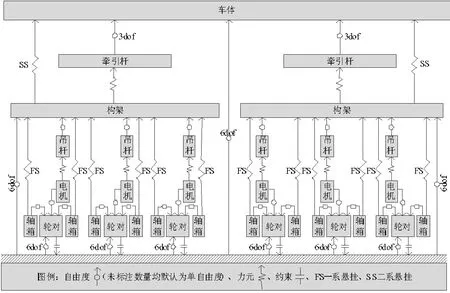
图2 模型拓扑关系
1.2 模型验证
根据文献[14]中计算条件及实测数据,验证模型的准确性。试验及仿真条件:轨道激励以我国干线轨道不平顺作为激扰,惰行工况,运行速度70 km/h, 60 kg/m钢轨,轨底坡1/40 m;线路条件:直线100 m、缓和曲线70 m、曲线半径300 m、曲线长160 m、超高120 mm。图3给出了一、六位轮对轮轨垂向力及轮轨横向力通过曲线时,动态响应对比验证,根据图3(a)和图3(b)一位及六位轮轨垂向力,在线路过渡处(直缓点、缓圆点、圆缓点、缓直点)取到峰值,进入圆曲线段后趋于稳定平稳变化,由于线路实测数据轨道不平顺更为复杂,且与仿真中施加的轨道激励存在一定差异,故对比结果存在一定的误差,过曲线时一位内外轮实测结果分别在90 kN、145 kN附近波动,仿真结果在90 kN、150 kN上下波动,六位内外轮实测结果在110 kN、130 kN附近波动,仿真结果在85 kN、145 kN上下波动,模型计算轮轨垂向力结果较为准确;由图3(c)、图3(d)可知,轮轨横向力动态响应变化规律同轮轨垂向力相仿,同样在线路过渡处产生突变取到峰值,仿真计算与实测数据也存在一定差异,但整体计算结果与实测数据较为接近,误差在可接受范围内,从轮轨横向力及垂向力的对比验证可知,模型计算结果较为准确,可以展开仿真分析。
2 闸瓦压力确定及仿真方案
2.1 闸瓦压力计算
机车制动的过程较为繁琐,在制动过程中为了简化计算便于模型仿真,参考文献[15]中实算闸瓦压力,单个闸瓦压力为
(1)
式中,各参量的意义及取值在表1中给出,部分数值参考文献[16]和文献[17],经计算每个制动单元踏面所受闸瓦压力为F=51.92 kN。
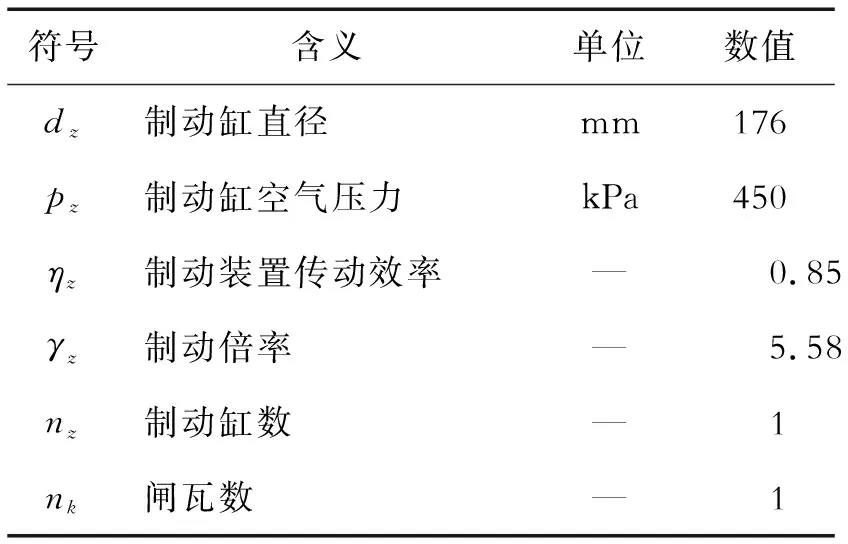
表1 实算闸瓦压力参数
2.2 模拟仿真方案
图4给出了仿真方案,重载机车单元制动器布置如图4(a)所示,两侧闸瓦制动器对称布置,仿真方案选取各轮对左轮发生制动故障,只有右轮制动,并选取机车紧急制动时的运行状态,此时闸瓦压力将达到最大,表2为计算工况,图4(b)为仿真计算方案,其中工况4是正常工况,即机车惰行状态下正常通过曲线,图4(b)中,FiLx和FiRx(i=1~3)分别为施加在左、右侧车轮上的闸瓦压力,前后转向架对称布置,故只在前转向架一、二、三位轮对上分别施加闸瓦压力分析计算即可。

表2 计算工况 kN

图4 仿真分析方案
仿真线路条件:直线段100 m,缓和曲线段100 m,圆曲线段200 m,曲线半径400 m,超高120 mm,轨底坡1/40;JM3标准踏面,钢轨60 kg/m,速度70 km/h;同时为了便于仿真计算及更有效地反映在单纯闸瓦压力作用下机车动态行为,仿真中并未施加轨道激励。
3 动力学性能分析
为研究通过曲线时机车动态响应特性,首先分析各工况下轮对横移量、摇头角,初步确定运动状态最为剧烈的工况及轮对,随后进一步分析轮轨横向力、轮轨垂向力、脱轨系数、磨耗功率等指标,从而最终确定过曲线时机车最严重工况,同时反映不均衡闸瓦压力作用下重载机车通过曲线时轮轨动态行为变化规律。
3.1 轮对运动状态分析
对不同工况条件下轮对横移及摇头角进行对比分析,以工况1条件下时程响应为例,分析轮对通过曲线时响应规律,同时给出不同工况下轮对横移、摇头角幅值统计,以此对比分析不同工况下轮对运动状态剧烈程度。图5给出了工况1条件下轮对横移时程响应及各工况下轮对横移幅值对比分析,由图5(a)可知,轮对横移动态响应均在缓和曲线处突变,整体看所有轮对在直缓点处横移量突变增大,在缓圆点处平稳过渡达到最大幅值进入圆曲线段,横移量保持稳定通过曲线段后,一、二、四、五位轮对在圆缓点处突变减小,而三、六位轮对则相反,之后各轮对在直缓点处幅值逐渐趋于稳定,平稳过渡再次进入直线段。
图5(b)所示为各工况轮对横移量幅值对比,由图可知,机车在过曲线时,以Ⅰ端一位轮对横移动态响应最为剧烈,其中又以工况1条件下横移幅值最大达13.49 mm,分别比工况2、3、4条件下横移量大1.33%、3.48%、1.1%;Ⅱ端以四位轮对横移量最大达12.50 mm,不同工况条件下,四位轮对横移量基本一致,五、六位轮对同四位轮对响应特性基本一致,Ⅱ端不同轮对横移动态响应,幅值变化基本不受不均衡闸瓦压力影响,从幅值角度来看,工况1条件下一位轮对潜在安全隐患更大。

图5 各工况轮对横移量对比分析
在轮对横移运动的基础上,从轮对摇头运动角度分析,来反映车辆过曲线时摇头运动规律,初步确定运动状态最剧烈的工况。图6给出了工况1条件下轮对摇头角时程响应及各工况下轮对摇头角幅值对比分析,如图6(a)所示,各轮对在进入圆曲线段前,在直缓点、缓圆点处均突变增大,进入曲线后平稳通过,在出缓和曲线段处又突变减小;根据6(b)可知,在工况1条件下一位轮对摇头角幅值同样为最大幅值达9.42 mrad,分别比工况2、3、4大13.16%、21.23%、13.38%;Ⅱ端四位轮对摇头角幅值最大为7.71 mrad,同横移动态响应一般,Ⅱ端所有轮对在不同工况下摇头角幅值基本未变。
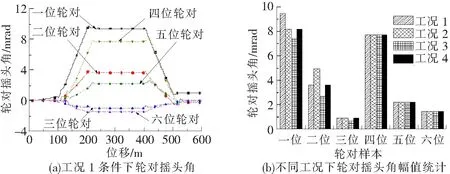
图6 各工况轮对摇头角对比分析
根据以上分析,当轮对只在闸瓦压力作用下,机车通过曲线时,轮对横移、摇头动态响应以工况1条件下,Ⅰ端一位轮对响应最为剧烈,Ⅱ端以四位轮对响应最甚,但是不同工况下对Ⅱ端不同轮对样本横移幅值及摇头角幅值变化并未产生明显影响,故下文着重分析Ⅰ端轮对动态行为规律。
3.2 曲线通过最严重工况分析
上节给出了轮对运动状态分析,从运动状态来看,当出现不均衡制动故障时,故障端位轮对动态响应最为剧烈,下面从轮轨横向力、轮轨垂向力、脱轨系数、磨耗功率等动力学指标分析,给出了不同工况下各指标幅值统计,以此最终确定曲线通过时最严重工况及响应最剧烈车轮。
图7反映了不同工况下轮轨横向力、轮轨垂向力、脱轨系数、磨耗功率幅值统计,由图7(a)和图7(b)可知,各工况下一位外轮轮轨横向力、垂向力响应最剧烈,其中又以工况1条件下一位外轮幅值最大,轮轨横向力及垂向力最大幅值分别达58.57 kN、132.77 kN,工况4一位外轮轮轨横向力幅值达57.26 kN,故障状态下轮轨横向力比正常运行状态下大2.24%,不同工况对垂向动态响应变化并无明显影响,同一车轮样本不同工况下轮轨垂向力无太大差异;根据图7(c)和图7(d)可以看出,不同车轮样本下,脱轨系数与磨耗功率响应最剧烈同样为工况1条件下一位外轮,脱轨系数及磨耗功率最大幅值分别为0.44 kW、10.10 kW,工况4条件下幅值分别为0.43 kW、8.96 kW,两工况脱轨系数差异甚小,故障状态下磨耗功率增大了11.29%,且同一工况下不同车轮样本磨耗功率呈现出单调的线性变化规律。
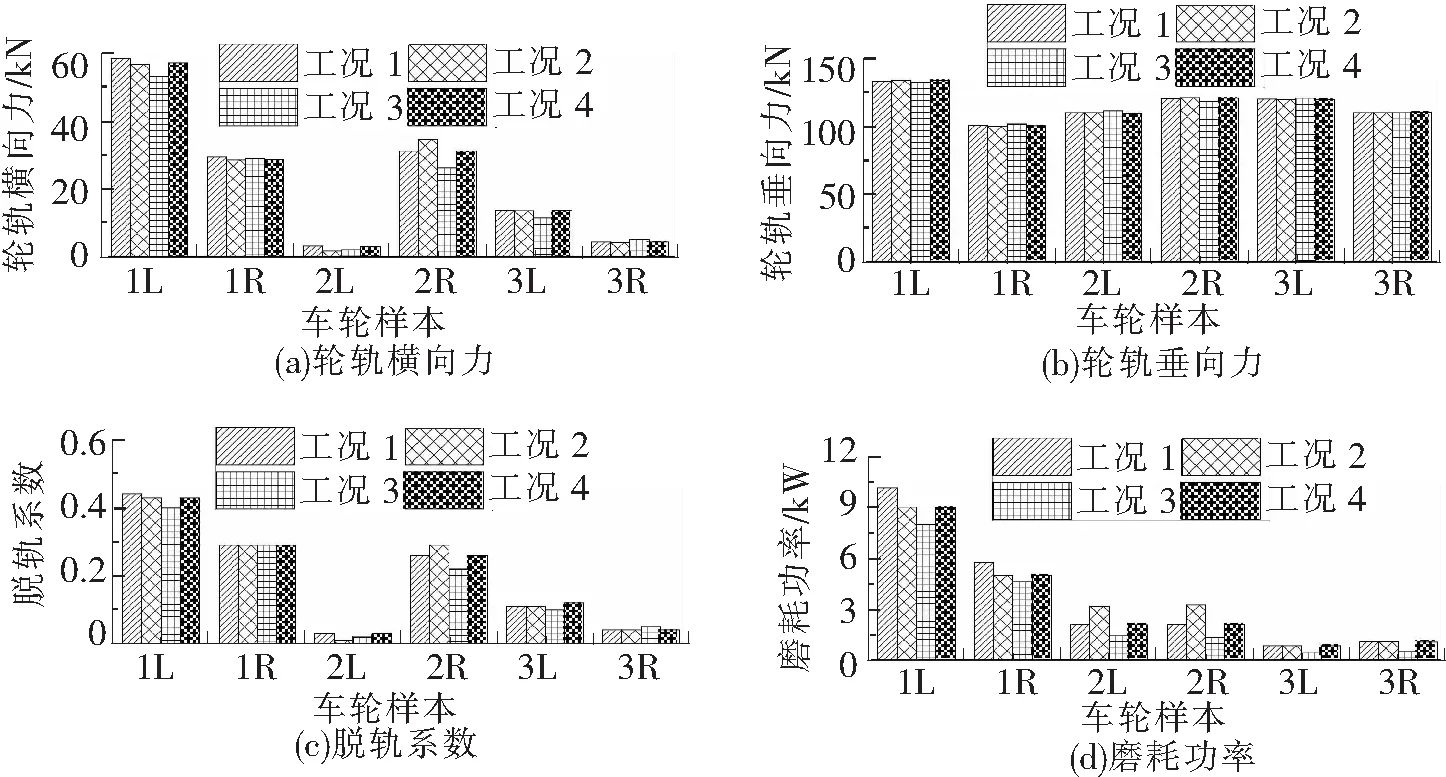
图7 不同工况下考核动力学指标幅值统计
根据上述考核动力学指标幅值统计分析可知,工况1条件下一位外轮动态响应最为剧烈,以下着重分析工况1与正常运行条件下一位外轮时程响应对比,分析线路过渡处动态响应差异变化,由图8可知,所有考核动力学指标均在缓和曲线处幅值发生突变,在圆曲线段平稳过渡;同时又根据图8(d)可知,过曲线时两工况磨耗功率差异最为明显,并结合上节不同工况下磨耗功率幅值统计,可以看出,不均衡制动故障发生,会使磨耗功率增大,呈现较高水平。

图8 考核动力学指标一位外轮时程响应分析
综合上述分析,从轮对横移量、摇头角、轮轨横向力、轮轨垂向力、脱轨系数、磨耗功率分析来看,机车在过曲线时,所有车轮样本中一位外轮动态响应最为剧烈,工况1条件下各动力学指标均是最大幅值;在缓和曲线处轮对动态行为响应变化会产生突变,由于未施加轨道激励,并且实际的运行线路环境更为复杂,故在实际运行中各动力学指标,比仿真数值要大很多,机车端部轮对潜在安全隐患最大。
4 结论
(1)当机车通过曲线时,发生不均衡制动故障,故障端转向架动态响应更为剧烈,且以端部轮对出现故障,是所有轮对中动态响应最剧烈的,在日常的检修维护中,对于端部轮对的检查维护应给予重视。
(2)端轴单元制动器失效状态与正常运行状态相比,轮对横移量、轮轨横向力有微小增幅,增幅分别为1.1%、2.24%,轮对摇头运动水平增加,增幅为13.38%,轮轨垂向力、脱轨系数则相差很小,磨耗功率最大幅值可达10.10 kW,呈现较大水平,同比正常运行状态增加了近11.29%。在同一工况下不同车轮样本中,轮轨横向力、轮轨垂向力、脱轨系数规律变化离散程度较为明显,而磨耗功率则呈现出单调递减的规律;从整体来看,第三位轮对受不均衡闸瓦压力作用影响较小,各工况下考核动力学指标幅值均呈现较小的状态,对不均衡制动敏感性呈现出弱相关表现。
(3)各考核分析动力学指标均在缓和曲线处出现了突变,同时在未施加轨道激励状态下,各动力学指标已经呈现出较大水平,在实际运用中,应尽量避免出现不均衡制动故障。
