基于小波分析的多层框架结构损伤识别研究

丁 科 ，邓宇龙 ，肖运蔚

(1. 中南林业科技大学 土木工程学院，长沙 410004；2. 中南林业科技大学 工程流变学湖南省重点实验室，长沙 410004；3. 湖南建工集团 装饰工程有限公司，长沙 410004)

随着时间的推移，大部分结构在使用过程中会出现不同程度的损伤，尤其是一些结构经常在超负荷的情况下服役，造成了构件或部分结构出现损伤﹒纵使在正常使用情况下，随着服役年限的增加，结构的强度和刚度也会有所下降，当损伤达到一定程度时可导致结构完全破坏﹒因此，及时对结构进行检测和诊断，确定其损伤出现的位置以及损伤的程度，对于维护和确保结构安全可靠是非常必要的﹒

结构出现损伤的根本原因在于组成结构的构件局部强度或刚度降低和质量损失，其在结构动力特性参数上的表现是结构的模态参数发生了改变﹒因此，可以根据系统的动态特性参数来对结构进行损伤定位﹒通常可以根据频率、振型、模态应变能、刚度矩阵、柔度矩阵、频响函数、传递函数等参数来定位损伤位置﹒如Cawley[1]曾经利用结构损伤前后频率的变化来确定损伤位置；Yuen[2]根据结构损伤前后振型与特征值的比值来分析悬臂梁的损伤位置；张勇等[3]认为曲率模态的微分对结构损伤有较高的敏感性；Stutz 等[4]根 据响应面模型和柔度矩阵，运用粒子群优化方法来求解损伤识别逆问题；郑飞等[5]基于单元模态应变能变化率提出了多位置损伤诊断的组合方法；张龙[6]以塑性率作为损伤参数来分析钢筋混凝土框架损伤程度﹒

小波变换是在傅立叶变换(Fourier transform)的基础上发展起来的，克服了其不能作局部分析的不足，广泛地应用于图像处理、语音识别、偏微分方程求解、故障诊断等方面﹒近20 年来，利用小波变换对信号奇异性处理的优点，使其被逐步应用到土木工程结构损伤检测中﹒郭健[7]分析了小波包能量特征提取方法，并通过耦合神经网络法对损伤特征信息进行融合用以确定损伤位置；管德清等[8]曾对运用小波变换对单层平面框架结构的应变模态进行处理，判断框架裂缝位置；李洪泉等[9]运用小波变换的尺度函数来判断结构损伤；Magdalena[10]的研究表明梁高阶模态的小波变换对损伤具有较高的敏感性；杨佑发等[11-12]基于构件损伤后固有频率的一、二阶灵敏度矩，通过混合迭代算法识别损伤位置；杨海鸣等[13]根据小波模极大值分布图来确定结构的损伤位置；鞠彦忠等[14]将小波去噪和小波神经网络相结合进行框架结构的损伤识别﹒

本文主要考虑运用小波变换对2 层框架结构的曲率模态进行处理，并分析不同工况下其对框架结构损伤的识别能力﹒

1 小波变换基本理论

小波变换是20 世纪80 年代发展起来的一种数据处理工具﹒1981 年法国学者Morlet 基于群论思想首次提出小波分析这一概念并成功运用在地质数据分析，由此引起了其他学者的广泛关注和研究﹒1985 年，Meyer 提出了光滑的小波正交基；1986 年，Lemarie 在Meyer 的指导下提出了多尺度分析思想；1988 年，Daubechies 提出一系列具有紧支集的光滑正交小波基﹒此后，在Mallat 多分辨分析基础上形成了快速小波算法，加快了小波变换在实际中的应用﹒

则称 Ψ (t)为小波母函数﹒引入伸缩和平移因子后，小波母函数 Ψ (t)可以写为：

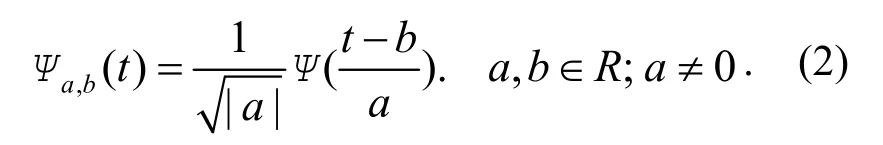
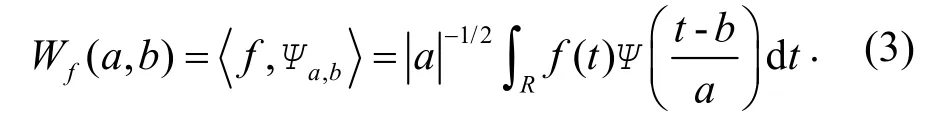
其逆变换为：

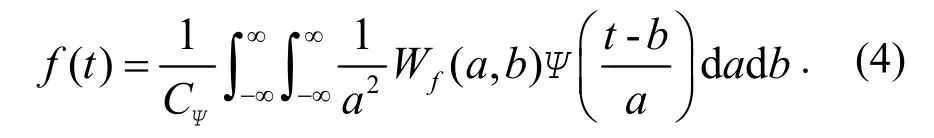
工程中常用于损伤识别的小波函数有：Daubechies 系列小波、Morlet 小波、Symlets 系列小波、Meyer 小波等﹒

2 多层平面框架结构损伤分析

多层平面框架结构作为一个离散的多自由度的系统，其自由振动方程为：

式(6)表示系统无阻尼时的自由振动方程﹒运用有限元分析软件，可以获取结构的各阶振型；然后根据中心差分公式，可以得到第r 阶振型在第i个结点处的模态曲率：

第1 步：运用有限元分析软件计算模型结构的固有频率和振型﹒对于实际结构，可以通过仪器测量其前几阶固有频率和振型﹒

第2 步：根据公式(7)对振型进行计算，得到其模态曲率﹒

第3 步：选择适当的小波类型和分解层数，运用连续小波变换对模态曲率进行分析，根据变换后的小波分解系数判断结构的损伤位置﹒

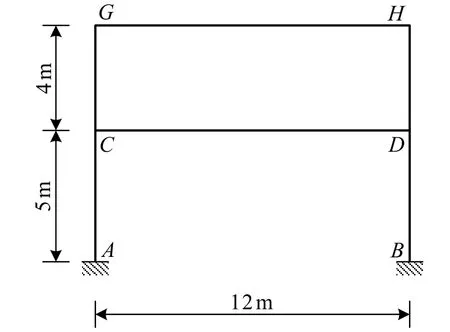
图1 平面2 层框架结构模型

如图1 所示，有一2 层平面框架结构，第1 层层高5 m，第2 层层高4 m，跨度为12 m﹒取混凝土强度等级为C25，梁柱横截面均为矩形，其横截面宽度 b= 0.2 m ，高度 h= 0.3 m，材料弹性模量 E = 3.1 ×1 04MPa，泊松比 μ = 0.2，密度ρ = 2 500 kg/m3﹒取单元长度为10 mm，采用平面刚架单元对该框架结构进行分析﹒现假设该平面框架结构发生损伤，损伤情况如表1 所示﹒

工况一：左边立柱AG 距A 点2 m、7 m 处，右边立柱BH 距B 点6 m 处，横梁GH 距G 点1 m处，横梁CD 距C 点9 m 处共5 处发生损伤，损伤情况如表1 所示﹒运用自编的分析软件，得到其前八阶振型，如图2 所示﹒

表1 框架损伤情况

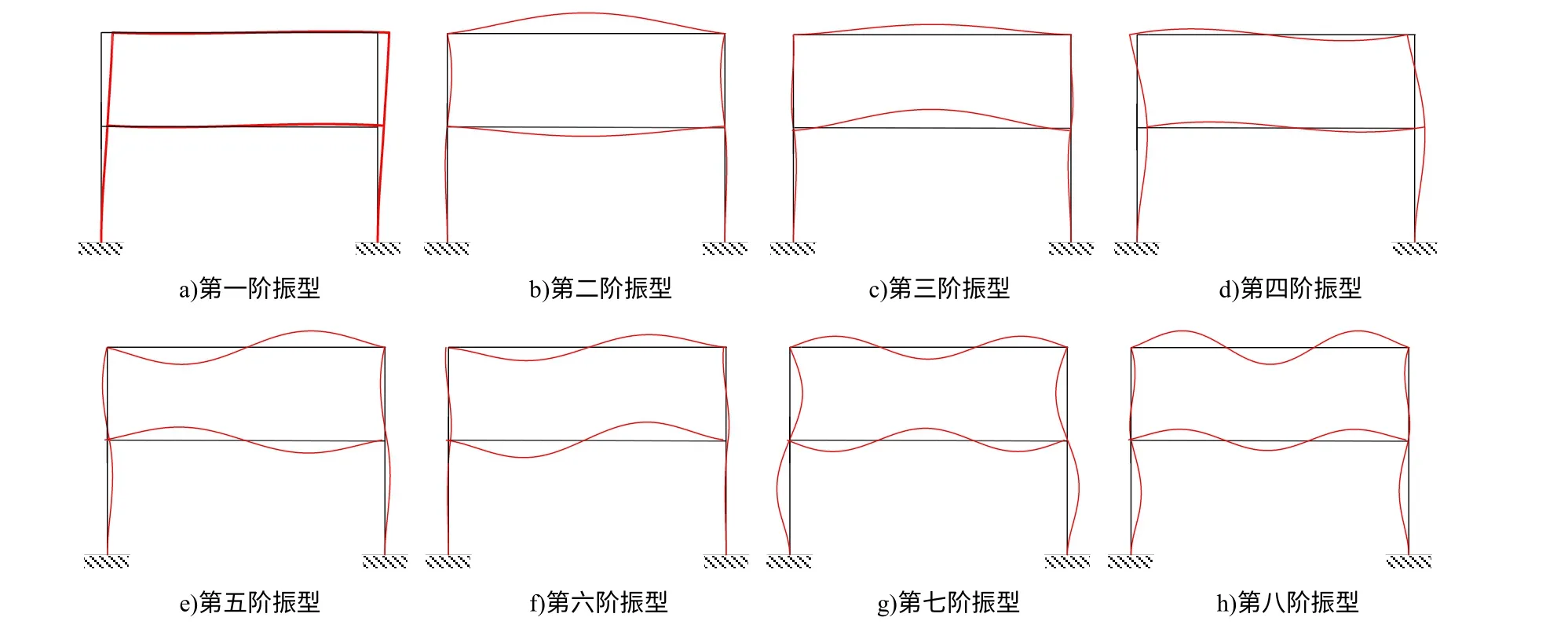
图2 工况一下框架结构的振型

根据公式(6)计算各阶振型的曲率，基于Matlab 平台编制程序对各阶模态曲率进行连续小波变换，本文的小波函数为db3 小波，分解层数为15 层，图3 所示为图2 八阶模态的处理结果﹒

由图3 可以看出，损伤位置处的小波变换系数存在不同程度的模极大值﹒然而，也有部分模态的损伤位置不明显，如图3a)中一阶模态的小波变换在2#、3#损伤位置不明显；图3f)中第六阶模态的小波变换在1#损伤位置不明显﹒故在实际检测中，需要得到结构的多阶模态，综合考虑各阶模态的小波变换系数模极大值﹒

工况二：结构发生2 处损伤，分别为右边立柱BH 距B 点7 m 处损伤35%，横梁GH 距G 点3 m 处损伤30%﹒根据公式(6)计算了前八阶振型的曲率，然后对各阶模态曲率运用db3 小波进行15层小波分解﹒图4为该平面框架在工况二时前八阶模态曲率的小波变换系数﹒由图4 可知，八阶模态的小波变换系数在损伤位置处均存在不同程度的模极大值﹒因此，可以根据小波变换系数确定损伤的位置﹒

工况三：结构发生1 处损伤，为右边立柱BH距B 点3 m 处，损伤40%﹒运用有限元分析软件计算其前八阶振型后根据(6)式计算其各阶振型的曲率，对各阶模态曲率采用db3 小波进行10层连续小波分解﹒图5 为前八阶模态曲率的第10层小波变换结果﹒由图5 可看出，前八阶模态曲率的小波变换系数在损伤位置均存在模极大值﹒

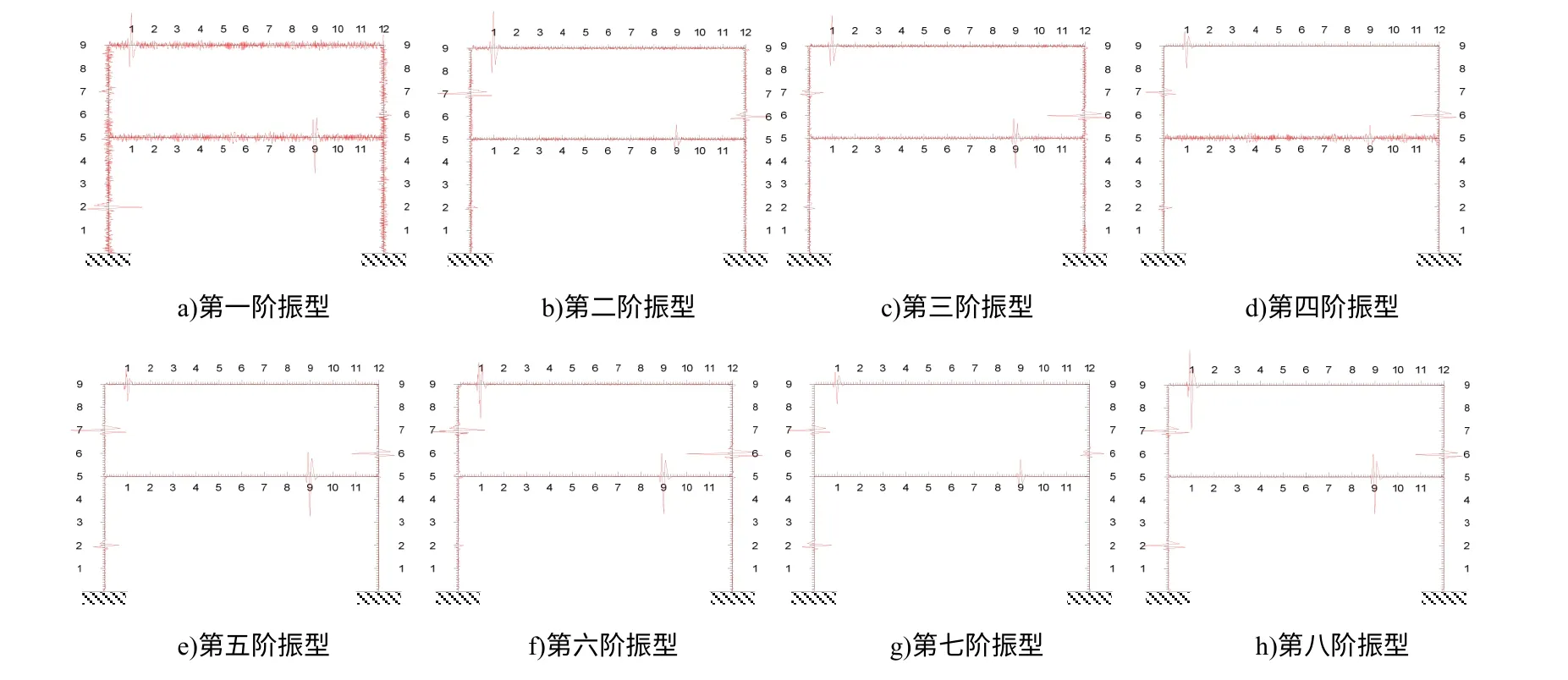
图3 工况一下框架振型的小波变换结果

图4 工况二下框架振型的小波变换结果

图5 工况三下框架振型的小波变换结果

综合3 种情况可知：框架结构发生损伤时，通过对振型的曲率模态进行小波变换，可以根据变换系数的模极大值来定位结构损伤的位置，但模极大值的大小与损伤程度的对应关系不确定﹒

4 结论

1)运用db3 小波对框架结构模态曲率进行15层连续小波分解，其小波分解系数模极大值准确指示了框架结构损伤的位置﹒

2)当损伤位置处于某阶振型的平衡位置时，其小波变换系数对损伤位置的确定不明显，通常为了增加损伤位置判断的准确性，需要前面二、三阶的振型数据﹒

3)结构损伤程度的确定是一个难题，不能根据小波变换系数模极大值来确定损伤程度﹒因此，进一步讨论其它指标来确定结构损伤的程度是必要的﹒