基于多元回归的高铁墩台沉降形变预测分析

许 韬，黄长军, ，赵 鑫

(1. 湖南城市学院 市政与测绘工程学院，湖南 益阳 413000；2. 湖南城市学院规划建筑设计研究院 湖南省城乡生态规划与修复工程技术研究中心/湖南省博士后流动站协作研发中心，湖南 益阳 413000； 3. 湖南有色金属职业技术学院 建筑工程系，湖南 株洲 412000)

随着经济的快速发展，高铁已经成为我国公共交通体系中非常重要的组成部分﹒高铁高速的运行速度，对其设计和施工提出了更高的要求﹒桥梁作为高铁线下工程重要的组成部分，由于受外界因素引发或自身结构的变形都可能存在安全隐患，成为发生灾难性事件的诱因[1]，因此，对高铁桥梁的变形监测则变得至关重要﹒墩台作为桥梁重要的组成部分，其形变在量级上往往呈现出微小的特点﹒高铁墩台在形变监测过程中时常会受到外界条件或者随机噪声的干扰，使得采集到的数据以及后处理预测数据显现出较大的波动，从而给数据分析和后续的变形预测带来较大影响[2]﹒目前，一些预测方法例如灰色理论法，时间序列模型、回归模型等预测模型法在高铁形变预 测中得到应用，然而每种预测方法受其自身模型特点和外界条件的限制，具有一定的适用范围﹒因此，在利用预测模型法时需结合实际工程情况，根据工程实际观测条件，选择合适的预测模型和方法[3]﹒考虑到回归模型构建简单的特点，本文以武广铁路线上位于韶关市浈江区梅村境内的梅村特大桥的30#墩台为研究对象，引入多元回归模型对高铁墩台变形数据分析处理，在顾及温度和荷载对墩台作用基础上，利用Matlab 建立了多元回归预测模型，与传统的GM(1, 1)模型进行对比验证，并对其预测精度进行分析和评价﹒

1 多元回归法

回归分析法是数理统计中最成熟、最常用的一种方法，在进行预测分析方面，其适用于单点分析情况﹒该方法基于对变形观测数据和影响因子进行回归分析以及逐步回归计算分析，由此得到变形与影响因子的函数关系式[4-5]﹒回归分析需要定性地分析变量之间的相关关系，当自变量与因变量存在某种关系时，建立的多元回归模型才有实际预测的意义﹒回归分析模型包括线性回归模型、一元线性回归模型和多元线性回归模型等[4]﹒本文主要介绍多元线性回归分析法﹒

1.1 多元线性回归分析

多元线性回归法是研究因变量与多个自变量之间的不确定关系的基本方法﹒该方法应用于桥梁的变形预测分析就是通过分析变形监测的变形量与环境影响因素之间的相关性来建立模型﹒在多元回归模型中，大多数非线性回归模型可以通过变量的变化转化为线性回归﹒

1.2 回归模型检验

对回归方程的显著性(有效性)进行检验，在选择显著性水平α 后，可用公式(9)检验原假设，假若公式(9)成立，即认为在显著性水平α 下，多元线性回归方程中因变量y 与自变量 x1, x2, …,xm之间存在显著线性关系，方程回归效果显著，反之回归效果不显著﹒

2 实例分析

2.1 工程概况

为了对本文方法进行分析，选择梅村特大桥为研究对象﹒该桥全长2 579.49 m，桥梁为直线桥，连续梁桥墩为29#～32#墩，其中30#和31#墩跨既有京广线，墩身结构为直坡圆端形实心墩，两墩身的高度分别为14 和10 m；基础采用钻孔灌注桩，桩径为1.5 m，最长的桩为43.7 m，最短的桩为13.5 m，按柱桩设计；30#和31#墩为上覆粉质黏土和硬塑的地质条件，地基承载力为190～220 kPa；30#和31#支墩基础处理采用条形混凝土基础，支墩采用C 型钢塔架进行拼装，墩基础表面采用C15混凝土封底，墩台施工完成后4 w用浆砌片石回填至墩台面[8]﹒

2.2 数据来源

本文主要以桥梁的墩台沉降变形进行分析，考虑到温度和荷载对墩台沉降的影响，选取30#墩台沉降监测的18 期数据(观测时间间隔为3 d，数据见表1)，建立多元线性回归预测模型﹒文中以前13 期数据建立预测模型，最后5 期数据作为检验数据﹒为验证本文方法的有效性，以上述数据建立GM(1, 1)模型与本文方法进行比较分析﹒

表1 30#墩台沉降18 期观测数据

2.3 模型建立

本文模型的建立利用Matlab 中的regress 函数进行数据处理和分析[9-10]，其形式如下：

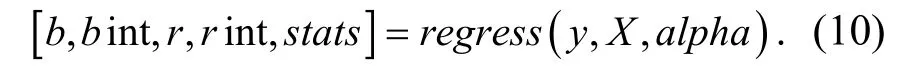
式中，b 为回归方程的参数估计值，b int表示b 的置信区间；stats 输出结果中有3 个系数分别表示相关系数、F 统计量和估计误差方差；y 为因变量；X 为自变量；alpha 为显著性水平(一般取0.05)﹒

在本次桥梁墩台沉降监测中主要考虑监测期内的荷载以及温度对桥梁变形的影响，通过绘制出的荷载与累计沉降量的关系图(见图1)可以发现，荷载与沉降量具有一定的线性关系﹒令X1为荷载、X2为温度作为自变量，Y 为累计沉降量，建立二元线性回归模型﹒

图1 荷载与累计沉降量关系

图2 残差分布

通过13 期观测数据建立的残差分布图(见图2)可看出，每个观测值基本都处于其置信区间内， 但第5 个观测值的置信区间未通过原点，该点可视为异常点，需要将该点进行去除后进行插值补充﹒本文采用拉格朗日插值法获得第5 组数据的沉降量，计算插值结果为−2.47 mm﹒将插值获得的数据进行回归分析，利用rcoplot( r,rint)命令得到相应的残差及其置信区间，见图3﹒

图3 去除异常点后残差分布

由图3 可见相应的残差都在其置信区间内，最大残差为−0.422 mm，最小残差为0.022 mm，残差绝对值的均值为0.199 6 mm，残差相对较小，由此说明模型的预测精度良好﹒最终获得桥梁墩台沉降实际值与回归模型预测曲线，见图4﹒

图4 墩台沉降实际值与回归模型预测曲线对比

从图4 可看出，回归模型的预测值与实际值较接近，但第7 和第8 期数据稍微存在偏差﹒从这2 期的原始观测数据来看，可能是由于受到外界其他因素(如暴雨等)影响而造成该点出现了上升的趋势，从第9 期开始，该点又回归到自然的形变状态﹒从较差来看，最小较差仅为0.022 mm，最大较差为0.422 mm，沉降曲线基本与实际相似，说明回归模型在整体上的预测是基本可靠的﹒

表2 回归模型检验相关数值

表2 为计算得到的回归模型检验结果，R 用 来衡量自变量x 与y 之间相关程度的大小﹒R 的值越接近于1，说明拟合得越好，结果表明自变量与因变量之间的关系为高度正相关，拟合优度较高﹒F 显著性统计量为145.731 7，P 值(弃真概率)为4.02×10−8，远小于显著性水平0.05，说明该回归方程回归效果显著﹒回归标准差为0.243 9 较为接近0，说明模型预测值相对于实际沉降量的偏差较小，模型的预测精度较高﹒同时对于 X1的弃真概率为 3.44×10−8， X2的弃真概率为2.77×10−4，两者都远小于显著性水平0.05，但 X1的弃真概率远小于 X2的，说明荷载为影响墩台沉降的主要因素，温度对于墩台沉降变形的影响相较于荷载来说是较小的﹒

2.4 精度分析与讨论

为验证本文方法的有效性，采用前13 期观测数据，利用Matlab 编程建立GM(1, 1)预测模型，将GM(1, 1)模型计算的13 期预测值与回归模型预测值进行比较，2 种预测模型前13 组数据预测曲线和残差绝对值分别如图5 和图6 所示﹒

图5 2 种预测模型前13 组数据预测曲线

图6 2 种模型残差绝对值(前13 组)对比

从图5 和图6 可以看出，GM(1, 1)模型的残差绝对值的均值为0.503 9 mm，而回归模型的仅为0.199 6 mm，相较而言，回归模型的残差比GM(1, 1)模型的小，说明回归模型的预测值更接近于实际沉降量，预测精度更高﹒

为再次验证本文方法的可靠性，利用建立的模型，分别计算出最后5 期的沉降变形量，2 种模型对最后5 期的预测结果分别见图7 和图8﹒

图7 2 种模型后5 组预测数据对比

综上可知，在最后5 期的预测中GM(1, 1)模型的最大残差达到了3.252 mm，最小残差为1.004 mm；在回归模型中最大残差为−0.354 mm，最小 残差为−0.022 mm﹒回归模型的残差绝对值都在0～0.4 mm 之间，残差较小说明预测值与实测值很接近﹒通过以上数据计算可得GM(1, 1)模型最后5 组预测值的残差均值绝对值为2.072 8 mm，回归模型的最后5 组预测值的残差均值绝对值为0.178 8 mm﹒通过对比2 组数据可看出回归模型的预测精度要高于GM(1, 1)模型﹒回归模型的预测曲线与实际沉降曲线更接近，而灰色模型的预测值与实际存在较大偏差﹒由此可见，在此工程案例中，回归模型更适合预测墩台沉降变形﹒

图8 2 种模型残差绝对值对比

3 结论

本文以梅村特大桥为研究对象，通过对桥墩墩台的沉降监测，得到原始观测数据﹒在对墩台沉降进行多元回归分析中，主要考虑了温度和荷载对其的影响，然而，在实际的工程应用中，墩台的形变会受到诸如水文地质、风力作用、土壤的物理性质以及湿度等多种因素的共同作用﹒为了得到更加精确的预测成果，需要从多方面考虑影响墩台变形的因素，以便对桥梁整体变形进行准确的预测﹒根据原始观测数据序列建立了基于墩台沉降的二元线性回归分析模型，由于在实际工程中桥墩的沉降会趋于稳定，而二元线性回归模型中如果荷载一直增加则沉降预测值将会越来越大，这与实际情况相违背﹒因此，当桥墩沉降趋于稳定之后，二元线性回归模型在后期的变化中不再适合用来进行沉降预测﹒

在本文分析的数据中，由前13 组数据建立模型，后5 组数据作为模型检验数据，当建立模型的数据选取不同时，模型精度也会有所改变，如减少原始样本，回归模型的精度可能会降低﹒此外，本文选取的二元线性回归模型过于单一，为了提高预测精度，可以选择多种方法结合的组合模型，如多元线性回归+时序分析、多元线性回归+BP 神经网络模型以及多元线性回归+趋势分析等进行数据分析处理，以建立更加精确的变形预测模型，提高整体的预测精度﹒