外延PbZr0.4Ti0.6O3薄膜厚度对铁电储能性能的影响

2020-07-18宋建民

人工晶体学报 2020年6期

董磊，赵磊，宋建民,

(1.河北农业大学理学院，保定 071001；2.河北大学物理科学与技术学院,保定 071002)

0 引言

铁电薄膜材料因同时兼具高能量密度和高功率密度，可被广泛应用于脉冲电力系统、电动汽车、高频逆变器等领域，引起了众多科研工作者的广泛关注[1-4]。PbZr1-xTixO3(PZT)基薄膜因具有大的极化强度，高的击穿强度，制备工艺简单，易于成熟的半导体工艺集成等特点，现已成为铁电薄膜储能首选材料之一[5-7]。众多实验研究表明，具有高质量外延取向结构的薄膜具备更优的铁电性能[8-10]。PZT与SrTiO3、LaAlO3、MgO等材料具有相近的晶格匹配常数，因此，高质量外延取向PZT薄膜可以在这些基底上沉积获得[11-14]。Chu等[15]实验研究发现，在外延异质结PZT/SrTiO3中，PZT的铁电性能与基底的失配位错、应力场以及薄膜的厚度密切相关。Wang课题组[16]利用热力学朗道理论研究了对(001)取向的PbZr0.4Ti0.6O3薄膜铁电性能的影响，结果表明铁电性能对厚度的依赖性是该厚度下位错和弹性应变共同作用的结果。然而至今，利用热力学朗道理论系统研究薄膜厚度对PbZr0.4Ti0.6O3储能性能的影响报道较少。基于此，本文通过修正的Landau-Devonshine理论，考虑位错应力场和极化场之间的耦合，建立外延PbZr0.4Ti0.6O3/SrTiO3异质结的热力学模型，研究在SrTiO3衬底上外延生长的PbZr0.4Ti0.6O3薄膜的铁电性能和铁电储能性能对其厚度的依赖关系，为高性能铁电储能器件制备与设计提供实验参考和理论依据。

1 理论基础

1.1 Landau-Devonshire相变自由能公式

建立空间直角坐标系：x//[100]，y//[010]，z//[001]，薄膜平面为xy平面，极化方向平行于z轴。当仅存在内应力时，顺电相的立方结构PZT经冷却变到铁电相的四方结构，其Landau-Devonshire相变自由能G(T,P,σij)为

G(T,P,σij)=G0+a1P2+a11P4+a111P6-EP+u11σ11+u22σ22+u33σ33+u12σ12+u13σ13+u23σ23

(1)

式(1)中，G0表示顺电相自由量；a1，a11和a111为PZT的刚性系数；σij为内应力；uij为内应变；E为外加z方向电场强度；P为极化强度；T为热力学温度。a1与T之间满足如下式关系

(2)

式(2)中，TC和C分别是块体材料的Curie-Weiss温度和Curie-Weiss常数；ε0是真空介电常数。

1.2 薄膜厚度与铁电储能密度的关系

考虑到PZT/STO结构，则晶格失配度为

(3)

式(3)中，a0与as分别表示PZT与STO的晶格常数。晶格失配会引起PZT薄膜在界面形成位错。根据Matthews-Blakeslee理论可以得到形成位错的临界厚度hρ满足的等式[5]

(4)

式(4)中，ν为Poisson比，且满足ν=|S12/S11|，Sij表示PZT的弹性顺度系数；b0为xz平面上刃位错的Burgers矢量b=a0[100]的强度|b|。

PZT/SrTiO3的电滞回线随厚度的变化关系，可以通过Alpay等[17]的方法得出。当PZT薄膜厚度小于临界厚度hρ时，由(1)式可以推得自由能G(P,E)所满足的方程为

(5)

xm=-f

(6)

(7)

(8)

式(5)、(7)和(8)中，Sij和Q12分别为PZT的弹性顺度系数和电致伸缩常数。

当存在外电场E作用时，系统达到平衡需满足∂G/∂P=0条件，从而由式(5)可以得出P和E所满足的方程为

(9)

(10)

(11)

式(11)中，ρ表示位错密度，且满足

(12)

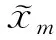
铁电薄膜储能中，总储能密度(W)、有效储能密度(Wrec)和储能效率(η)的计算公式[4]如下：

(13)

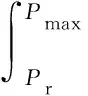
(14)

(15)

式(13)、(14)和(15)中，P、Pmax、Pr与E分别为极化强度、极大极化强度、剩余极化强度与施加的电场强度。Wrec的值可通过计算图1中D区域(深色阴影部分)面积得到；W的值可通过计算图1中D区域面积与L区域(浅色阴影部分)面积的和得到。

2 结果与讨论

表1给出了PbZr0.4Ti0.6O3的典型参数[18-20]。

表1 PbZr0.4Ti0.6O3典型参数Table 1 Typical parameters for PbZr0.4Ti0.6O3

注意到SrTiO3的晶格常数为0.390 5 nm，考虑沉积在SrTiO3衬底上的铁电薄膜PbZr0.4Ti0.6O3，将表1参数代入式(4)，可得PbZr0.4Ti0.6O3薄膜产生刃型位错的临界厚度为hρ=1.27 nm。这样，当薄膜厚度h大于临界厚度1.27 nm时，式(9)中的系数改写为

(16)

(17)

将式(17)中的参数带入式(9)可得

aP5+bP3+cP-E=0

(18)

式(18)中c是关于薄膜厚度h的函数，由此可以得出电场强度E和极化强度P与h的关联函数。根据式(18)并结合式(13)、(14)和(15)可以得到Pr、Pmax、Ec、W、Wrec和η与PbZr0.4Ti0.6O3薄膜厚度h的函数关系式

(19)

(20)

(21)

W=PmaxEc

(22)

(23)

式(19)～(23)中，参数P0和x1～x6均为h的函数，分别表示为

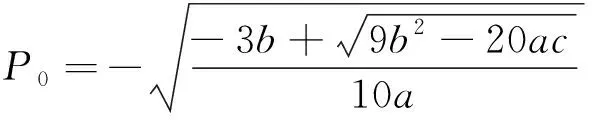
将表1中对应的参数代入以上各式，可以得到剩余极化强度Pr、极大极化强度Pmax、矫顽电场强度Ec、总储能密度W、有效储能密度Wrec与储能效率η随PbZr0.4Ti0.6O3薄膜厚度h的函数。本文的主要目的是解析上述函数随薄膜厚度h的变化情况。

2.1 Pr、Pmax与Ec随薄膜厚度h的变化情况

通过方程(19)、(20)与(21)，得到剩余极化强度Pr、最大极化强度Pmax与矫顽电场强度Ec随PbZr0.4Ti0.6O3薄膜厚度h的变化曲线，如图2(a)、(b)与(c)所示。由曲线可以看出，Pr、Pmax与Ec均随PbZr0.4Ti0.6O3薄膜厚度h的增加而呈非线性增大。薄膜厚度在1.27 nm到25.0 nm范围内，Pr、Pmax与Ec的值变化较快，当薄膜厚度达到约为60.0 nm左右时，Pr、Pmax与Ec趋于饱和。通过图2(a)、(b)与(c)曲线可以读出，幅度达到99%，即Pr、Pmax与Ec的值分别为75.3 μC·cm-2、84.1 μC·cm-2与2 240.7 kV·cm-1时，对应的厚度分别为57.0 nm、57.0 nm与64.2 nm，这表明PbZr0.4Ti0.6O3薄膜厚度达到65.0 nm时，铁电性能基本达到饱和。

2.2 W、Wrec与η随薄膜厚度h的变化情况

根据图2中的Pr和Pmax结果，并结合方程(22)、(23)与(15)，可以得到总储能密度W、有效储能密度Wrec与储能效率η随薄膜厚度h的变化曲线，如图3(a)、(b)与(c)所示。由图3(a)和(b)中曲线可以看出，总储能密度W和有效储能密度Wrec随PbZr0.4Ti0.6O3薄膜厚度h的增加而呈非线性增大，趋势与Pr、Pmax和Ec变化相似。薄膜厚度在1.27～25.0 nm范围内变化较快，当PbZr0.4Ti0.6O3薄膜厚度h分别增大到66.0 nm和65.8 nm时，幅度达到了99%，对应的总储能密度和有效储能密度分别为188.5 J·cm-3和9.0 J·cm-3。然而，储能转换效率η与总储能密度W和有效储能密度Wrec恰好相反，其值随h的增加而呈现了非线性减小，如图3(c)所示。当薄膜厚度接近52.6 nm时，η趋于一稳定值4.79%。由于SrTiO3衬底与PbZr0.4Ti0.6O3存在晶格失配导致PbZr0.4Ti0.6O3在界面处产生应力，破坏了晶格的周期性分布，刃形位错密度形成，从而降低了铁电性能。随着厚度的增加，应力对PbZr0.4Ti0.6O3薄膜的作用减弱，刃形位错密度减小，结晶质量提高，铁电性能对应提升。以上理论计算结果所显示的Pr、Ec和Wrec在厚度约为66.0 nm时基本达到饱和，说明PbZr0.4Ti0.6O3薄膜厚度大于66.0 nm时，应力对其铁电性能的影响可以忽略，这与Alpay等[21]报道的结果相似。