基于逻辑思维图的大数定律教学研究
2020-07-17王燕飞金玉子
王燕飞,金玉子
(吉林化工学院 理学院,吉林 吉林 132022)
著名的德国思想家恩格斯曾经说过,在表面上体现出来的偶然性实质是内部的必然性在起作用。概率论与数理统计就是通过看似偶然的随机现象,研究其内在必然的统计规律性,这需要探讨试验次数趋于无穷大时的极限情况。大数定律和中心极限定理正是透过大量随机现象所呈现出来的两个极限理论。它们在整个概率论与数理统计课程中占有非常重要的地位,是现代概率论、统计学、理论科学和社会科学的基石。大数定律以严格的数学形式体现了随机现象最根本的性质之一:平均结果的稳定性。它是随机现象统计规律性的具体表现,是概率论的中心课题之一,它的解决标志着测度论在概率论研究中的有力渗透,成为概率论公理化的前奏。
目前,针对大数定律这部分内容,大多数教材及教学研究,都只是围绕伯努利、切比雪夫、辛钦这三个大数定律,很少有人提及泊松和马尔可夫这两个大数定律的结果[1-8]。事实上,从发展历史的角度来看,后者也是必不可少的,特别是研究5个大数定律之间错综复杂的也是至关重要的。为此,本文首先按照历史沿革的顺序分别介绍5个大数定律的满足条件、产生背景及其应用价值。然后利用逻辑思维图的方法分析它们的之间的关系。拓宽该知识点的宽度、广度和深度,从而为教师提供清晰明朗的讲解思路,也使得学生对该部分内容更容易理解透彻,掌握得更加扎实。另外,从课程思政[9]的角度挖掘大数定律的深刻意义。
一、大数定律的一般形式
首先,我们先来了解一种特殊的收敛,由此定义大数定律的结果。
(一) 依概率收敛
若随机变量序列{Xn}满足:对于任意小的正数ε>0,有:
(1)
或者
(2)
依概率收敛是一种从概率的角度刻画的收敛[10]。它指的是当n充分大时,Xn与X的距离任意小这一事件的概率几乎接近于1,等价于其对立事件的概率几乎接近于0。概率接近0,但仍有可能发生,只是发生的概率很小而已。
(二) 大数定律的定义
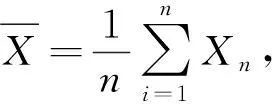
(3)

二、常见的大数定律
对于一个随机变量序列来说,我们比较关心的是,在什么情况下,随机变量序列才能服从大数定律呢?为此,统计学家们不断探索研究,得出了很多种条件,其中比较著名的有5种。下面我们按照大数定律的发展历程分别介绍它们满足的条件。
(一) 伯努利大数定律
在n重伯努利试验中,设ηn为n次试验中事件A发生的次数,P(A)=p,则有:
(4)
即A发生的频率依概率收敛于其概率值。它以严格的数学形式表达了“频率稳定于概率”这一看似显而易见的事实。这一结果是由概率论的先驱人——瑞士数学家伯努利,在1713年出版的《猜度术》中提出并证明的。它是有史以来的第一个大数定律。它的出现无论是理论还是应用都具有重要意义,其影响深远,至今未衰。由于其极端重要性,1913年12月彼得堡科学院举行了庆祝大会,纪念这一结果诞生200周年。
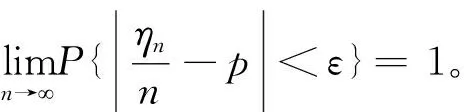

图1 伯努利大数定律的直观演示图
伯努利大数定律为概率的统计定义提供了强有力的理论依据,使得我们可以如此理直气壮地利用频率近似概率。而这样的应用也极为广泛。比如:
在蒲丰投针试验(图2)中,主要的解决思路就是用大量投针试验的针与线相交的频率近似其概率值,从而求得π的近似值。
后来,人们利用计算机模拟所设计的试验,以事件出现的频率估计事件的概率,并将其作为问题的解。这种方法就是著名的蒙特-卡罗法,它广泛地应用于金融工程学,宏观经济学,生物医学,计算物理学等领域。
在学习数学期望的定义时,我们知道,当随机变量取值个数为有限时,算术平均值等于取值乘以频率的加权和.将以频率作为权重替换为以概率作为权重,从而获得了随机变量更为稳定的平均值——数学期望。
后来,法国数学家泊松将n重伯努利试验修改为n次独立试验,使得每次试验A发生的概率可能不同,进而得到了条件更为一般的泊松大数定律。
(二) 泊松大数定律
在n次独立试验中,设ηn为n次试验中事件A发生的次数,第i次试验中A发生的概率为pi(i=1,2,…,n),则有:
(5)
著名的俄罗斯数学家切比雪夫严格地证明了伯努利和泊松两个大数定律。1866年,他发表了《论平均数》这篇论文,从切比雪夫不等式出发,得到了切比雪夫大数定律。
(三) 切比雪夫大数定律
若随机变量序列{Xn}满足:两两不相关,且∃C>0,D(Xn)≤C(方差一致有界)。则{Xn}服从大数定律。
在概率论门户萧条的年代里,切比雪夫的工作无疑起到了振聋发聩的作用。但是由于处理手法还不够完善,所得结果还是比较粗糙的。后来,他的得意弟子马尔可夫,经过努力找到了更为合理的条件,这就是马尔可夫大数定律。
(四) 马尔可夫大数定律
若随机变量序列{Xn}满足:
(6)

(五) 辛钦大数定律
现代概率论的奠基人之一,前苏联数学家辛钦研究出了闻名于世的辛钦大数定律。
若随机变量序列{Xn}满足:独立同分布,且E(Xn)=μ,则{Xn}服从大数定律。即
(7)
这一结果表明,平均值“稳定”于期望值,这种“稳定”指的是从概率的角度刻画的。当n很大时,随机变量在n次观察中的算术平均值以较大的概率接近于它的数学期望值。将它推广的结论,即“总体矩依概率收敛于样本矩”,是后续数理统计部分中矩法估计的重要理论依据。
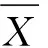
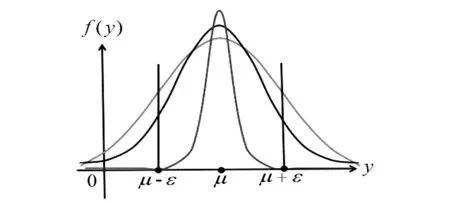
图3 辛钦大数定律的直观演示图
辛钦大数定律为寻找随机变量的期望值提供了一条实际可行的途径,即可以用多次取值的平均值来近似期望值。事实上,在生活中,我们已经不知不觉应用这一理论解决了很多实际问题。比如,在测量身高时,可以用多次测量结果的平均值作为身高的近似值。在竞技比赛中,通常我们用多个评委打分的平均值来反映选手的真实水平。另外,在保险领域,我们用大量投保人所能获得平均赔偿金额作为其需要缴纳的纯保费。
在这5个大数定律中,通常要求重点掌握伯努利、切比雪夫和辛钦这3个大数定律,而对于泊松和马尔可夫两个大数定律,只要求简单了解。
三、常见大数定律之间的关系
这5个大数定律之间有千丝万缕的联系,下面我们进行两两比较,从而得出它们之间的逻辑关系图(见图4)。
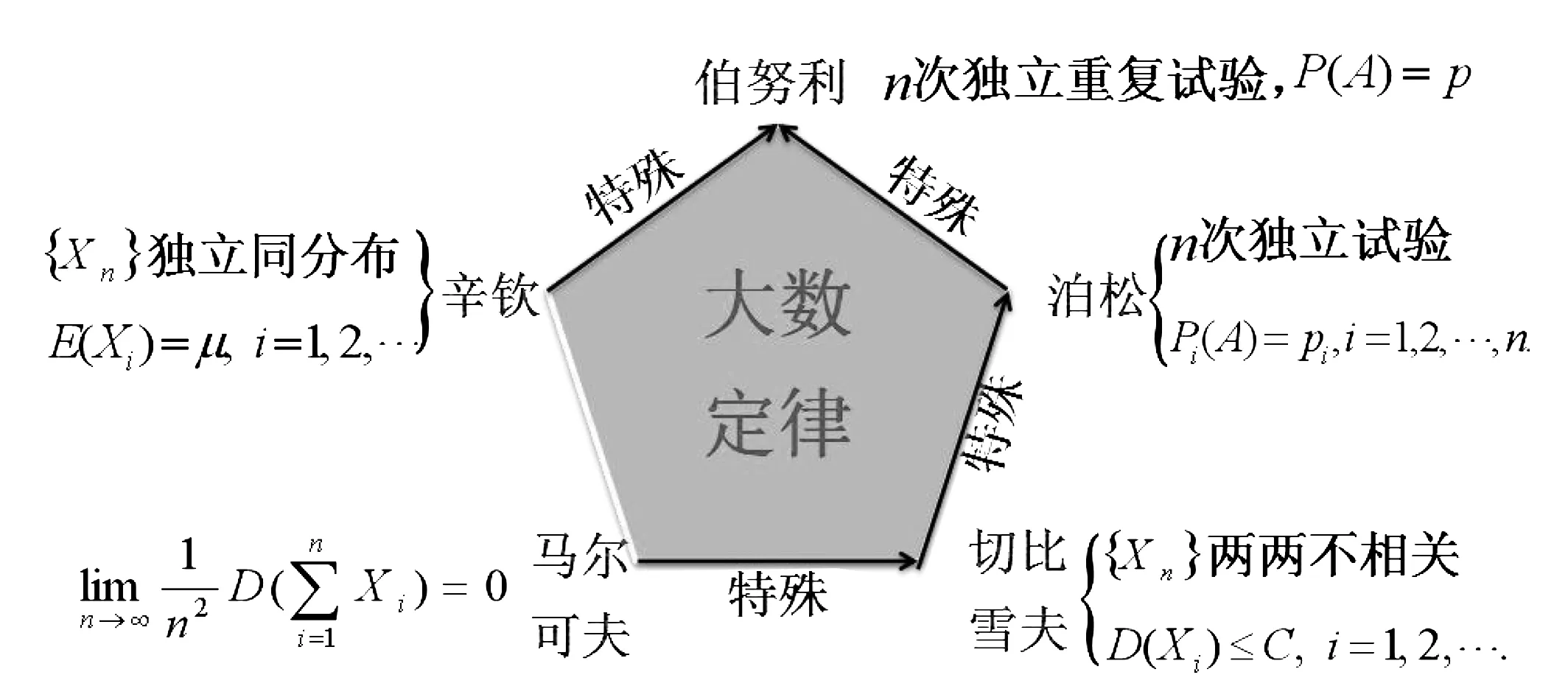
图4 大数定律的逻辑关系图
伯努利大数定律要求在n次独立重复试验前提下,每次试验A发生的概率同为p。在这里,事件A发生的次数ηn可以看作为n个服从(0-1)分布且相互独立的随机变量之和。即
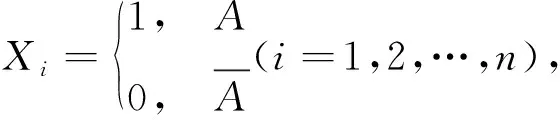
泊松将前提条件修改为第i次试验中A发生的概率为pi,即各次试验概率不同,显然条件更一般。因此,伯努利大数定律是泊松大数定律的特殊情况。
将切比雪夫大数定律的前提条件和泊松大数定律相比较,“两两不相关”弱于“相互独立”。另外,在独立试验中,由于
满足方差一致有界。因此,泊松大数定律是切比雪夫大数定律的特殊情况。
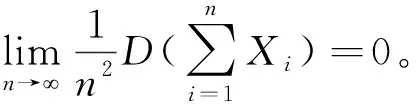
同时去掉了“两两不相关”的条件。所以,切比雪夫大数定律是马尔可夫大数定律的特殊情况。
与马尔可夫大数定律的前提条件相比,辛钦要求“随机变量序列独立同分布”这个条件比较强,而只要求“期望存在”,弱于方差存在的条件,故而二者不作比较。
最后,伯努利大数定律显然满足辛钦大数定律的两个条件,即伯努利最特殊。
综上所述,伯努利、泊松、切比雪夫、马尔可夫这4个大数定律,一个比一个更一般,它们的证明都可以利用切比雪夫不等式作为工具。关于辛钦大数定律的证明则需要借助特征函数理论。在这5个大数定律中,伯努利大数定律是泊松、切比雪夫、马尔可夫和辛钦大数这4个大数定律的特殊情况。
四、 结 语
(1) 大数定律作为概率统计的重要极限理论,其本质含义即为大量随机变量的平均结果具有稳定性。这使得我们对于看似捉摸不定的随机现象似乎有了内在的把握。
(2) 这种概率思想在很多领域的问题中都有所体现。比如,物理学告诉我们,一杯水中的每个水分子的运动是随机的,但整体却呈现出稳定的状态;经济领域中,价值规律的表现形式,正是价格上下波动而稳定于价值。
(3) 将这样的思想应用到哲学中,可以思考,人的一生是起伏不定的,但总体来看,得失也是趋于平衡的。如此看来,我们应该遇到挫败时不气馁,好运来时不骄傲,正所谓“不以物喜,不以己悲,荣辱不惊,淡定人生。”这一点正是“大数定律”带给我们的课程思政元素。
