一种自适应非负矩阵分解算法

李 鑫, 张 伟, 张 蕾

(1. 吉林大学 校长办公室, 长春 130012; 2. 吉林大学 发展规划处, 长春 130012)

非负矩阵分解(nonnegative matrix factorization, NMF)是一种简洁高效的矩阵分解算法[1]. 该算法是在矩阵中所有元素均为非负约束下的矩阵分解方法, 目标是使分解后的所有分量均为非负值并实现非线性维数约减[2]. 由于该算法不需要训练样本, 能自动发现数据中潜在的主题和基向量, 因此非负矩阵分解模型及其改进算法已广泛应用于图像处理[3]、 基因功能预测[4]、 推荐系统[5]和文本挖掘[6-7]等领域. 虽然非负矩阵分解具有简便性、 结果可解释性及空间算法复杂度低等优点, 但传统非负矩阵分解在求解过程中, 基向量矩阵和系数矩阵均需利用随机函数初始化, 基向量数目和最大迭代次数均需专家指定或通过大量实验进行确认. 文献[3]和文献[8]为解决随机性问题, 设定了常数阈值并将迭代求解后求得的平均值作为最终结果, 在文本数据和急性髓细胞白血病数据分析上取得了较好的效果, 但上述方法均未考虑算法最大迭代次数对结果的影响, 而最大迭代次数参数选择不当会降低基向量的代表性. 因此, 本文提出一种基于梯度下降的自适应策略, 并将其引入到非负矩阵分解方法中. 同时, 提出一种自适应非负矩阵分解算法(self-adaptive nonnegative matrix factorization, SANMF). 实验结果表明, SANMF算法与传统非负矩阵分解算法相比增强了鲁棒性, 提高了分解的精度.

1 非负矩阵算法

经典非负矩阵分解算法描述为： 对任意给定的一个非负矩阵V∈F×N, 求解非负矩阵W∈F×T和H∈T×N, 使得

VF×N≈WF×T×HT×N.

(1)

非负矩阵分解是个NP难问题. 因此, 求解可简化为优化问题用迭代方法交替求解W和V. 令E表示重构矩阵与原始矩阵V之间的误差矩阵, 利用最大似然法求解, 即对下列目标函数取最小值:

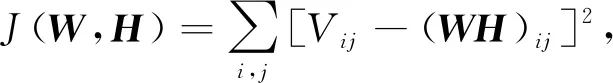
(2)

其中,i和j分别表示矩阵中的行数和列数.W和H在NMF求解过程中的更新规则[9]为

(3)

文献[3]和文献[8]在分析文本数据和急性髓细胞白血病数据时, 将最大迭代次数和基向量数目设为常数, 但当处理不同规模和不同类型的数据时, 固定的常数阈值无法满足实际需求.

2 自适应非负矩阵分解算法

2.1 梯度下降自适应策略 为降低经典非负矩阵分解算法的最大迭代次数q对实验结果的影响, 本文提出一种基于梯度下降的自适应策略. 该策略引入两个与原始矩阵V中行数F相关的阈值变量, 分别为上界(θUp=2F)和下界(θDown=F). 则NMF算法中最大迭代次数求解过程通过引入约束简化为有限域上的求解. 梯度下降自适应求解策略公式为

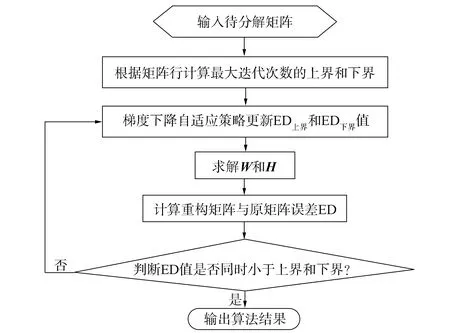
图1 自适应非负矩阵分解算法流程

EDt+1=NMF(qt),

(4)

(5)

(6)

(7)

其中: NMF(q)表示以q为最大迭代次数的传统非负矩阵方法;t为求解NMF的当前迭代次数. 该方法能迭代求解出合适的NMF最大迭代次数.

2.2 SANMF算法 自适应非负矩阵分解算法流程如图1所示. 算法输入为待分解的非负矩阵, 算法步骤如下：

1) 根据矩阵行数确认上界和下界；

2) 根据梯度下降自适应策略, 用式(4)～(7)更新上下界;

3) 用式(3)计算得出W和H;

4) ED=V-WH;

5) 比较ED和ED上界(q取上界时ED的值), ED下界(q取下界时ED的值), 如果ED同时小于ED上界和ED下界, 则表示SANMF算法结束, 输出结果; 如果ED仅小于ED上界, 则用当前ED替换ED上界, 迭代执行步骤2)梯度下降自适应策略, 同时在步骤2)中更新程序存储的ED上界值； 如果ED仅小于ED下界, 则迭代执行步骤2)梯度下降自适应策略, 并用当前ED值替换ED下界值, 同时在步骤2)中更新存储的ED下界值;

6) 输出算法运行结果ED,W和H.

3 实 验

为检验算法的有效性, 实验发现学生中潜在的学习团体, 收集并整理吉林大学某学院264名学生2014—2018年度319门课程的成绩, 课程包括基础课、 必修课和选修课等, 其中五分制的课程评分全部折算为百分制(0～100分). 由于学生成绩矩阵中包含选修课成绩, 而通常情况学生选修课课程分布较广, 所以成绩矩阵中包含大量0元素. 经统计确认课程中的13 429个成绩为0分, 矩阵中0元素百分数为15.9%. 这些0元素所在向量直接影响了数据分析的结果, 运用非负矩阵分解可发现基向量, 从而有效减少稀疏向量的影响. 而直接用经典算法(NMF)分解得到的矩阵误差较大, 因此, 本文将自适应非负矩阵分解模型用于该数据分析中.

图2为自适应非负矩阵分解算法(SANMF)与经典算法(NMF)的比较结果, 其中基向量数量为6. 由图2可见, 二者的聚类结果存在一定的差异. ED为重构矩阵与原始矩阵之间的欧氏距离, 该值越小说明重构矩阵与原矩阵之间的差距越小. 自适应非负矩阵分解算法得到的重构矩阵误差比经典非负矩阵分解算法降低了20.16%, 因此, SANMF算法优于传统NMF算法.

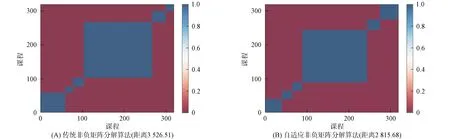
图2 传统非负矩阵分解算法与自适应非负矩阵分解算法聚类结果比较

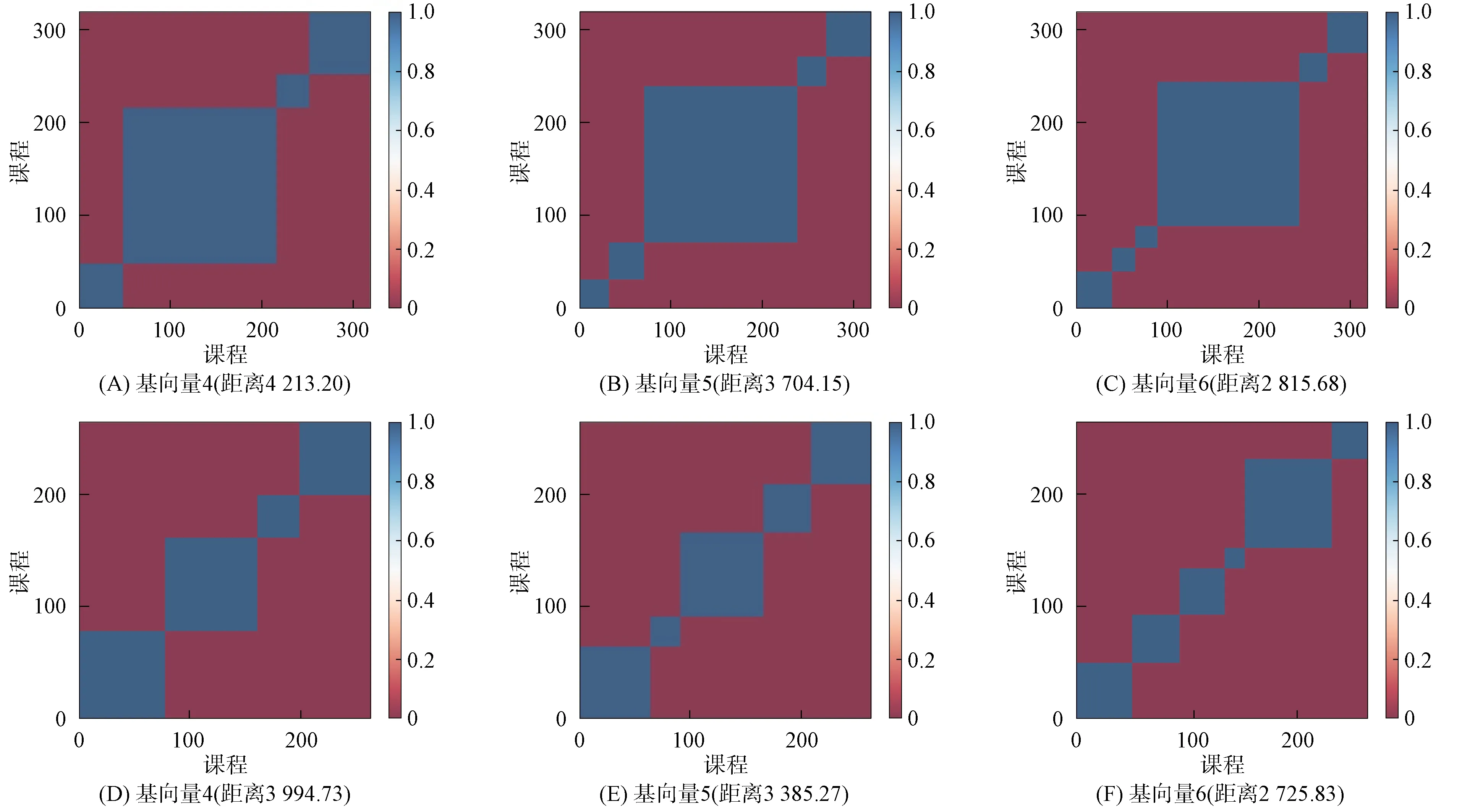
图3 基于自适应非负矩阵分解的学生和课程聚类分析结果

图3为自适应非负矩阵分解算法分解学生成绩矩阵的结果. 其中： 图3(A)～(C)为矩阵分解后课程层次聚类结果； 图3(D)～(F)为学生层次聚类结果. 当选择不同的基向量数目时, 聚类结果不同. 由图3可见, 实验分别选择了4,5,6共3组不同的基向量数目, 该参数直接影响聚类结果. 尽管课程分为基础课、 专业课和选修课, 但由图3(A)～(C)可见, 当基向量为6时, 重构矩阵误差ED=2 815.68为最低, 比基向量取4和5时分别降低了33.17%和31.55%. 结果表明, 对该学院开设的课程可进一步细分或用其他分类方法. 由图3(D)～(F)可见, 当基向量为6时, 重构矩阵误差ED=2 725.83为最低, 比基向量取4和5时分别降低了31.76%和24.1%. 该结果可为高校建设一流学科和优势特色专业、 优化专业设置提供数据支持. 虽然这些学生只来自4个专业, 但学生可根据自己的学习兴趣和职业规划不同划分更细致的学习社团, 如可将学生划分为6个学习社团. 要确定最佳基向量取值, 可将梯度下降自适应策略中的最大迭代次数变量用基向量替换, 从而得到面向基向量的自适应非负矩阵分解方法.

综上可见, 给定一个矩阵后, 当其他参数不变时, 最大迭代次数越大矩阵分解的结果越接近原矩阵. 但当达到某一阈值后, 矩阵分解的误差降低缓慢或不再降低. 同时, 随着迭代次数的增大, 算法的计算时间也快速增加. 本文提出了一种基于梯度下降自适应策略的非负矩阵分解算法, 该方法将自适应策略引入到矩阵分解求解过程中, 自适应地寻找NMF计算过程中的最大迭代次数并提高重构矩阵的精度, 使基于矩阵分解结构的聚类鲁棒性更强. 对吉林大学某学院学生成绩数据进行验证的实验结果表明, 基于梯度下降自适应策略的非负矩阵分解算法可明显提高矩阵分解的精度和鲁棒性, 该研究结果可为优化高校专业设置提供数据支持.