自主车辆高效多目标预测巡航控制

何德峰,崔靖龙,何文韬

(浙江工业大学 信息工程学院，浙江 杭州 310023)

车辆自适应巡航控制(ACC)是一种先进驾驶员辅助系统，它通过自动调节节气门开度或制动压力，实现车辆的定速巡航或跟车驾驶，减少驾驶员的负担并提高驾驶安全性[1-2]。模型预测控制(MPC)具有处理多变量多约束系统的优势[3-4]，在车辆ACC系统的应用越来越广泛，形成了相应的预测巡航控制(PCC)算法[5-7]。ACC系统存在多个相互冲突的性能指标[8-10]，如安全性、车辆跟踪性、驾驶舒适性以及经济性，满足了安全性和车辆跟踪性可能会造成驾驶舒适性和经济性的降低。为了解决这一问题，国内外学者进行了大量的研究并取得了一些研究成果。例如：文献[11]基于MPC提出一种最小化燃料消耗的最优控制算法；文献[12]采用有限时域下的动态规划，基于贝尔曼最优性原理和滚动策略，通过代价函数来计算ACC系统的最优反馈控制增益；文献[13]在MPC原理的基础上，提出一种多目标鲁棒前车跟驰的控制算法，充分考虑了前车加速度作为干扰变量的情况下，建立出车间距误差纵向动力学模型，所建立的模型能有效遵循车辆跟车的动态规划演变规律，大大提高了模型的精确度与巡航可靠性；文献[14]结合多目标协调的框架提出并采用实验验证了一种面向经济的车头时距控制算法，使得车辆同时兼顾跟踪能力和经济燃油性；文献[15]基于MPC综合了考虑安全性、舒适性、跟踪性能和经济燃油性多目标性能指标，并使用软化约束的做法求出多目标优化下的最优解。上述文章虽然实现了车辆ACC系统的多目标控制，但它们的在线计算量较大、实时性较低，同时随着车辆保有量的增加和日益复杂的交通环境，车辆ACC系统的多目标优化问题变得越来越复杂，需要解决优化目标快速实时求解的问题[16-17]。

为解决上述问题，笔者改进并提出了一种自主车辆高效多目标预测巡航控制算法。基于车辆ACC系统的多约束增量模型，釆用阶梯式控制策略[18]，将预测时域内的控制增量参数化成以阶梯形式变化，并利用MPC中的QP结构[19-20]，将变量进行适当的重新排序，接着使用原障碍内点法来解决优化问题，并引入Schur补以进一步减少计算负担。使用Matlab软件对新的算法在自适应巡航控制系统上进行仿真，得到相应的输出曲线，通过与传统模型预测控制的对比，验证了算法不仅满足了ACC系统的多个性能指标，同时显著降低了计算量，实现快速高效的预测巡航控制。

1 多目标ACC问题描述

ACC系统的控制器采用分层式控制结构，上位控制器通常用于收集车间距状态和驾驶员的输入信息，当前后车相对运动状态获得之后，如实时的车间距信息的获取，期望的车辆加速度就可以得以计算并作用到下位控制器；而下位控制器最重要的是节气门的开度，其变化是根据逆查询表所确定的，节气门的跟随控制与制动系统来相互配合，最终实现车辆以目标加速度运行，如图1所示。前车位置、速度和加速度分别表示为sp，vp，ap，本车位置、速度和加速度分别表示为sh，vh，ah。假设本车车辆配备有车载传感器以测量与前车的相对距离sr=sp-sh和相对速度vr=vp-vh，相对加速度ar=ap-ah通常是未知的，因为本车不能获得前车加速度ap，可以采用诸如卡尔曼滤波等方法来进行估计。

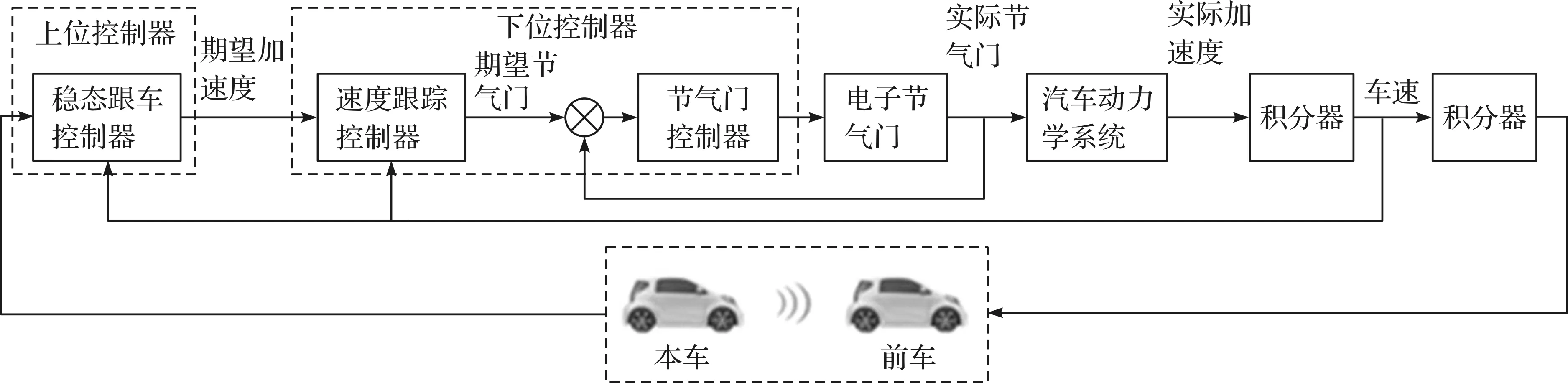
图1 提出的ACC系统的分层控制结构Fig.1 Hierarchical control structure of the proposed ACC system

在实际过程中，当指定的节气门开度和制动压力传输到车辆，车辆传动系统和制动系统的响应存在延迟时，采用一阶滞后系统来构建车辆的纵向动力学模型，即

(1)

式中：常数T1为执行器和传感器的一阶滞后；ah,c(t)为本车在时间t≥0的加速度指令。对于上层控制器，定义跟踪距离误差为e(t)=sr,s(t)-sr(t)，其中sr,s(t)是安全车间距。采用车头时距定义安全车间距为

sr,s(t)=T2vh(t)+sr,0

(2)

式中：sr,0>0为最小安全距离；T2>0为车头时距。在图1所示的ACC系统中，变量ah,c(t)将通过PCC算法实时计算。

为了应用PCC算法来计算ah,c(t)，可以通过采样时间Ts的零阶保持方式将式(1)的连续时间系统转换为离散时间系统，接着采用增量模型表示ACC系统的纵向动力学模型，即

(3)

由于车辆物理特性的限制以及跟车的安全性要求，要对ACC系统的控制变量和状态变量进行约束。定义控制输入和增量控制输入约束为

umin≤u(k)≤umax，Δumin≤Δu(k)≤Δumax

(4)

同时，状态变量x1(k)，x2(k)，x3(k)的约束分别为

-T2vh,max≤x1(k)≤0，vr,min≤x2(k)≤vr,max，ah,min≤x3(k)≤ah,max

(5)

式中：常数vr,min<0，vr,max>0；常数ah,min<0，ah,max>0且满足|ah,min|>|ah,max|。

车辆ACC系统存在多个控制目标，车辆跟踪性、安全性、驾驶舒适性以及燃油经济性，其中最基本的控制目标是在安全车间距离sr,s(t)内跟随前车。对此，引入代价函数来描述该ACC系统。就相对速度vr和跟踪距离误差e(k)而言，定义车辆跟踪性能指标为

(6)

式中we>0且wv>0。同时车辆的急促加减速会造成发动机在燃油方面不均匀的消耗，定义燃油经济性能指标为

(7)

式中权重wa>0且wac>0。进一步，为了抑制发动机转速的变化来提高驾驶员的纵向乘坐舒适性，应该减少控制输入的变化，即加加速度，定义车辆舒适性能指标为

J3(u(k))=wduΔu2(k)

(8)

式中wdu>0。最后使用这些权重将其作为单个代价求和，权重代表控制目标的相对重要性，则加权有限时域代价函数为

(9)

式中权重矩阵W(k)=diag{we(k),wv(k),wa(k),wac(k)}。

2 高效多目标预测巡航控制

2.1 阶梯式策略

笔者提出了阶梯式分段输入策略，即预测时域内的控制增量参数化为当前时刻控制增量的几何比例函数，其比率为β，则在预测时域[k,k+p]中的阶梯式控制量Δu(i|k)被规划为

Δu(i|k)=βΔu(i-1|k)i=1,2,…,p

(10)

进一步简化为

Δu(i|k)=βiΔu(0|k)i=1,2,…,p

(11)

式中：0<β<1为阶梯因子；Δu(i|k)为在k时刻对未来k+i时刻的预测值。

结合阶梯式控制输入式(11)，用ACC系统模型式(3)预测本车的未来状态为

(12)

式中：i=1，2，…，p。由于前车的未来加速度未知，因此使用其在过去时刻的估计值去近似未来的值，即d(k-1)=d(p-j|k),j=1，2，…，p。将式(12)转换为紧凑形式为

X(k+1)=Sxx(0|k)+SuΔu(0|k)+SyΔy(0|k)+Sdd(k-1)=Sxx(k)+SuΔu(0|k)+SyΔy(0|k)+Sdd(k-1)

(13)

式中x(0|k)=x(k)是当前时刻k的状态，相关矩阵为

(14)

此外，考虑到控制输入约束式(4)，利用阶梯式策略可得

(15)

进一步考虑状态约束式(5)，令Xmin=[-T2vh,max,vr,min,ah,min,umin]T，Xmax=[0,vr,max,ah,max,umin]T，可以得到

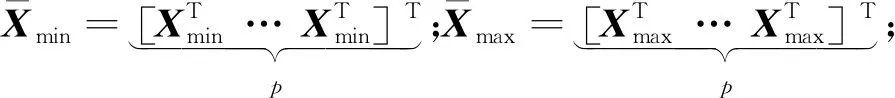
将式(11～13)代入代价函数式(9)，得到

(16)

(17)

式中x(k)为k时刻的状态。但不考虑系统约束，通过拉格朗日优化方法获得最优解，即

(18)

最优解可简化为

(19)

显然该最优解不能保证满足式(17)的约束。为此，可以使用二次规划求解工具来求解带约束的优化问题。通过式(19)的相应最优解来表示Δu*(k)。定义自主车辆预测巡航控制器为

uPCC(k)=u(k-1)+Δu*(k) ∀k=1,2,…

(20)

2.2 原障碍内点法

使用传统方法解决QP的速度很慢，限制了MPC在快速系统上的应用。对此，本节给出一种基于原始障碍内点法求解QP问题式(17)。

定义一个联合优化变量为

z=(Δu(k),x(k+1),x(k+2),…,x(k+p))

(21)

将QP问题式(17)以更简洁的形式重写为

minimizezTHzs.t.Pz≤h,Cz=b

(22)

式中：

再将QP问题式(22)中的不等式约束替换为目标中的障碍项，然后得到该近似问题为

minimizezTHz+κφ(z) s.t.Cz=b

(23)

式中：κ>0为障碍参数；φ(z)是与不等式约束相关联的对数障碍，定义为

(24)

2.3 不可行初始点的牛顿法

考虑不可行初始点的牛顿法解决问题式(19)。结合一个与等式约束Cz=b有关的对偶变量v∈RN。对优化问题式(23)求导后，得其最优条件即残差向量r=(rd,rp)为

rd=2Hz+κPTd+CTν=0rp=Cz-b=0

(25)

式中：di=1/(hi-piTz)；piT为矩阵P的第i行；κPTd为κφ(z)的梯度。将rp，rd分别称为原始对偶变量和残余变量，然后将问题式(23)的最优条件可以表示为r=0。

根据泰勒级数展开式，取前三项作为二次型函数，可将式(25)转化为

(26)

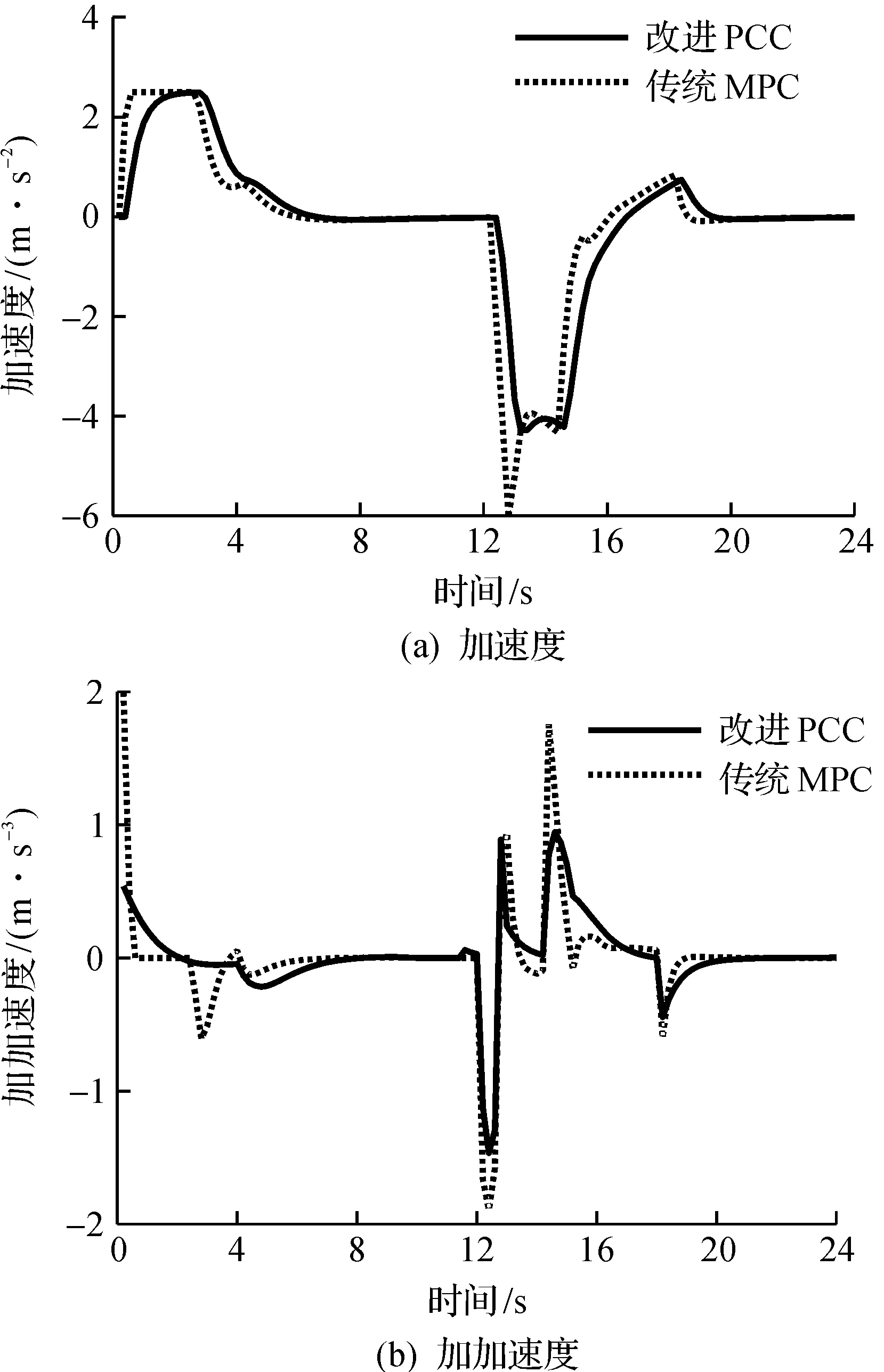
式中κPTdiag(d)2P为κφ(z)的Hessian阵，通过线性优化方程(26)计算出Δz和Δv，一旦Δz和Δv被确认，利用对残差r的范数形式的回溯直线搜索法获得s∈(0,1]，来保证迭代更新后的优化点满足不等式Pz

2.4 分块消元和Schur补

为了减少算法的计算量，通过分块消元求解线性方程式(26)的Δz和Δv。先定义块对角阵Φ=2H+κPTdiag(d)2P，接着执行以下步骤：

1) 形成Schur补集Y=-CΦ-1CT和ξ=-rp+CΦ-1rd。

2) 通过解决YΔv=-ξ来确定Δv。

3) 通过解决ΦΔz=-rd-CTΔv来确定Δz。

3 仿真与分析

在Matlab 2013平台上对提出的多目标预测巡航控制(PCC)算法进行仿真，并与传统MPC算法进行对比。仿真验证所使用的电脑CPU型号为Inter® Core(TM) i5-8300H 2.30 GHz，安装内存为8 GB，操作系统为Windows 10。仿真工况：前车与本车初始车速都为10 m/s，前车的车速变化规律为先加速后减速，最后稳定运行，主车由PCC算法控制跟踪前车。

ACC系统的参数选择为Ts=0.2 s，T1=0.5 s，T2=1.5 s，Sr,0=2 m，vmin=0 m/s，vmax=30 m/s，amin=-6.5 m/s2，amax=2.5 m/s2，umin=-5.5 m/s2，umax=2.5 m/s2，jmin=-2 m/s3，jmax=2 m/s3，we=1，wv=5，wa=1，wac=1，β=0.9。两种ACC算法获得的仿真结果展示在图2，3中，其中实线对应于PCC算法，虚线对应于传统MPC算法。

图2 车辆的速度和车间距变化曲线Fig.2 Velocity and inter-distance profiles of the vehicle

图3 车辆的加速度和加加速度变化曲线Fig.3 Acceleration and jerk profiles of the vehicle

从图2可以看出：两种算法可以满足跟踪能力的要求，追上了前车的速度，同时避免了车辆的碰撞，并且最终将间距调整到期望值。但使用改进PCC算法的车辆比使用传统MPC算法的速度响应更快，车间距变化更加平缓。以图2中的跟踪速度为例，在开始时，两种算法加速本车跟随前车，然后调节速度以适应前车的速度变化；在18 s以后，两种算法作用下本车的车速与前车的逐渐趋于一致，车间距也趋于安全值，这些结果符合现实驾驶员的跟车行为。

从图3中可以得出结论：传统MPC和改进PCC的本车加速度变化趋势大体相同。但是改进PCC下的本车，不仅峰值下降了28.79%，而且加速度变化更加平滑，因此从经济的角度上讲，改进PCC算法更具有经济性。另外，改进PCC算法显著降低了加速度的变化率即加加速度的峰值，降低了22.69%，曲线波动更加圆滑，可知与装配传统算法的车辆相比，驾驶员在装配改进PCC算法的车辆中会更加舒适。因此，所提出的算法在保证行车舒适性的同时还确保了行车安全和跟车性能。

最后，对比两种算法的单步优化平均计算时间，统计结果如表1所示。从表1中可以看出：当分别取预测时域p为5，10，15时，新的PCC算法的平均计算时间比传统模型预测控制方法分别降低了74.82%，73.66%，75.53%，显著减少了算法的计算时间。

表1 两种算法单步优化平均计算时间

4 结 论

面向ACC多目标优化控制问题，在阶梯式模型预测控制框架上，引入一种新的高效巡航控制算法。通过采用阶梯式策略，参数化预测时域内的控制输入变化量；同时利用MPC中QP问题的特殊结构，将变量进行适当重组，采用改进后的内点法来提高系统性能。在Matlab上验证了新算法的有效性，同时与传统MPC作了对比。实验表明：新的PCC算法不仅满足了ACC性能指标，即ACC系统的驾驶舒适性、经济性、安全性和车辆跟踪性，而且大大提高了算法的运行速度，体现出了高效性能，使其可以运用到更复杂的交通环境中。