竖向均布荷载作用下拱形蜂窝梁的挠度研究

袁伟斌，周蒸鑫，余 峰

(浙江工业大学 土木工程学院，浙江 杭州 310023)

拱形蜂窝梁的开孔形状有很多种，目前应用最广泛的是腹板开六边形孔和圆孔，相对于六边形孔，圆孔蜂窝梁的开孔在一定程度上减轻了截面开孔区域的应力集中问题。近年来，国内外学者对曲梁和蜂窝梁进行了大量的研究，Sapountzakis等[1]考虑了耦合扩展、弯曲、扭转、不均匀变形和剪切变形的影响，对曲梁进行了广义弯曲分析。Arici等[2]提出曲梁翼缘中线上的剪切变形是导致开口和闭口薄壁构件在不均匀扭转和截面畸变上理论差异的因素，并找到了解决该问题的方法。Tufekci等[3]分析了平面曲梁微分方程，考虑了轴向拉伸和剪切变形对曲梁稳定的影响，建立了有限曲面梁的有限元公式。Soltani等[4]用有限元模型分析了开孔形状分别为六边形和八边形的蜂窝梁的极限承载力。Daryan等[5]通过试验和有限元模型模拟分析了简支蜂窝梁的侧扭屈曲和腹板局部屈曲。Martin等[6]研究了正弦波孔蜂窝梁的承载力性能。郭彦林等[7]研究了两端固支钢拱平面外稳定的侧向支撑刚度阀值，用能量法推导得出钢拱平面外稳定的刚度阀值，并用有限元模型加以验证。吴晓等[8]根据弹性理论，提出了拉压弹性模量不同对曲梁的平面应力及位移的影响。王培军等[9]研究了不同开孔形式和腹板剪切变形对蜂窝梁屈曲性能的影响。赵滇生等[10]对蜂窝梁的强度和刚度进行了研究。袁伟斌等[11-13]从理论上研究了纯弯作用下蜂窝梁的侧向扭转屈曲，并提出了不同边界条件下的临界荷载解析解。

2019年4月为止，拱形蜂窝梁力学性能的研究分析十分稀少，针对上述拱形蜂窝梁研究存在的问题，提出了能量法，并考虑腹板剪切变形的影响，推导竖向均布荷载作用下拱形蜂窝梁跨中挠度的理论计算公式，并研究腹板开孔尺寸、构件曲率和构件长度对挠度的影响。其次使用有限元方法，利用ABAQUS对相应尺寸的拱形蜂窝梁进行了几何非线性分析，验证理论的准确性。

1 曲梁物理模型和基本公式

拱形曲梁几何尺寸如图1所示，坐标系为柱坐标系，O为坐标系的原点，x轴为柱坐标系的极轴，z轴为柱坐标系高度。设构件翼缘宽度和厚度为bf和tf，腹板高度和厚度为hw和tw，α1和α2分别为拱形曲梁右端和左端的极角，H、L和R分别为拱形曲梁截面形心轴的拱高、跨长和曲率半径，构件两端简支。q为竖向均布荷载值，e为曲梁截面中性层与形心轴的偏心距，θ和ρ分别为梁上任意点的极角和极径。根据卡氏第二定理，在拱顶施加单位力F，取竖直向上为正。对于一般的梁构件，其应变能主要由截面正应变和切应变分别产生的应变能组成，其中截面上的薄膜力与弯矩共同作用产生正应变和截面上的剪力作用产生切应变。

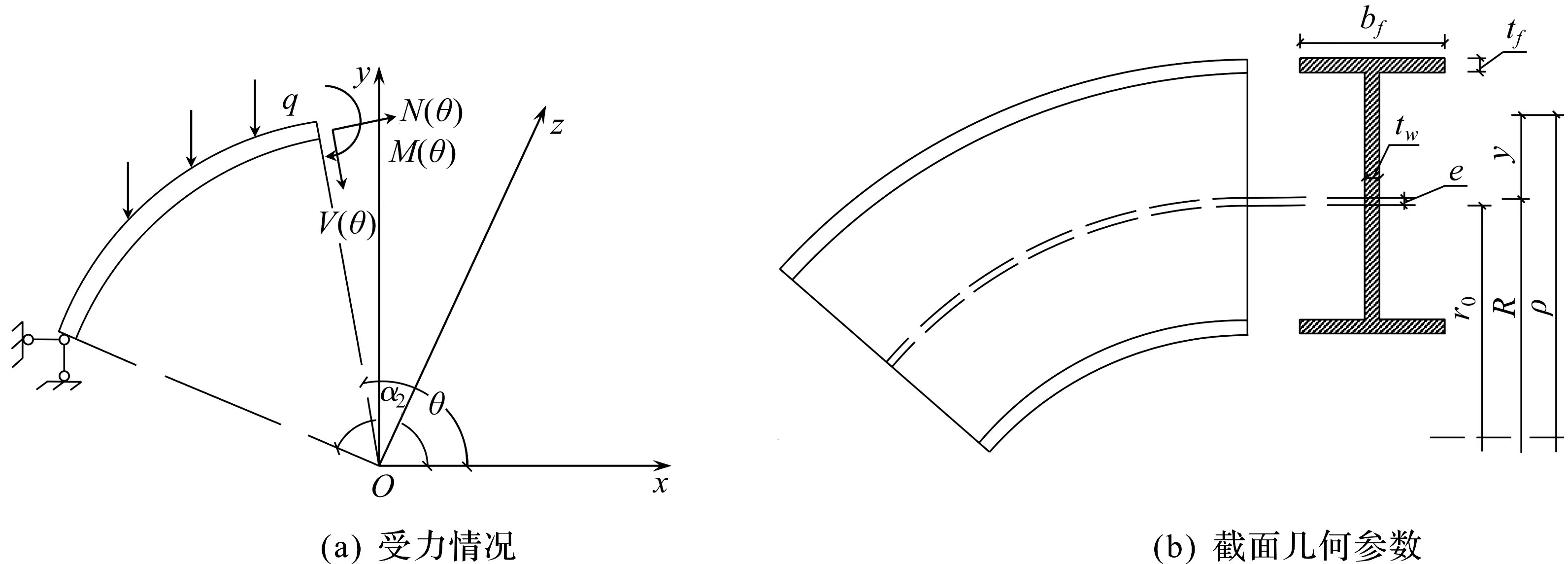
图1 拱形曲梁计算简图Fig.1 Calculation sketch of arched curved beams

构件任意截面上的平面内弯矩、轴力和剪力分别为

(1)

(2)

(3)

构件正应变能为构件上任意点正应变能密度的集合，即

(4)

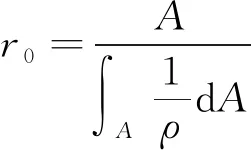
将式(4)中的弹性模量E和曲梁截面面积A提出，将体积积分转换为多重积分后，对ρ和z先积分并化简得到正应变能表达式为

(5)

为了更精确地计算拱形曲梁的挠度，将简化后的剪切应变能代入结构的总能量式中，再用能量法推导其挠度表达式，可以较精确地计算拱形曲梁的挠度。假设曲梁截面上切应力沿z轴方向均匀分布，根据切应力互等原理，从整体中取一微弧段，微弧段切割面上切应力大小相等，且微段两端正应力方向相反可以叠加计算。根据以上假设，宽度为b的曲梁微段切割面上的切应力与截面两端正应力的差值抵消能保持微段的受力平衡，则其平衡方程为

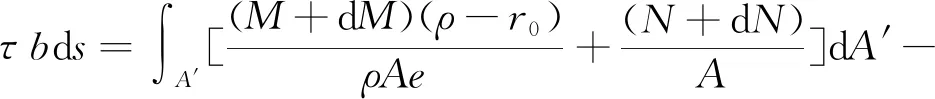
(6)

式中：τ为截面上的切应力，沿z轴方向均匀；b为曲梁微弧段宽度；A′为曲梁切割体的截面面积。因为研究的是浅曲梁，截面上不同极径的微弧段可以用截面形心轴的微段代替，即ds≈Rdθ。根据式(1～3)换算得到简支拱形曲梁在均布荷载作用下弯矩和轴力分别与剪力的对应关系为

(7)

(8)

取剪力与构件截面积的比值为截面平均切应力，并引入截面剪切放大系数，得到简化后的曲梁截面切应力表达式为

τ=αsτ0

(9)

(10)

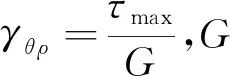
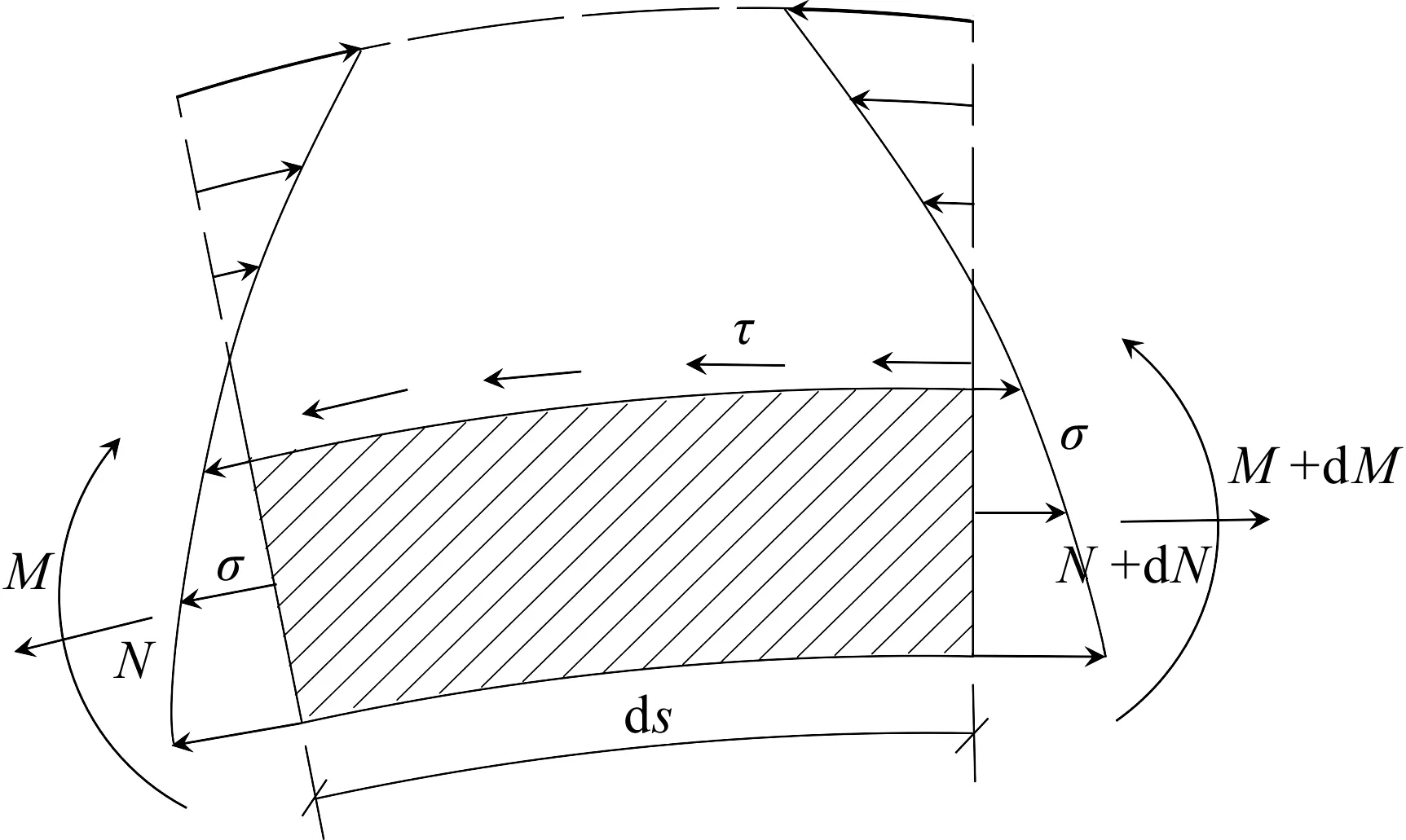
图2 曲梁微段受力简图Fig.2 The stress on curved beam micro-segment

微弧段长度取截面形心轴的曲率半径与曲梁微弧段的积，通过换算后得到曲梁截面剪切应变能表达式为

(11)

根据卡式第二定理计算曲梁跨中挠度，将假设的拱顶作用力F和均布荷载共同作用下的截面内力替换仅在竖向均布荷载作用下的构件内力，并将式(5，11)相加得到构件的总应变能为

(12)

(13)

设γ=α2-α1为曲梁所跨越的圆心角，先变分再分部积分得到等效刚度法计算的曲梁跨中挠度计算式为

(14)

2 拱形蜂窝梁跨中挠度的计算

圆孔拱形蜂窝梁尺寸如图3(a)所示，采用柱坐标系，右端和左端的极角分别为α1和α2，梁截面形心轴的拱高、跨长和曲率半径分别为H、L和R，构件两端简支。采用Timoshenko提出的等效抗弯刚度理论，将圆孔拱形蜂窝梁近似化处理，计算其等效惯性矩，以能量法推导的拱形曲梁跨中挠度计算公式为基础，根据费氏空腹桁架理论计算其跨中挠度的近似解。

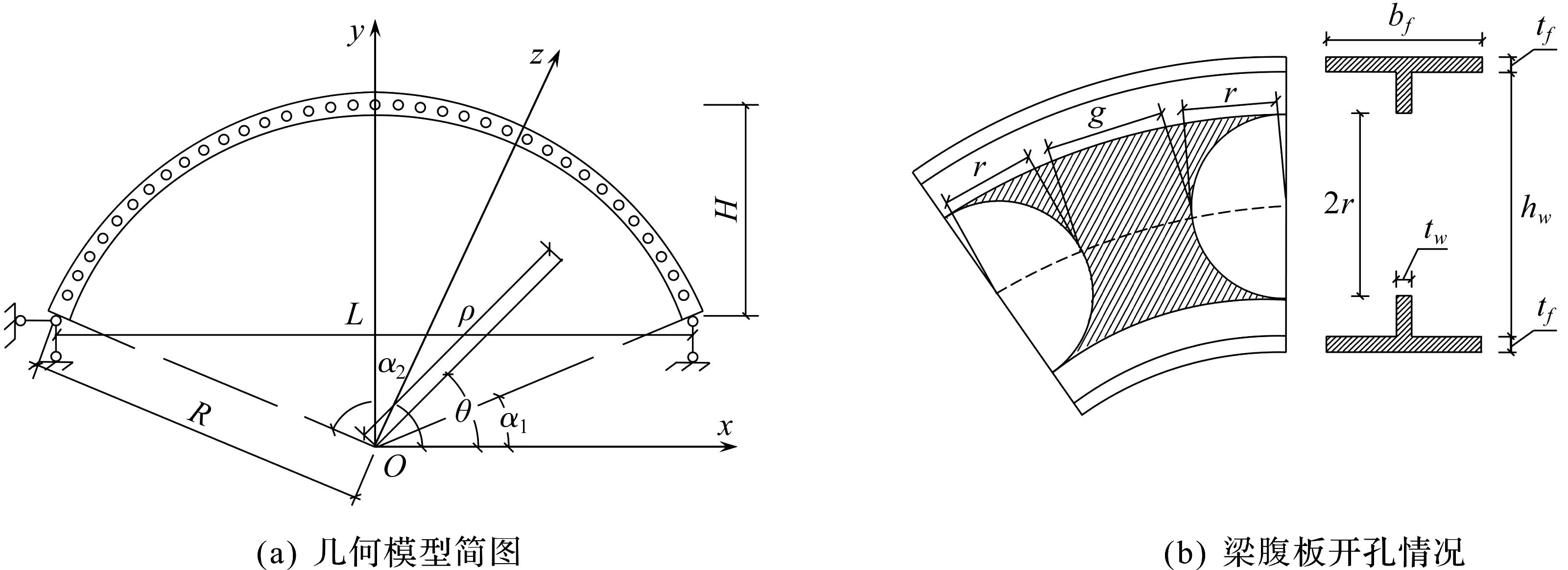
图3 几何参数简图Fig.3 Geometrical dimensions of arched castellated beam

圆孔拱形蜂窝梁腹板开孔如图3(b)所示，孔间距g和开孔半径r均取1/3hw，开孔的圆心在构件截面形心线上，其等效后的截面可看成由三部分组成的夹心梁，上翼缘和上部腹板连续的梁桥部分组成的T形截面和下翼缘与下部连续梁桥部分组成的T形截面可看作圆孔拱形蜂窝梁的“新翼缘”，腹板开洞部分截面可看成“新腹板”。“新翼缘”组成的空腹截面定义为空腹梁，其等效截面惯性矩根据I′=r0Ae计算为

Ik=rkAkek

(15)

式中：Ik为空腹梁截面的等效截面惯性矩；rk为空腹梁截面的中性层极径值；Ak为空腹梁的截面面积；ek为空腹梁截面中性层与形心轴偏心距。定义与拱形蜂窝梁相同尺寸，腹板不开孔的梁为实腹梁，同理可以求得实腹梁的等效截面惯性矩为

Is=rsAses

(16)

式中：Is为实腹梁截面的等效截面惯性矩；rs为实腹梁截面的中性层极径值；As为实腹梁的截面面积；es为实腹梁截面中性层与形心轴偏心距。图3为扇形孔单元梁段，其综合等效截面惯性矩可设为实腹梁和空腹梁沿弧长方向的均值，将g=r代入后，其综合等效惯性矩为

(17)

同理可以求得拱形蜂窝梁综合等效截面面积(图4)为

(18)

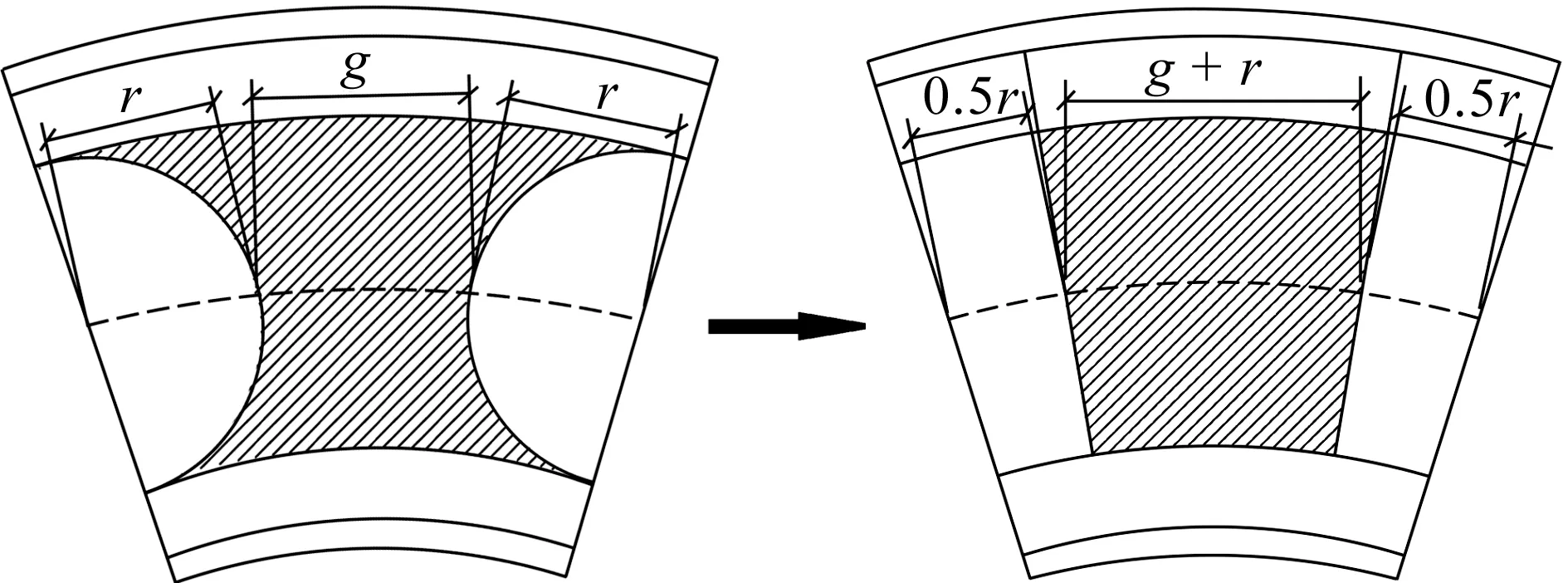
图4 腹板简化示意图Fig.4 Procedure of web simplify

由于圆孔拱形蜂窝梁与拱形曲梁所受荷载条件和边界条件相同，两者的内力分布也相同。圆孔拱形蜂窝梁的综合等效惯性矩和综合等效截面面积分别代替拱形曲梁等效惯性矩和截面面积，代入式(14)，得到竖向均布荷载作用下，圆孔简支拱形蜂窝梁的跨中挠度计算式为

(19)

3 有限元分析

对拱形蜂窝梁有限元分析中，利用壳扫掠的方法建立模型，采用壳单元进行弹性分析，材料的属性统一采用如下定义：弹性模量E=210 GPa，泊松比v=0.3，壳体材质均匀且为各项同性的弹性材料。拱形蜂窝梁模型为平面外简支，左右端截面z轴方向位移设置为零，左端截面中心x，y轴位移为零；右端截面中心y轴位移为零，且上翼缘施加竖直向下的均布面荷载。采用10 mm×10 mm的网格尺寸，曲率控制的最大偏离因子为0.01。拱形蜂窝梁模型截面如表1所示。表1中：翼缘宽度为bf；翼缘厚度为tf；腹板高度为hw；腹板厚度为tw；蜂窝梁形心轴的曲率半径为R；构件跨长为L；荷载为q。构件模型详见图5。

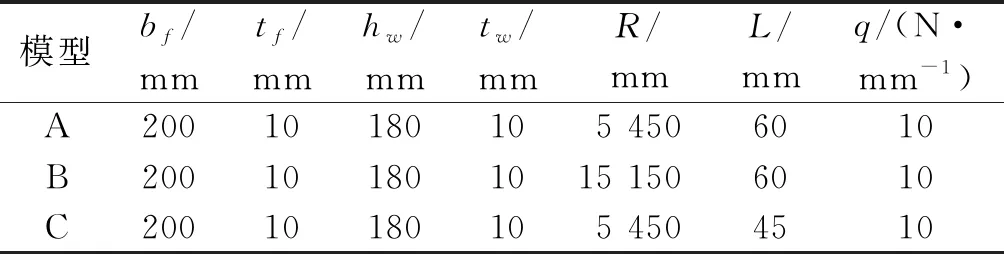
表1 拱形蜂窝梁截面参数表Table 1 Section parameters of arched castellated beams

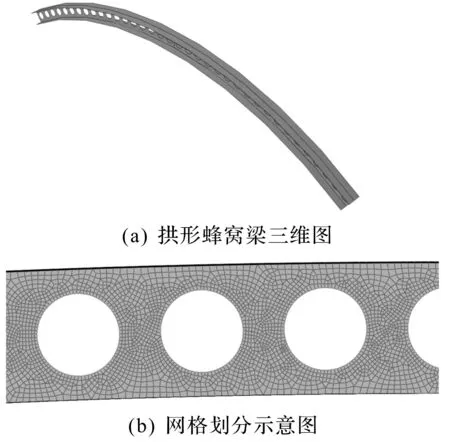
图5 有限元模型图Fig.5 Finite element models

通过截面B、C与截面A的结果对比，在构件跨长和挠度关系图(图6～8)中：对于相同截面和曲率的构件，其跨中挠度的有限元解和理论解均随跨长呈非线性增长趋势；对于开孔为2/3腹板高度的构件，其理论解与有限元解比值随跨长增大而增大，且小于1；对于腹板开孔为1/2腹板高度的构件，其比值随跨长增大而减小，且始终处于1.07～0.97。由图6～8还可知：曲率小，其理论解与有限元解的比值小，准确性好；当构件单元数较少时，开孔构件理论解相对于有限元解偏小且误差较大，是因为在截面和曲率不变的情况下，构件长度越短，其跨高比越大，截面剪切变形的影响也随之增大，笔者理论计算过程中，剪切应变能近似化计算过程的误差可能会在这种情况下被放大，且在计算构件应变能时，对构件腹板孔洞进行了简化，简化后得到的综合等效截面惯性矩和截面面积不能完全反应原始构件的相应力学性能。

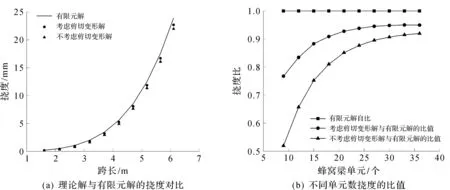
图6 拱形蜂窝梁跨长与挠度关系图(模型A)Fig.6 Relationship between length and deflection(model A)

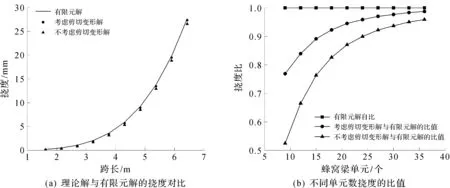
图7 拱形蜂窝梁跨长与挠度关系图(模型B)Fig.7 Relationship between length and deflection(model B)

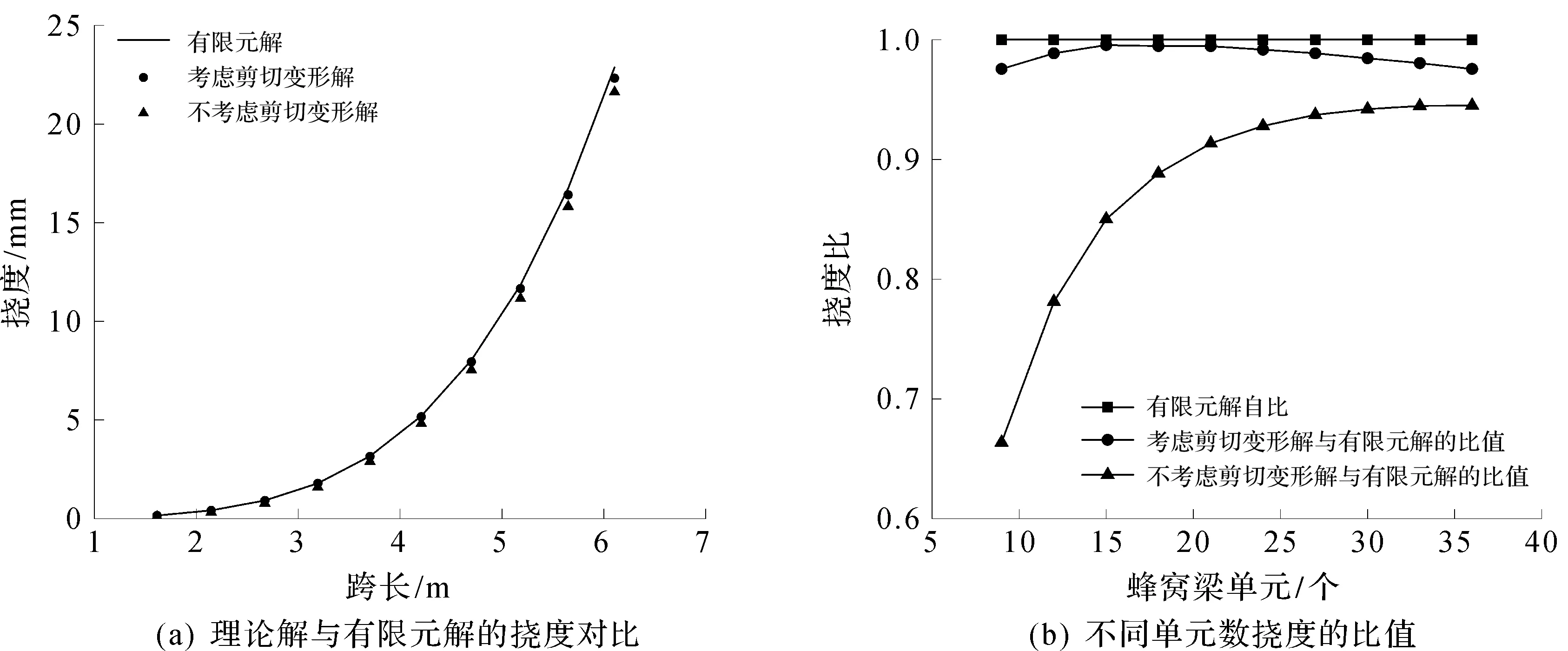
图8 拱形蜂窝梁跨长与挠度关系图(模型C)Fig.8 Relationship between length and deflection(model C)

4 结 论

利用能量法求解的简支拱形曲梁和简支圆孔拱形蜂窝梁跨中挠度的计算公式准确性较好，能够作为简化挠度计算或验证简化计算公式的依据。蜂窝梁跨中挠度考虑剪切变形时的理论解数值较不考虑剪切变形的约大30%；腹板开孔尺寸对挠度计算公式的准确度有一定影响，尤其在高跨比较大时，小开孔组的笔者理论解最大值比大开孔组大约20%；曲率对笔者理论解的影响较小且不超过4%。理论计算中的假设与实际情况存在一定的差异，因此挠度的推导公式存在一定的误差，通过等效刚度法和增加剪切能量项的方法，利用截面剪切变形对圆孔拱形蜂窝梁跨中挠度的影响，可以有效地提高挠度推导公式的准确性，使挠度值与有限元分析的结果比较吻合。