一类非线性微分方程三阶三点边值问题正解的存在性
2020-07-16郭丽君
淮阴师范学院学报(自然科学版) 2020年2期
郭丽君
(兰州交通大学 博文学院电信工程系,甘肃 兰州 730101)
0 引言
非线性微分方程在各种不同领域都有着很重要的应用,因此,一直以来非线性微分方程正解的存在性研究有着不可动摇的理论价值和深刻的应用背景,已经有很多研究者对非线性微分方程边值问题正解的存在性进行了探讨,并得到了很多好的结论和成果[1-9].但在大多数成果中,为了得到正解的存在性理论都对微分方程的非线性项作了特别限定和要求,使得理论成果在应用时有一定的局限性.在文[7]中,作者研究了如下三阶三点边值问题

本文考虑三阶三点边值问题
(1)

1 预备引理


其中
引理2[1]对任意(t,s)∈[0,1]×[0,1]有0≤G(t,s)≤1-s.
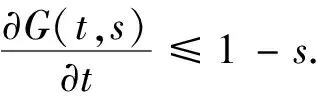
证明对格林函数G(t,s)关于变量t求导,可得
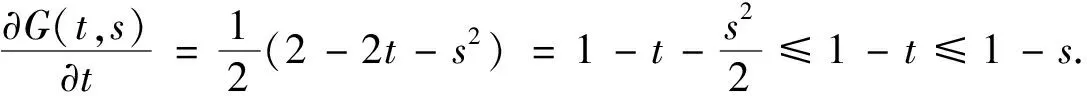
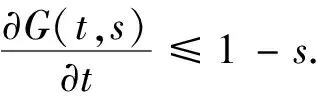
因此,引理得证.
引理4(Schauder不动点定理)[10]设E是Banach空间,B⊂E是E中的有界闭凸子集假设T:E→E是全连续算子且T(B)⊆B.那么T在B中至少有一个不动点.
2 主要结果
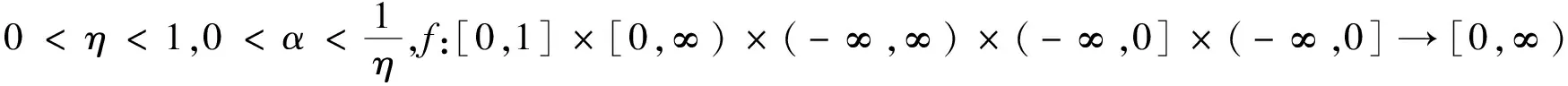
那么边值问题(1)至少存在一个正解
证明设Banach空间E=C[0,1],对u∈E,定义算子

显然A:E→E是全连续的,且A的不动点即为边值问题(1)的解.令
下面只需寻找A在B中的不动点.对任意u(t)∈B,t∈[0,1],首先由引理2及已知条件可得

(2)
其次对算子A求一阶导数,由引理3及已知条件可得
(3)
另一方面


(4)
接着对算子A求二阶导数可得

显然有
(5)
最后,对算子A求三阶导数可得
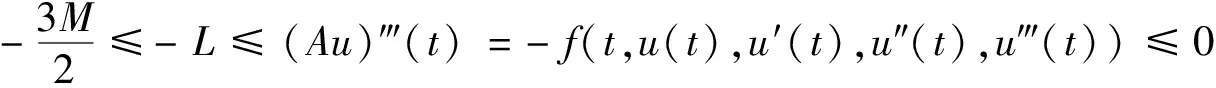
(6)
由式(2)和式(6)可知A(u)∈B,即A(B)⊆B根据引理4可知,算子A至少有一个不动点u*∈B,即为边值问题(1)的正解.
