江浙沪地区降雨极值的半参数拟合

徐鹏程

(南京财经大学 应用数学学院, 江苏 南京 210046)

0 引言

近年来,极端气候事件出现的频率和强度均有所增加,造成了严重的经济损失和人员伤亡,引起了人们广泛的关注.我国是一个洪涝灾害频发的国家.研究显示：过去半个世纪以来,我国越来越多的地区降水有集中趋势[1].气候要素是一个随机变量,极值就是这些随机的变量的某种函数,研究气候变化可以从研究极值入手,利用统计极值理论方法研究降水,特别是极端降水变化规律,对洪水风险评估、区域防灾减灾、防洪设施工程设计等具有重要意义和参考价值.

极值理论和分布拟合方法广泛被运用于分析降雨、洪水等极值数据的分布规律等研究.目前研究极端降水的统计分布模型有对数正态分布、广义极值分布(GEV)、威布尔(Weibull)分布、耿贝尔(Gumbel)分布、Gamma分布、广义帕累托分布(GPD)、皮尔逊Ⅲ(Pearson-Ⅲ)分布等.如赵立将GEV和Gumbel分布应用于拟合五华县降水极值[2];王文琪等人利用GEV和GPD分布研究太湖流域湖西浙西区降水极值特性[3];杜晓阳等人用皮尔逊Ⅲ、对数正态、指数、耿贝尔等概率分布拟合分析广州市单日降水量的极值特征[4];张玉虎等人探讨了不同的分布函数对不同降雨极值序列的适用性[5];张延伟等人选用GEV和Gumbel分布研究新疆地区降水概率分布特征[6];李亚丽使用Gumbel分布拟合陕西短历时降水百年极值[7];张萍应用广义极值分布、正态分布和Gamma分布拟合珠江流域极端降水[8]; 王红利用Weibull分布拟合广西一日最大降水量的概率分布[9].此外,还有很多学者对各地降雨的时空变化特征进行了研究.自从Qin和Zhang建立半参数模型以来,半参数密度比模型就成为现代统计的研究热点[10].例如,Folkianos建立了半参数的密度估计方法[11].Qin给出了来自不同样本分布的混合比例的半参数统计推断[12].Zhang利用最大似然方法[13],研究了半参数的分位数估计方法.

不同的站点数据通常需要用不同的概率分布进行拟合[14],从而寻找到该站点的最优拟合分布模型,而选择多种概率分布函数不便于分析降雨极值的分布规律.为了用同一类分布函数拟合分析不同的站点,本文由经典logistic回归模型构造出一个多样本半参数概率密度比模型,将此模型用在降雨极值拟合上研究和分析长序列降雨极值.

1 多样本概率密度比模型及其参数估计

1.1 k样本logistic模型

k样本概率密度比模型可以由经典logistic回归模型导出.设X11,X12,…,X1n1是来自第1个总体的样本,Xk1,Xk2,…,Xknk是来自第k个总体的样本;k组样本相互独立令D=i代表第i个总体,i=1,2,…,k,对给定的测试数据X=x,多样本的logistic回归模型是:

(1)

1.2 k样本概率密度比模型的密度函数

类似于Qin等的处理[10],由贝叶斯法则得到模型(1)等价于如下的半参数密度比模型:

Xk1,Xk2,…,Xknk～gk(x)

(2)

1.3 k样本概率密度比模型的参数估计

首先引入一些记号,令{T1,T2,…,Tn}代表合并的样本{X11,…,X1n1,X21,…,X2n2,…,Xk1,…,Xknk},且令n=n1+n2+…+nk.参数估计的方法采用Owen提出的经验似然方法[16]进行,样本的经验似然函数为:

记Pi=dGk(Ti),这里,Pi可以理解成概率分布在每个观测值上赋予的概率,即Pi是概率的跃变且总和为1,故

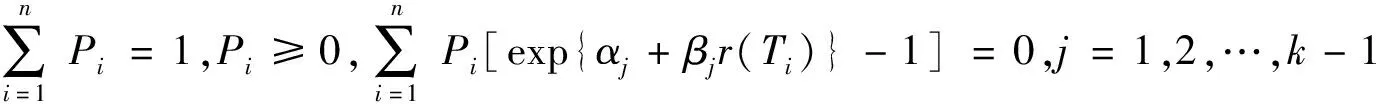
其计算由R语言[17]实现,这里j=1,2,…,k-1,l(αj,βj)是关于(αj,βj)的剖面对数似然函数:

1.4 k样本概率密度比模型的分布函数

1.5 分布拟合的Kolmogorov-Smirnov距离

K-S检验的检验方法是将样本数据的累计频数分布与特定理论分布比较,如果两者的K-S距离很小,可推断理论分布和经验分布拟合很好.设y1,y2,…,yn是样本量为n的样本且已按升序进行了排序,K-S检验的原假设H1:经验分布的累计频率来自于理论分布;备择假设H2:经验分布的累计频率不是来自于理论分布.用F(x)和Fn(x)分别表示理论分布和经验分布的累积频率,原假设H1为真时,K-S检验统计量定义为D=maxx∈R|Fn(x)-F(x)|.K-S距离表达式为:

(3)

其计算由R语言实现.

2 降雨极值数据的半参数密度比模型拟合

2.1 数据来源

降雨极值数据来自中国气象科学数据共享服务网提供的逐年日降雨极大值资料(单位:1 mm),时间为1951-2018年(站点的起始时间不完全一致),范围为江浙沪地区10个气象站点气象站点包括徐州、赣榆、南京、东台、宝山、徐家汇、杭州、定海、温州、瑞安等,以上站点序号依次为1-10.样本量最大为68,最小为59.

2.2 半参数密度比模型对降雨极值的参数拟合

选用极大似然估计方法进行参数的拟合.第一步选择r(x)=(x,x2)T,求出样本的经验似然,根据拉格朗日乘子法,解计分方程组得出参数.第二步将由R语言计算所得的参数代入,从而得到拟合半参数概率密度比模型的分布函数.第三步将拟合半参数概率密度比模型的分布函数与样本累积频率进行比较,由软件可绘制出拟合图，图1给出了部分站点半参数密度比模型的分布函数与样本累积频率.由图中可以直接看出半参数概率密度比模型的分布函数和样本累积频率接近,拟合效果较好.

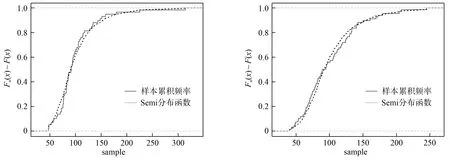
(a)站点1 (b)站点3

(c)站点6 (d)站点9

2.3 与其他分布法的K-S距离比较

广义极值分布(GEV)多用于模拟历史降水和径流,估算不同重现期最大值;Gumbel分布被广泛应用于单站频率计算和特征值分布规律模拟中;Gamma分布是气候统计学中重要的偏态分布,能够稳定的描述降水量的分布;Weibull分布则广泛应用于对各种极值数据的拟合.当得到半参数概率密度比模型的分布函数后,由式(3)分别计算半参数概率密度比模型(以下简称Semi分布)与拟合GEV、Gumbel分布、Gamma分布、Weibull分布的K-S距离,如表1所示.

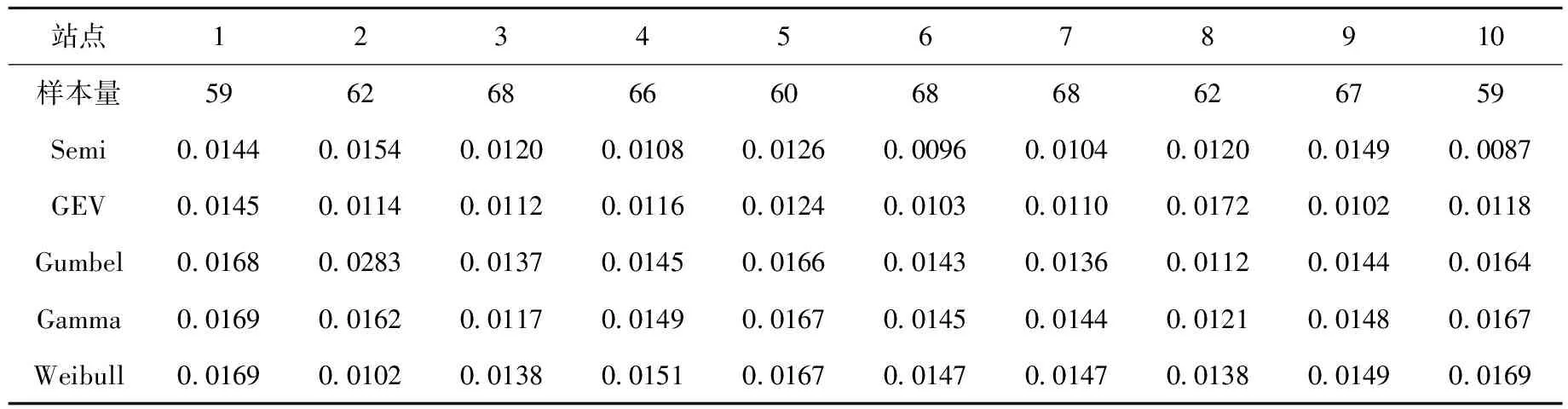
表1 Semi、GEV、Gumbel、Gamma、Weibull分布法的K-S距离

比较上述5种分布的K-S距离折线图,如图2所示.可以观察到Gumbel分布、Gamma分布以及Weibull分布的K-S距离明显大于Semi分布和GEV分布的K-S距离.可以看出Semi分布和GEV分布更适合所有站点的数据拟合，再将Semi分布的K-S距离和GEV的K-S距离进行比较,观察到10个站点中,有6个站点的Semi分布的K-S距离小于GEV的K-S距离.一般来说,Semi分布略优于GEV分布.

用5表示最大距离,4次之,以此类推,1表示最小,这样得到10个站点各分布的最小距离次序,如表2所示.比较上述5种分布的K-S距离次序,Semi分布有5次最小,GEV分布3次,Gumbel分布和Weibull分布各1次.Semi分布的K-S距离次序的平均数和方差分别为1.90和1.21,而GEV分布的K-S距离次序的平均数和方差分别为2.00和1.33,均高于Semi分布,这表明Semi分布比GEV分布更加稳定.

表2 5种分布法的K-S距离排序

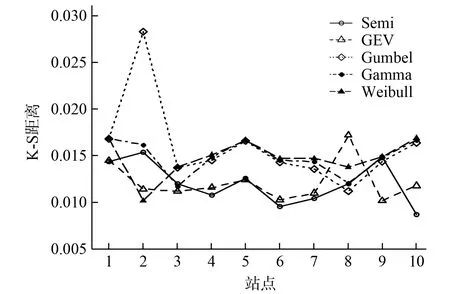
图2 5种分布法的K-S距离折线图

3 结论

由经典Logistic回归模型导出多样本半参数概率密度比模型,采用极大似然方法估计多样本半参数概率密度比模型的参数,并拟合逐年日降雨量序列,利用R语言计算K-S距离,并与其他4种常见的用于拟合降雨量极值数据的分布比较,得出以下初步结论:

1)半参数概率密度比模型的分布与广义极值分布、Gumbel分布、Gamma分布、Weibull分布拟合优度度量表明：半参数概率密度比模型的分布与广义极值分布对大部分站点拟合的K-S距离总体偏小,而Gumbel分布、Gamma分布和Weibull分布对于部分站点拟合的K-S距离偏大;半参数概率密度比模型的分布与广义极值分布比较,半参数概率密度比模型的分布的K-S距离更小也更稳定.所以半参数概率密度比模型可以适应不同站点的降雨极值提高拟合的稳定性.

2)半参数概率密度比模型能更好的模拟降雨极值的概率分布,通过选取适合的r(x)可以提高拟合准确率,有助于分析降雨极值的分布规律,是研究气候变化下极值事件统计特征的重要工具,为估算降雨极值的重现期提供了有效方法.