确定Tikhonov参数的改进函数法

2020-07-16胡宇清王兵贤

淮阴师范学院学报（自然科学版） 2020年2期

胡宇清, 王兵贤

(1.金陵科技学院理学院，江苏南京 211169；2.淮阴师范学院数学与统计学院，江苏淮安 223300)

0 引言

偏微分方程反问题一直是应用数学和计算数学领域的研究热点，它广泛存在于自然科学和社会科学中，是地球物理勘探、油气油田开发、材料的无损伤检测、人体癌症肿瘤的检测、雷达和声纳的探测与跟踪等应用科学的基础[1-8].当我们把具体的物理现象用微分方程定解问题来描述时，反问题一般是重构微分方程中的未知系数、边界形状、边界系数、边界条件或初始条件.从数学理论的角度看，此类问题的研究难点在于其不适定性和非线性性.当我们利用的输入数据是有扰动的测量数据时，在经典意义下问题的解可能不存在，解即使存在也可能不唯一，且可能不连续依赖于输入数据，即输入数据小的观测误差会导致近似解与真解的严重偏离.众所周知，处理这类问题最基本的工具是正则化方法.Kunisch[9]提出了基于吸收的Morozov偏差原理，用模型函数的方法求解了Tikhonov正则化参数；在文献[10-13]中，作者对模型函数法加以改进，得到了基于吸收Morozov偏差原理全局收敛的模型函数算法.

本文由Tikhonov正则化方法提出的拟解概念，构造拟解方程，在传统的模型函数下引入3种含待定参数且具有明确表达式的函数来构造拟解方程的逼近形式，从而迭代求解得拟解方程的近似零点.在迭代过程中，模型函数的待定参数不断更新，得到了算法具有全局收敛性.

1 问题的提出

反问题往往是不适定的，这是由于观测数据一般情况下会有误差，在确定未知解或者参数时观测数据的微小误差常常会引起解的急剧变化.为了获得稳定的数值解，在求解反问题时应使用正则化技巧，这就涉及到正则化参数的有效选取.反问题通常归结为第一类算子方程的形式：

Kx=y

(1)

其中K是从希尔伯特空间X到Y的线性紧算子.在实际应用中，输入数据y经常会产生微小误差，记yδ为y的误差水平为δ的扰动数据，因此在误差数据yδ满足‖yδ-y‖Yδ的条件下，考虑算子方程(1)的等价形式:

Kxδ=yδ

(2)

解形如算子方程(1)的线性不适定反问题，常用的方法是Tikhonov正则化，其基本思想为求泛函:

(3)

在正则化过程中，正则化参数的有效选取一直是不适定问题研究中的一个重要课题.常用的两种正则化参数α的选取策略为：

1)先验选取法：根据精确解的光滑性等信息取得，这实际是很难预先给出的；

2)后验选取法：基于误差数据和误差水平取得，此方法更为实用.基于后验选取策略，目前有很多较成熟的方法：Morozov偏差原理[1,14]，L-曲线法[15-16]等.

本文在Tikhonov正则化下，基于拟解方程，对传统模型函数法加以改进，研究了3种改进的迭代模型函数法，其中包含了单参数和双参数模型.首先由Tikhonov正则化的相关结论给出拟解方程.

2 拟解方程

引理1[1-2]设K是从希尔伯特空间X到Y的有界线性紧算子，则Jα(x)存在唯一的极小元xα(δ),δ，且xα(δ),δ为方程

αxα(δ),δ+K*Kxα(δ),δ=K*yδ

(4)

的唯一解.方程(4)中的解可以写作xα(δ),δ=Rαy，其中Rα:=(αI+K*K)-1K*，且有如下结论：

1)‖Rα‖

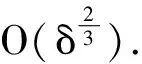
引理2[1,2]设y∈Y,α>0, 且xα(δ),δ是方程αxα(δ),δ+K*Kxα(δ),δ=K*yδ的唯一解，则有如下结论：

1)xα(δ),δ连续地依赖于α,y；

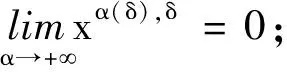
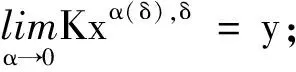
4)若K*y≠0，则映射α→‖xα(δ),δ‖X为严格单调减，映射α→‖Kxα(δ),δ-y‖Y为严格单调增.

从优化理论角度看，Tikhonov正则化方法可以看成带约束的两个优化问题：

问题1 假设δ>0，在约束条件‖Kx-yδ‖δ下求‖x‖的极小值(偏差原理).

问题2 假设ρ>0，在约束条件‖x‖ρ下求‖Kx-yδ‖的极小值[17].

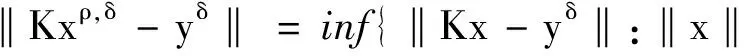
定理1[2]假设K为从希尔伯特空间X到Y有界的一一的线性算子，K(X)在Y中稠密，在ρ>0下，∀y∈Y, 方程(1)有唯一的具有模约束ρ的拟解.

问题2的正则性假设K为从希尔伯特空间X到Y的有界的一一的线性算子，K(X)在Y中稠密，对y∈K(X)，yδ满足‖yδ-y‖δ，则

1)若ρ≥‖K-1y‖，当δ→0时有xδ弱收敛至K-1y；

2)若ρ=‖K-1y‖，则当δ→0时有xδ收敛至K-1y.

(5)

这是一个关于正则化参数α的非线性方程.确定正则化参数的困难在于如何高效求解方程(5).文[2]中，作者用牛顿迭代法求解了拟解方程(5)，但迭代初值α的选取有限制条件αρ‖K‖δ，这在实际应用中往往很难做到，且只有局部收敛性.在文[10][11]中，作者提出了用模型函数法求解偏差方程，并得到了全局收敛性，故本文在拟解方程(5)的基础上改进传统的模型函数，进而用迭代法求解正则化参数.

F(α)和x(α)都是关于α的无穷次可微函数，x(α)和x′(α)分别满足如下两个等式：

αx(α)+K*Kx(α)=K*yδ.

αx′(α)+K*Kx′(α)=-x(α).

对任意的α>0，通过计算可得：

当且仅当yδ∈kerK*时，x(α)=0，因此在下面的讨论中都假设yδ∉kerK*，从而由x(α)≠0，得x′(α)≠0，最终推得：F′(α)>0，F″(α)<0.

根据F(α)的定义，可得：

2F(α)+2αF′(α)+‖Kx(α)‖2=‖yδ‖2

(6)

由F′(α)的表达式，拟解方程(5)可改写为：

(7)

从而N′(α)=F′′(α)<0.由F(α)的性质，可得拟解方程(7)一定有解.

定理2 假设K为从希尔伯特空间X到Y的有界唯一的线性算子，K(X)在Y中稠密，则N(α)一定有唯一的零点.

3 基于拟解方程的迭代算法

虽然F(α)有较好的性质，但其具体形式未知，所以直接求解拟解方程(7)的数值实现较难，计算量较大，故考虑用模型函数法求解.引进函数F(α)的具有明确表达式的且含有待定参数的近似函数m(α)，进而拟解方程(7)可以近似为：

(8)

通过不断更新模型函数m(α)中的待定参数使其更好地逼近无明确表达式的函数F(α)，从而由方程(8)可得求解拟解方程的迭代算法.这里的模型函数m(α)是通过近似函数F(α)满足的精确方程得到的, 且在不同的近似意义下可得不同的模型函数.

3.1 传统的模型函数法

因为‖Kx(α)‖2与函数F(α)的关系未知，故Potter考虑的传统模型函数[8]是将式(6)中的‖Kx(α)‖2局部近似于T‖x(α)‖2=2TF′(α)，其中T为常数.记F(α)的模型函数为m1(α)，将F(α)的模型函数m1(α)代入式(6)得：

解出该微分方程：

其中C和T为需要迭代得到的两个常数，m1(α)给出了函数F(α)的解析表达式，从而新的正则化参数的近似值由拟解的近似方程(8)得到.

算法1 1)给定初始值k=0,拟解的近似方程(8)的零点α0,迭代误差ε>0和模约束ρ；

2)解正则化方程(4)得到x(αk)，并计算F(αk)，F′(αk)；

6)当|αk+1-αk|ε时迭代停止，否则令k:=k+1，返回第1步.

模型函数法的几何解释，如图1.

图1 传统模型函数法的几何解释

α*为拟解方程的精确解，通过逐次迭代，拟解的近似方程的零点离α*越来越接近.

定理3 若Nk(αk)<0且αk充分小，则拟解的近似方程N(α)=0有唯一解.

这种方法的收敛性是局部的，因此改进此方法得全局收敛性.下面3种方法均为改进的迭代函数法.

3.2 改进的单参数模型函数法

其中C和T为需要迭代得到的两个常数，则m2(α)为函数F(α)的另一种解析表达式，从而新的正则化参数的近似值由拟解的近似方程(8)得到.

算法2 1)给定初始值k=0,拟解近似方程(8)的近似零点α0,迭代误差ε>0和模约束ρ；

2)解正则化方程(4)得到x(αk)，并计算F(αk)，F′(αk)；

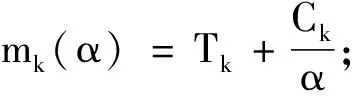
6)当|αk+1-αk|ε时迭代停止，否则令k:=k+1，返回第1步.

该算法的第5步加入了二分法，类似文[10]中的结论，可直接得到该算法的全局收敛性：

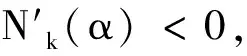
3.3 两种改进的双参数模型函数法

基于F(α)的表达式及拟解方程(7)，提出更广泛的模型函数法，含两个参数的模型函数法.

算法3 1)给定初始值k=0,拟解近似方程(8)的近似零点α0,迭代误差ε>0和模约束ρ；

2)解正则化方程(4)得到x(αk)，并计算F(αk)，F′(αk)；

4)得到第k步的模型函数mk(α):=m(α;Ck,Tk)；

6)当|αk+1-αk|ε时迭代停止，否则令k:=k+1，返回第1步.

与算法2相同，该算法的第5步加入了二分法，同样可直接得到该算法的全局收敛性：

定理5 若初始值α0∈(α*,1)，则由算法3产生的序列{αk}是单调减的，且收敛到精确的正则化参数，也就是拟解方程的解.

下面这种双参数的模型函数法是基于拟解函数N(α)定义的.

算法4 1)给定初始值k=0,拟解近似方程(8)的近似零点α0,迭代误差ε>0和模约束ρ；

2)解正则化方程(4)得到x(αk)，并计算F(αk)，F′(αk)；

4)得到第k步的模型函数Nk(α):=n(α;Ck,Tk)；

6)当|αk+1-αk|ε时迭代停止，否则令k:=k+1，返回第1步.

该算法的第5步加入了二分法，同以上算法类似可直接得到算法4的全局收敛性：

定理6 若初始值α0∈(α*,1)，则由算法4产生的序列{αk}是单调减的，且收敛到精确的正则化参数，也就是拟解方程的解.

改进的3种算法是将二分法嵌入到迭代算法中，而非直接利用二分法，使得算法不会在有限步停止，从而使得序列{αk}是无穷的且精确收敛到拟解方程的唯一解.算法2单纯从拟解方程出发，构造模型，较狭隘；算法3和算法4的应用范围更广；相对于算法3而言, 算法4的模型函数方法不仅对普通的模型函数适用, 而且能够得到更为有效的迭代算法.本文提出的3种改进算法的运算速率有所差别，算法4的迭代所需时间最短，即迭代次数最少，算法3次之.